Table of Contents |
Population is the group of a given species in a specific time and area. Population ecology is the study of those populations, their characteristics, their growth, and what influences that growth. The following are the important characteristics and what they mean.
Population growth is the rate of growth of a species over a period of time. Population growth is usually understood through modeling or the following simple equation:
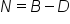
In this formula,
Positive growth rate occurs when there are more births than deaths. Negative growth occurs when there are more deaths than births, and zero change occurs when the two are equal.
IN CONTEXT
Let's calculate the fictional population growth of rabbits in Cottonwood, as shown in the graph below.
The initial population was 50. Suppose in the first year, there were 20 births and five deaths; 20−5=15. Therefore, the population change was +15.
You can see that the total population changed from 50 to 65 in 2001, which is an increase of 15.
This process was continued until 2004. The "N", or population change, for 2002 was 25. In 2003, it was zero, and in 2004, it was 25 again.
Within the study of population growth, there are two main types: exponential and logistic.
Exponential growth assumes unlimited resources in an idealized situation without limiting factors. Because of this assumption, the population can grow in an exponential manner based on birth and death rates. However, in the real world, exponential growth cannot be sustained for long in any population.
An exponential growth curve, with time on the x-axis and population on the y-axis, is a lot like the shape of the letter “J” (shown in the diagram below) when extended over time. The slope of an exponential population graph at any given interval is determined by the rate of change in births and deaths.

EXAMPLE
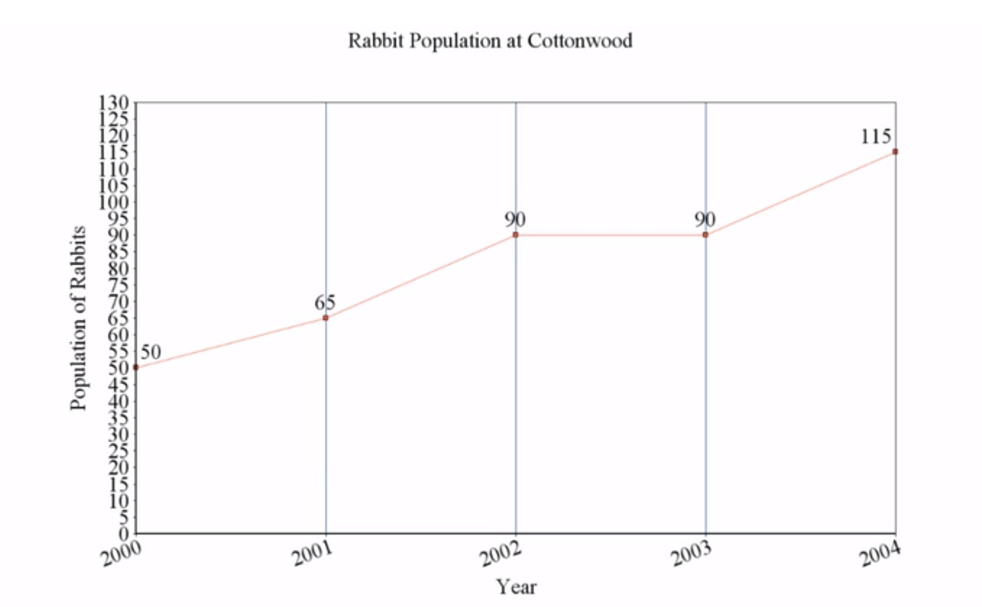
The first graph below shows a shallower growth curve because the population has a lower birth rate. However, if that birth rate increases, the curve of the graph will get steeper.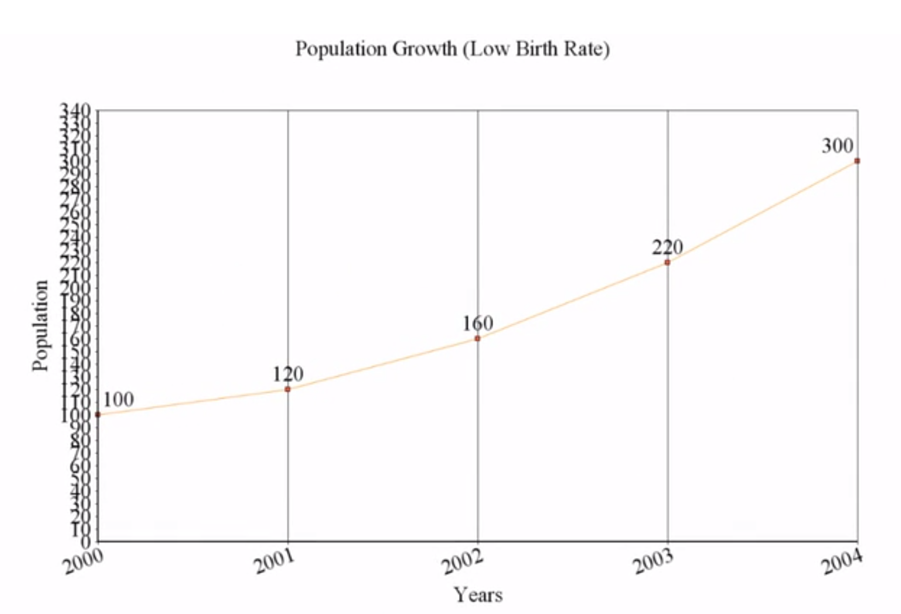
EXAMPLE
Next, we have another graph. The data here is the same, except that the birth rate is higher. Can you see how the curve of the graph is steeper? Even though infinite exponential growth is unrealistic, it gives scientists the ability to understand the maximum potential population growth in ideal conditions for a species.
On the other, more realistic side of things is a logistic population growth graph, which takes into account limited available resources. Limiting factors can be either biotic, such as food availability, or abiotic, such as the amount of precipitation.
Because of limiting factors, all populations in a certain area have a carrying capacity, also referred to as K. Carrying capacity is the maximum sustainable population that an area can support. If a population exceeds this benchmark, it will inevitably decrease and fall below this line, because the ecosystem cannot support anything above that line.
EXAMPLE
Consider the graph below. Note the dotted line representing the carrying capacity, or K. Logistic graphs tend to create an S-curve as the population's growth rate increases and then, as it nears K, decreases. In ecosystems, species populations are generally below the carrying capacity for that species in that location.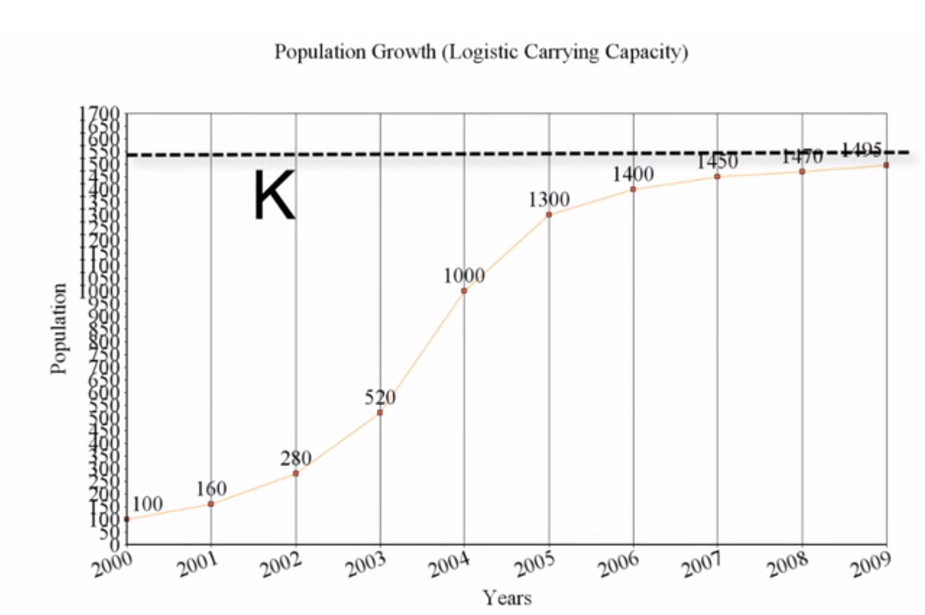
Another important tool for population ecologists is the life table. Life tables, like the one below, summarize age-specific birth and death rates for a species population.
| Life Chart of a Fictional Insect | ||
|---|---|---|
| Age (Months) | Number Alive | Fecundity |
| 0 | 843 | 0 |
| 1 | 722 | 300 |
| 2 | 527 | 620 |
| 3 | 316 | 430 |
| 4 | 144 | 210 |
| 5 | 54 | 60 |
| 6 | 15 | 30 |
| 7 | 3 | 10 |
| 8 | 0 | |
This table shows the number of fictional insect species at various ages. At 1 month, it has dropped down to 722 individuals. Its birth rate at 3 months is 430.
Life tables like these are used for population management and conservation. It allows us to identify the parts of species populations at specific times that need protection or that can be harvested.
Source: THIS TUTORIAL WAS AUTHORED BY JENSEN MORGAN FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.