Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Piecewise Functions and Their Graphs

Author: Sophia
PDF Version

what's covered
In this lesson, you will graph piecewise functions. Specifically, this lesson will cover:

Table of Contents

1. Graphing a Function on a Restricted Domain

When we graph a function, we are considering the entire function. What if we only wanted part of the graph?

EXAMPLE

Consider the function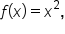 f open parentheses x close parentheses equals x squared comma and several “pieces” of the graph, as shown below:

Graph 1: bold italic f open parentheses bold x close parentheses bold equals bold italic x to the power of bold 2 (entire graph) Graph 2: bold italic f open parentheses bold x close parentheses bold equals bold italic x to the power of bold 2 bold comma bold space bold italic x bold greater or equal than bold 1
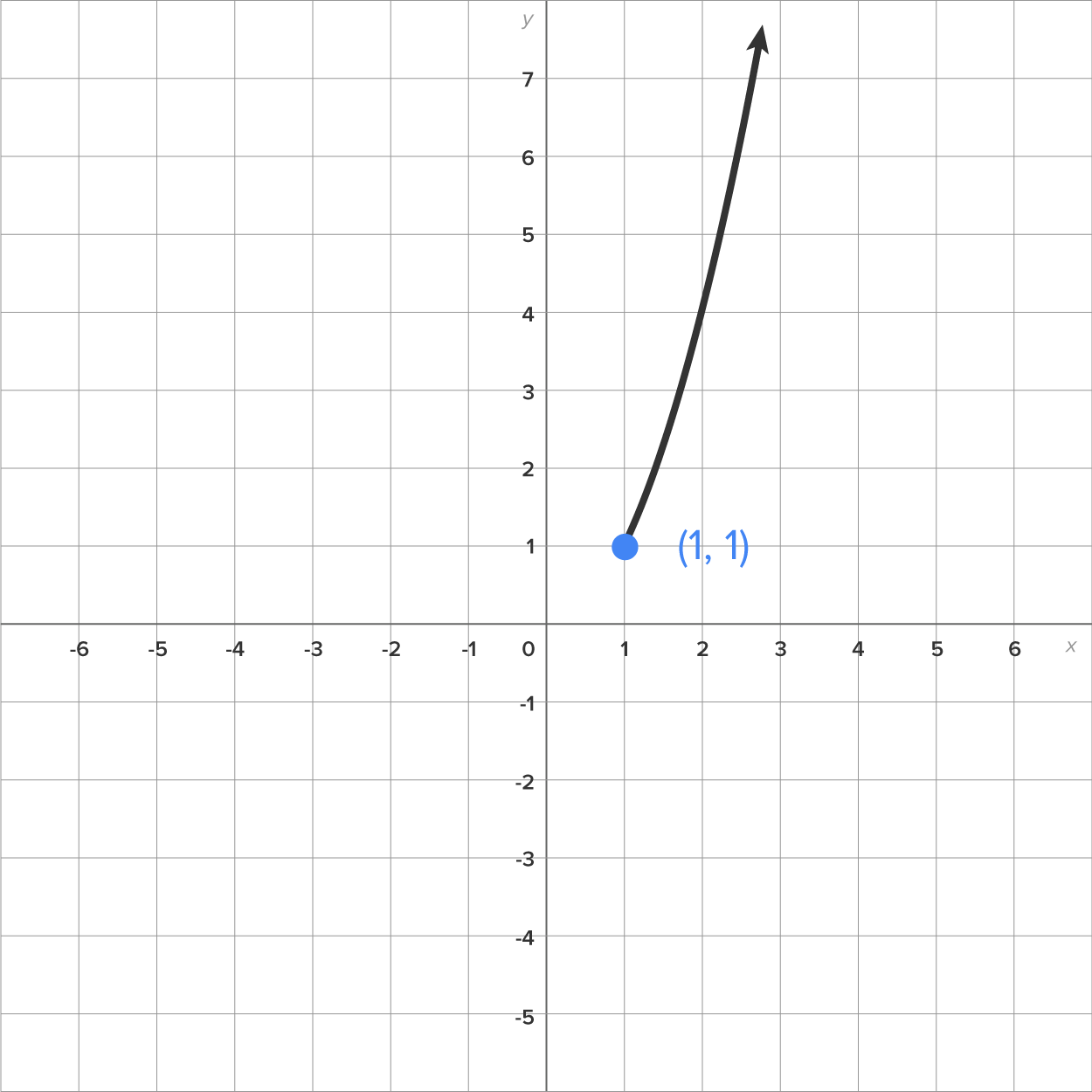
A graph with an x-axis ranging from – 6 to 6 and a y-axis ranging from –5 to 7. A parabola descends from the second quadrant, reaches a minimum at the point (0, 0), and then rises in the first quadrant. A graph with an x-axis ranging from – 6 to 6 and a y-axis ranging from –5 to 7. A curve starts from a marked point at (1, 1) and rises in the first quadrant.
Graph 3: bold italic f open parentheses bold x close parentheses bold equals bold italic x to the power of bold 2 bold comma bold space bold short dash bold 1 bold less or equal than bold italic x bold less than bold 2 Graph 4: bold italic f open parentheses bold x close parentheses bold equals bold italic x to the power of bold 2 bold comma bold space bold italic x bold less or equal than bold 0
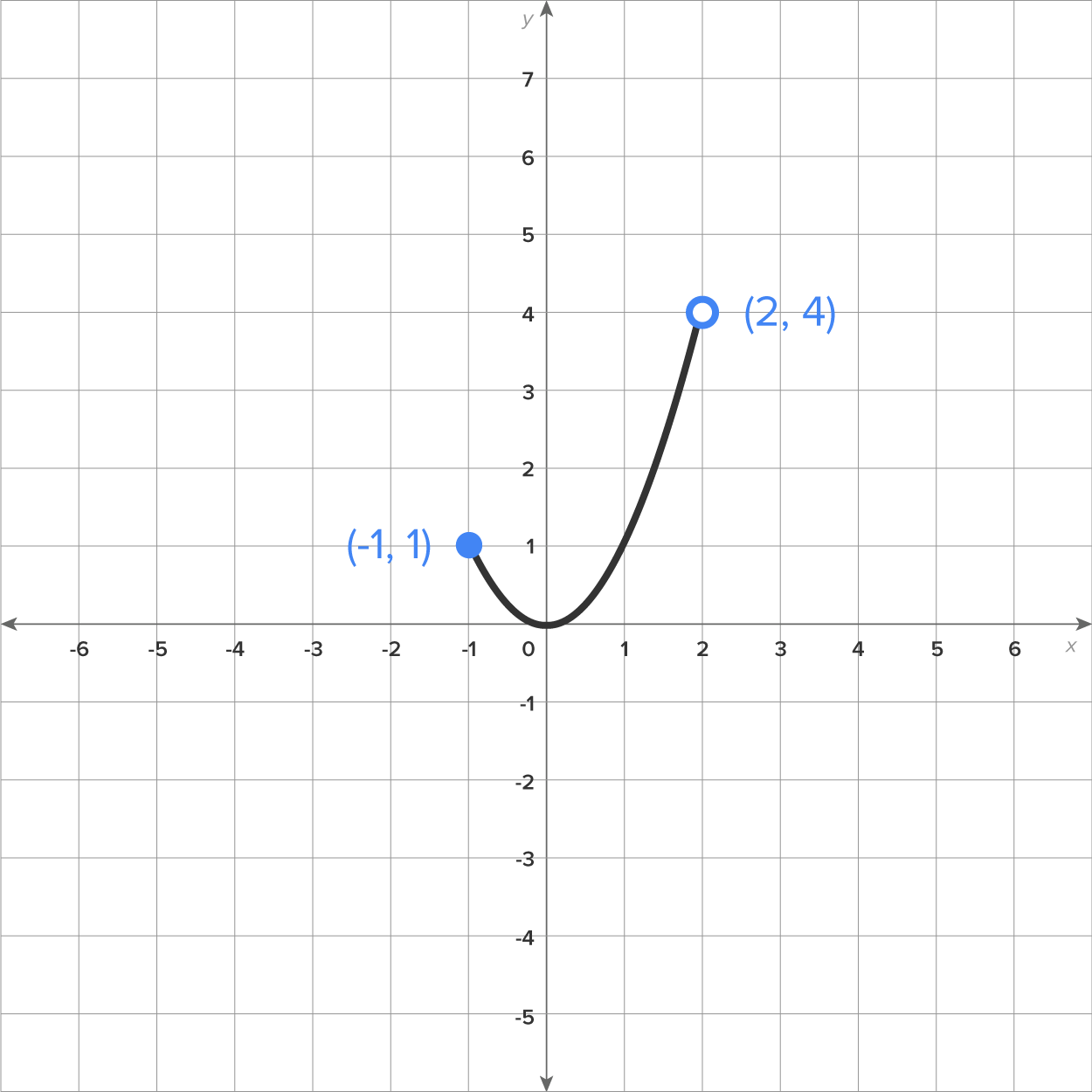
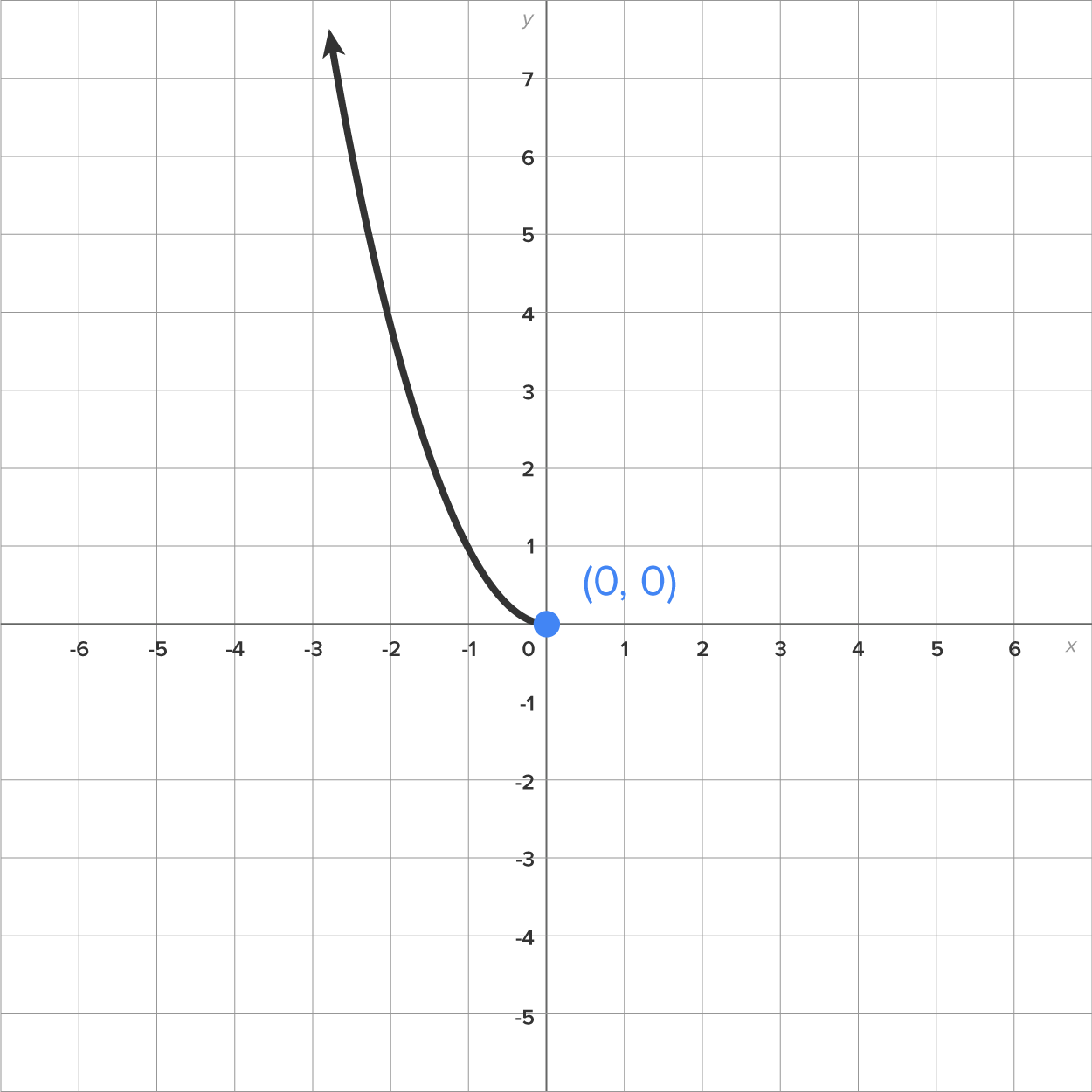
A graph with an x-axis ranging from – 6 to 6 and a y-axis ranging from –5 to 7. A portion of a parabolic curve descends from a filled dot at (–1, 1), reaches a minimum at the point (0, 0), then rises in the first quadrant unmtil reaching an open circle at (2, 4). A graph with an x-axis ranging from – 6 to 6 and a y-axis ranging from –5 to 7. A portion curve rises to the left from the marked point at (0, 0), passes through the points (-1, 1) and (-2, 4), then continbues to rise in the second quadrant.

To sketch a portion of the graph, a restricted domain is used. Recall that the domain of a function is the set of all possible inputs for a function.

For instance, in Graph 3 above, the 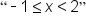“ short dash 1 less or equal than x less than 2 ” is the domain restriction since it is not the entire domain of 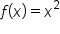f open parentheses x close parentheses equals x squared (which is all real numbers).

hint
When an endpoint is included, we represent it by using a closed circle. See Graphs 2, 3, and 4.

When an endpoint is not included, we represent it by using an open circle. See Graph 3.

try it
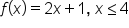
Consider the following function: f open parentheses x close parentheses equals 2 x plus 1 comma space x less or equal than 4
Graph this function.
Remembering that y equals 2 x plus 1 is a line with slope 2 and y-intercept 1, we graph the line but only for values of x up to and including 4.

A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10. A line starts at the marked point at (4, 9), passes through the points (0, 1) and (−0.5, 0), and extends into the third quadrant.

term to know
Restricted Domain
Part of, but not the entire, domain of a function.

2. Graphing a Piecewise Function

A piecewise function is made up of other functions that are on restricted domains. For instance, consider the function:

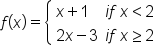
f open parentheses x close parentheses equals open curly brackets table attributes columnalign left center end attributes row cell x plus 1 end cell cell i f space x less than 2 end cell row cell 2 x minus 3 end cell cell i f space x greater or equal than 2 end cell end table close

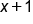The function tells us to use “x plus 1”, but only if the input is less than 2, and to use “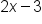2 x minus 3” if the input is at least 2.

This means that the graph of the function will be “part of” the graph of 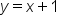y equals x plus 1 along with “part of” the graph of 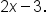2 x minus 3. Here is how we put this together:

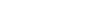
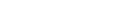
bold italic y bold equals bold italic x bold plus bold 1 bold comma bold space bold italic x bold less than bold 2 bold italic y bold equals bold 2 bold italic x bold minus bold 3 bold comma bold space bold italic x bold greater or equal than bold 2
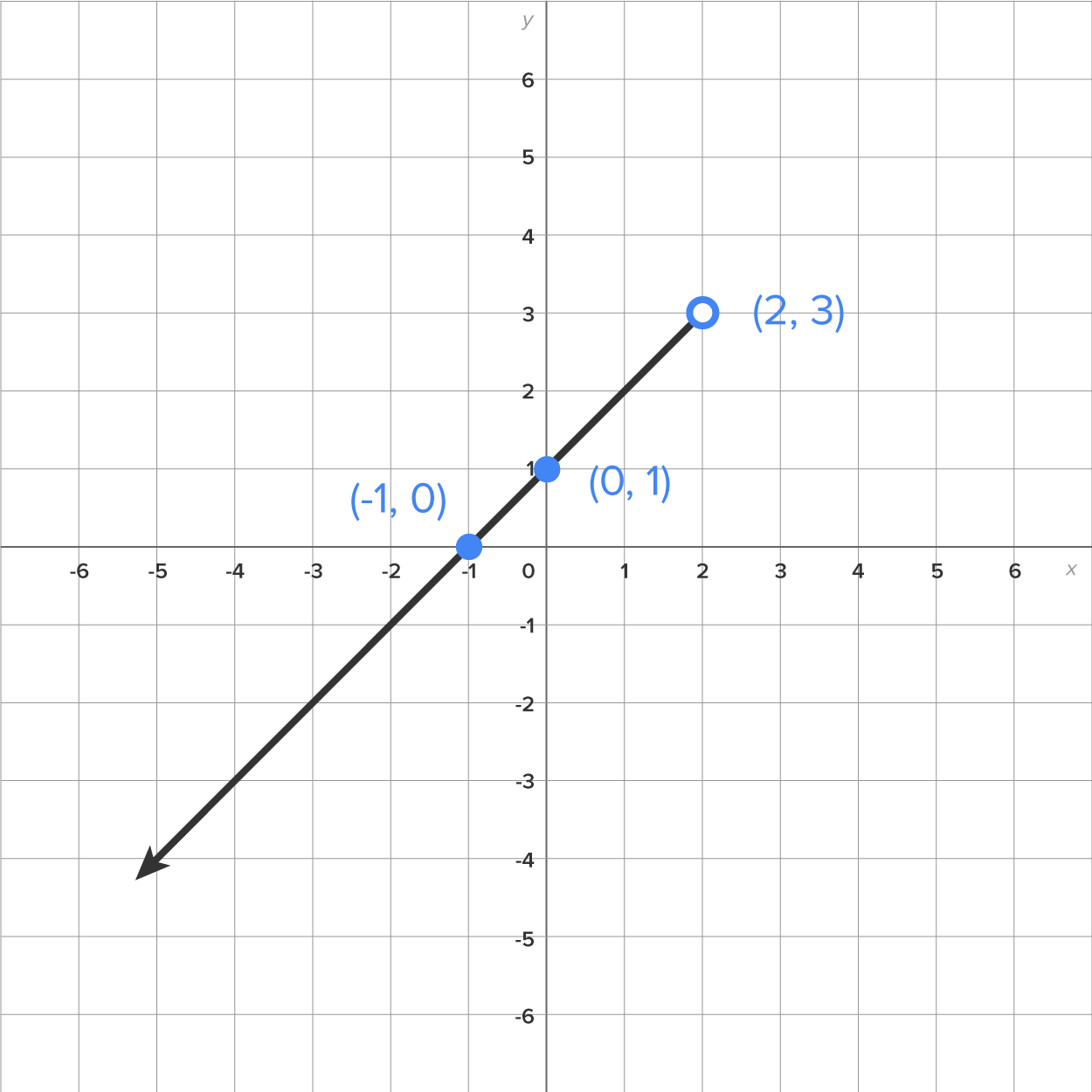
A graph with an x-axis and a y-axis ranging from −6 to 6. A line starts at an open circle at (2, 3), passes through the filled dots at (0, 1) and (−1, 0), and extends into the third quadrant. A graph with an x-axis and a y-axis ranging from −6 to 6. A line rises from a marked point at (2, 1), passes through the point (3, 3), and extends upward.

The graph of f open parentheses x close parentheses is these pieces put together on one graph as follows:

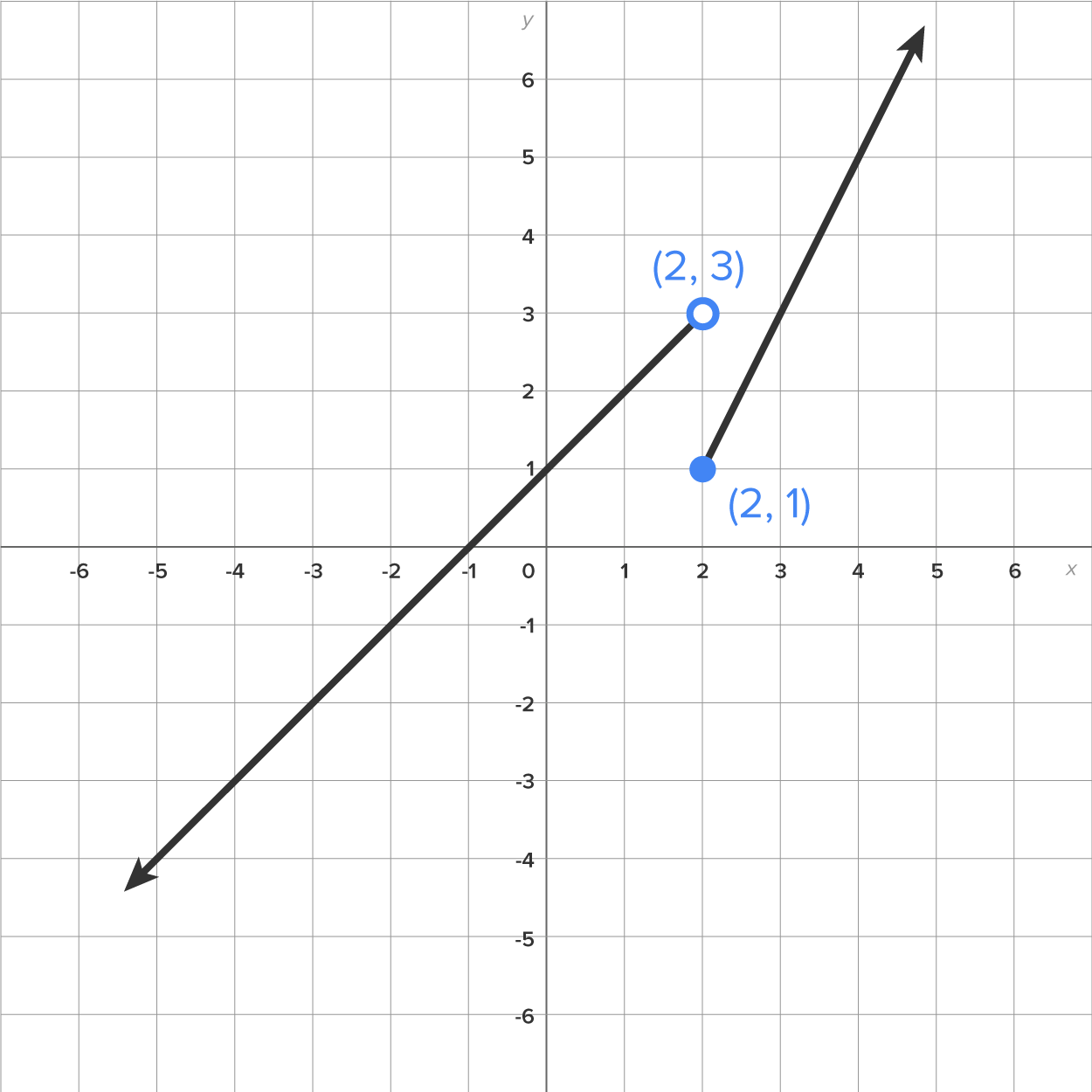
A graph with an x-axis and a y-axis ranging from −6 to 6. The graph consists of two slanting lines with a restricted domain. The first line rises from the third quadrant, passing through the points (-1, 0) and (0, 1), then ending at an open circle at (2, 3).The second line slants upward from a filled dot at (2, 1), passes through the point (3, 3), and extends upward.

hint
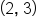In the previous graph, notice that there is an open circle at open parentheses 2 comma space 3 close parentheses and a closed circle at 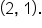open parentheses 2 comma space 1 close parentheses. If both circles were closed, then the graph would not represent a function. A common error is to close both circles at the breaking point, so be sure to double check which one is included and which one is not, since both cannot be included!

watch
The following video walks you through the process of graphing a piecewise function.

summary
In this lesson, you learned that in cases where you want to sketch only a part of a graph, you would graph a function on a restricted domain, which is part of (but not the entire) domain of a function. You also learned how to graph a piecewise function, which is the result of bringing together the graphs of each piece of the function over the respective restricted domains.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM 1) CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES. 2) OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

Terms to Know
Restricted Domain

Part of, but not the entire, domain of a function.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.