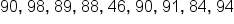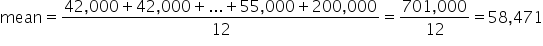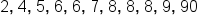In this lesson, we will discuss how extreme data can affect measures of center and therefore potentially throw off your interpretation of the data. We will also take a deeper dive into strengthening your results driven skill by analyzing data. Specifically, this lesson will cover:
1. Outliers
When analyzing a data set, it is common to have some numbers that aren’t especially close to others. It is important to look for outliers, which are not just the highest or lowest numbers, but are numbers that are very far above the next highest number in the data set or very far below the next lowest number in the data set.
-
EXAMPLE
Suppose that a small class took an exam, and the scores were as follows:
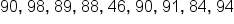
Some students did very well on this test. In fact, most students scored in the 80's or the 90's. However, one person scored only 46. That 46 would be considered an outlier because it's so much lower than the rest of the pack.
-
Whenever you are analyzing a set of data, it is often helpful to write the data in ascending order. This is already required to find the median, but also makes it easier to identify patterns in the data as well as outliers.
-
Outliers are important data points because they are so high or low that they would be considered unusual.
-
- Outlier
- A point in a data set that is so high or so low as to be unusual, given the rest of the values.
2. Effect of Outliers on Measurements of Center
It is common for large data sets to have outliers. Because of this, you may encounter situations in which the mean is not the best representation of the center of the data.
-
EXAMPLE
Suppose that you have 12 employees. Eight of them are shift workers, three of them are managers, and there’s one boss. Here are the salaries for the respective positions:
-
Shift Worker: $42,000, $42,000, $42,000, $42,000, $42,000, $42,000, $42,000, $42,000
-
Manager: $55,000, $55,000, $55,000
-
Boss: $200,000
Calculate the mean of the eight shift workers, the three managers, and the boss.
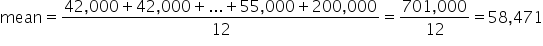
Here the mean of the 12 workers is over $58,000. However, eleven of the 12 employees make less than $58,000, and only one makes more than that (and makes substantially above that amount). Therefore, it doesn't really make a lot of sense to use the mean as a measure of center for this data set because this number does not represent the center of the data well. The boss’s $200,000 salary is considered an outlier in this data set. This is why historically, determining the average income of a population, or even a company, is not typically done alone. Because of this, other measures of center are used as well—such as the median and mode.
-
In the presence of outliers, which are extremely high or extremely low values, the mean won't give an accurate representation of center. Generally, the median is used in the presence of outliers.
We have seen that the mean is affected by outliers. How is the median affected by extreme values? Suppose that you have another 10-point quiz for a different class of 11 students. Here are the scores, in order:
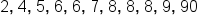
The median for this set of data is 7.
Obviously, one of these values, 90, is completely out of range. Maybe that’s because of a typo? We can't be sure. Despite this potential typo, however, the median of this data set is 7 because that is the middle number. If you correct the typo, changing that 90 to a 9, for instance, the median will still be 7.
-
The median is not overly affected by outliers or extreme values.
Obviously, there are a few options to use to determine the measure of center for a group of data. But when should you use each in your daily life? When should you use a mean to understand your data? In short, the mean is the default measurement that you should use if there are no outliers. It is the best measurement to use if possible because it's the most versatile measure of center and therefore the most appropriate one in most cases.
So, when should you use the median to understand your data? While the mean is typically the go-to for data consumption, if there are outliers present in the data set, the median is the best option for the measure of center.
Ultimately, it is recommended to have the mean, median, mode, and range determined to truly understand the data. When reading current events that give only one of these values, make sure to ask yourself why only one was given. Is the author choosing the value that best matches their point of view? Were they simply lazy? Always make sure to do your due diligence and come to your own conclusion. We’ll talk more about this in a later lesson.
Imagine you have a goal to run a 5K and finish in the top 10%. You analyze the finishing times for the runners of the previous years. Using your knowledge of mean, median, mode, and outliers, what steps would you take to determine how fast you’ll need to run to meet your goal? What other factors should you examine when looking at this data?
In this lesson, you learned how outliers can affect measurements of center and which of these measures should be used in each circumstance in your daily life. In general, do not trust sources that only provide one measurement of center.
Best of luck in your learning!