In this lesson, you will define and explore the order of operations. You will also see how this applies to problem solving skills in your every day life. Specifically, this lesson will cover:
1. Importance of the Order of Operations
Have you ever seen something like this in your social media feed with the challenge to solve it?
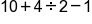
What is the answer? Is it 11? 6? 14? You see multiple different answers given and everyone insists they have the right answer. Why is that?
Well, in math, an operation is a way to combine numbers, as in addition or multiplication. You can think of an operation in math as a calculation between two or more numbers.
There needs to be an agreed upon order for performing operations so that when there are several operations in an expression or an equation, everyone simplifies or solves in the same way to get the correct answer. Therefore, the order of operations is the rule that tells you the order in which to perform those operations.
The correct order of operations is Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction, otherwise referred to by the acronym PEMDAS.
-
Want an easy way to remember “PEMDAS”? Create a phrase that can help you remember such as:
Please
Excuse
My
Dear
Aunt
Sally. You can use this phrase or come up with one of your own!
-
- PEMDAS
- An acronym used to remember the order of operations: parentheses, exponents, multiplication, division, addition, subtraction.
2. PEMDAS
PEMDAS is the acronym you can use to remember the order of operations. PEMDAS stands for:
- Parentheses
- Exponents
- Multiplication and Division
- Addition and Subtraction
There are several important things to remember when using PEMDAS:
- Parentheses
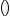 include other grouping symbols, such as brackets
include other grouping symbols, such as brackets 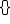 or radical signs
or radical signs 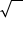 .
.
- Multiplication and division are performed together from left to right in the order that they appear.
- Similarly, addition and subtraction are performed together from left to right in the order that they appear.
-
Think of each part of PEMDAS as a “level.” First, scan the expression for any parentheses. If there are any, complete all of the operations inside before moving on to the next level. At the next level, complete all multiplication and division sections (from order of left to right). Once that is solved, move on to addition and subtraction (from order of left to right).
You can use the order of operations to simplify an expression.
-
EXAMPLE
Suppose you want to simplify the expression:
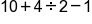
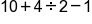
|
The expression
|
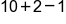
|
Since there are no parentheses, you can move to the next level and start with division; divide 4 by 2.
|
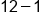
|
Now that the multiplication/division level is complete, only the addition and subtraction operations are remaining. Because these are on the same level, complete the addition and subtraction operations from left to right; first, add 10 and 2.
|
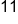
|
Find the solution by subtracting 1 from 12.
|
If this had been on your social media feed, and one of your friends solved the expression without using the proper order of operations, they may have just tried to solve it from left to right. If they would have done that, they would start with 10 plus 4, which equals 14; 14 divided by 2 is 7, and 7 minus 1 is 6, which is an incorrect answer.
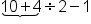
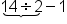
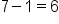
This is why you find so many incorrect answers to these social media challenges. You can see that without having a standard order of operations, you can potentially arrive at many different answers with everyone insisting they are correct.
-
Suppose you have the following expression:

.
3. Common Mistakes
Before we move on, it is important to note a common mistake that people make when solving or simplifying expressions containing negative numbers and exponents. Consider the two similar, but different, equations or statements below:
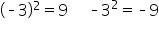
- In the first equation, you have negative 3 in parentheses squared, which equals a positive 9. Negative 3 squared means negative 3 times negative 3, which is a positive 9.
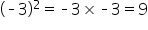
- In the second equation, you have a negative 3 squared, which equals negative 9. That’s because the negative here is like a negative 1 being multiplied by the 3 squared. Therefore, the answer becomes negative 9.
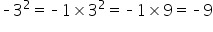
Now that you know how to avoid this common mistake, try using this knowledge when solving the equation in the second example.
-
Many people think that algebra skills are not applicable in everyday life; however, we frequently use algebraic concepts to solve problems without even realizing it—even outside of finding correct answers on social media posts! For instance, if you go to a store and you want to buy two pairs of jeans that cost $20 each, as well as a belt that costs $10, you will need to use order of operations to accurately determine the total cost. In this case, the problem is 2 X 20 + 10. By using the correct order of operations, you know that you have to multiply first (2 X 20), which is $40. You then add $10, making the total $50. If you had added before multiplying, you would incorrectly determine that the total cost is $60.
Today you learned about the importance of the order of operations, which lets us simplify expressions and equations to find the correct answer. You also learned the acronym PEMDAS to remember the order of operations, noting that multiplication and division, as well as addition and subtraction, are performed together from left to right in the order that they appear. Finally, you learned a common mistake occurs when there are negatives. When raising a negative number to an exponent, parentheses must be used around the negative sign as well.
Best of luck in your learning!
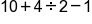
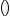 include other grouping symbols, such as brackets
include other grouping symbols, such as brackets 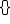 or radical signs
or radical signs 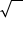 .
. 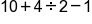
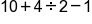
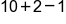
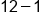
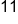
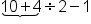
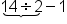
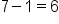
 .
.
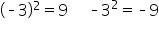
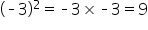
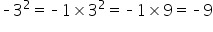
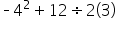 .
.