Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

One to One Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to identify the graph of a one-to-one function. Specifically, this lesson will cover:

Table of Contents

1. Function Review

A defining characteristic of a function is that for every element in the domain/input, there is exactly one corresponding element in the range/output. If we look at this graphically, we we will see that the graph of a function passes the Vertical Line Test, where a vertical line is drawn, and if the graph does not touch the line in more than one place we consider this a function.

A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −5 to 6. It consists of a parabola opening upward and three vertical dashed lines. The parabola descends from the second quadrant, passes through the point (−1.8, 0), reaches s minimum at the point (0, −3), and then rises into the fourth quadrant to extend further into the first quadrant by passing through the point (1.8, 0). One vertical dashed line, x equals −3, extends from the second quadrant to the third quadrant, passing through the points (−3, 6) and (−3, 0). The second vertical dashed line, x equals 5, extends from the first quadrant to the fourth quadrant. The third vertical dashed line, y equals 0, overlaps with the y-axis.

big idea
Notice how the graph does not touch each vertical line more than once. When this occurs, we say that the graph represents a function. What this means that is that each input, or x-value, of the function corresponds to exactly one output, or y-value which is the same as an f open parentheses x close parentheses value.

2. Introduction to One-to-One Functions

One-to-One functions are special types of functions where every value in the domain of the function corresponds to only one value in the range and each value in the range corresponds to only one value in the domain.

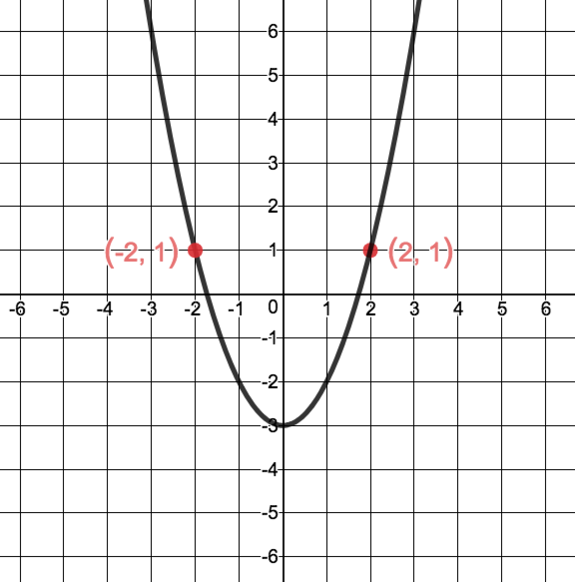
Notice that in the graph shown above, the function is NOT a one-to-one function. This is because there is at least one instance where two or more x-values result in the same y-value, for example (-2, 1) and (2, 1).

A graph with an x-axis and a y-axis ranging from −6 to 6. It consists of a parabola opening upward. The parabola descends from the second quadrant, passes through the marked point (−2, 1) and the point (−1.8, 0), reaches a minimum at the point (0, −3), and rises into the fourth quadrant to extend further into the first quadrant, passing through the point (1.8, 0) and the marked point (2, 1).

3. Determining if a Function is One-to-One

In order to determine if a function is one-to-one we can use two methods:

  • Graphically, where we perform both a Vertical Line Test and a Horizontal Line Test.
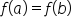  • Algebraically, where we use two values a and b to find f open parentheses a close parentheses equals f open parentheses b close parentheses and manipulate the problem to show that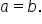 a equals b.

3a. Graphically

Given a graph of a function, we can simply draw vertical and horizontal lines on the graph to help determine if the graph represents a one-to-one function. If the graph only touches each line once then we may be safe in saying that the graph represents a one-to-one function.

In a Horizontal Line Test, horizontal lines are drawn on the coordinate plane and we try to determine how many times the graph of a function touches each horizontal line. If the graph only touches each horizontal line once we say that the graph passes the Horizontal Line Test.

EXAMPLE

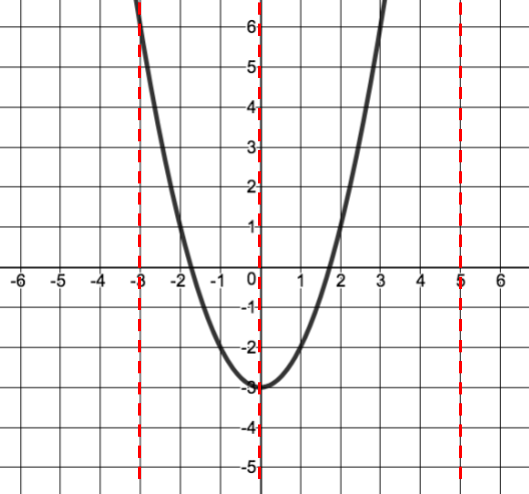
Determine if the following graph is one-to-one.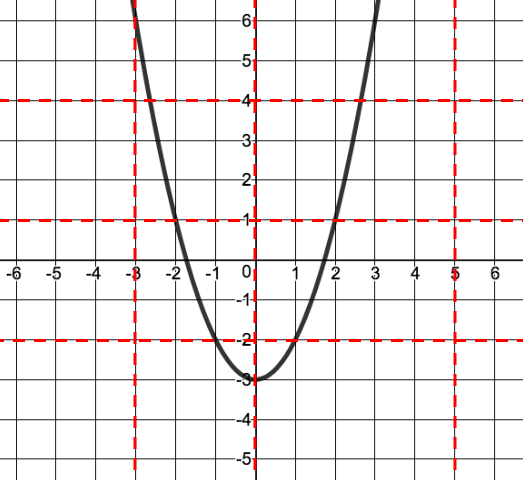

A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −5 to 6. It consists of a parabola opening upward, three vertical dashed lines, and three horizontal dashed lines. The parabola descends from the second quadrant, passes through the point (−1.8, 0), reaches a minimum at the point (0, −3), and then rises into the fourth quadrant to extend further into the first quadrant, passing through the point (1.8, 0). One vertical dashed line passes through x equals −3 and extends from the second quadrant to the third quadrant. The second vertical dashed line passes through x equals 5 and extends from the first quadrant to the fourth quadrant. The vertical dashed line, y equals 0, overlaps with the y-axis. The three horizontal dashed lines are located at y equals −2, y equals 1, and y equals 4, which extend from left to right across the grid.

Although it passes the Vertical Line Test, this graph does not pass the Horizontal Line Test, so this graph does not represent a one-to-one function.

EXAMPLE

Determine if the following graph is one-to-one.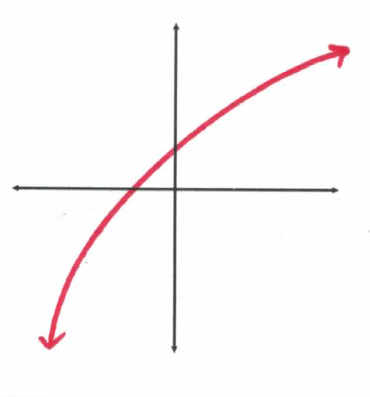

A graph with two axes intersecting at right angles, namely, the x-axis and the y-axis. It is an increasing curve that opens rightward. It rises from the third quadrant and passes through the negative x-axis and positive y-axis to further ascend into the first quadrant. The graph suggests a curve that is not parabolic.

This function is one-to-one because it passes both the vertical and horizontal line tests.

big idea
If a graph passes both the Vertical and Horizontal Line Tests, then the graph represents a one-to-one function.

3b. Algebraically

Sometimes a graph of a function may be too large to draw on a coordinate plane so it can be difficult to determine if the graph represents a one-to-one function. In such cases, is it better to determine if a function is one-to-one algebraically. To determine if a function is one-to-one algebraically we do the following:

step by step
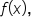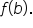
  1. Given a function f open parentheses x close parentheses comma use two values a and b to find f open parentheses a close parentheses and f open parentheses b close parentheses.
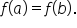
  2. Assume f open parentheses a close parentheses equals f open parentheses b close parentheses.
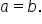
  3. Manipulate the problem to show that a equals b.

If we can prove that 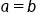a equals b, then the function is one-to-one.

EXAMPLE

Determine if the function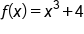 f open parentheses x close parentheses equals x cubed plus 4 is one-to-one.

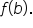
First, we use two values a and b to find f open parentheses a close parentheses and f open parentheses b close parentheses.

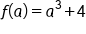
f open parentheses a close parentheses equals a cubed plus 4
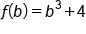
f open parentheses b close parentheses equals b cubed plus 4

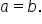
Next, we set them equal to each other and then manipulate the problem to see if a equals b.

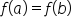
f open parentheses a close parentheses equals f open parentheses b close parentheses Substitute expressions for 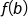f open parentheses a close parentheses and f open parentheses b close parentheses
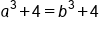
a cubed plus 4 equals b cubed plus 4 Subtract 4 from both sides
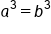
a cubed equals b cubed Take cube-root of both sides
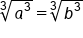
cube root of a cubed end root equals cube root of b cubed end root Simplify
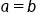
a equals b Our solution

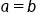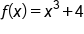Since we were able to get a equals b, the function f open parentheses x close parentheses equals x cubed plus 4 is one-to-one.

hint
By knowing the type of function, we can automatically tell (without graphing) whether it is one-to-one.

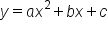  • The graph of a quadratic function y equals a x squared plus b x plus c is never one-to-one. You can always find a horizontal line that passes through two points.
Lines, however, offer a bit more variety.

  • If a line has either a positive or negative slope, then it is a one-to-one function.
  • If the linear function has zero slope (a horizontal line), then it is NOT one-to-one.
  • Vertical lines violate the condition of being a function, which means that vertical lines cannot be one-to-one functions.

EXAMPLE

Without graphing, we know the following:

Equation One-To-One Function? Reasoning
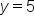
y equals 5 No Horizontal Line
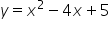
y equals x squared minus 4 x plus 5 No Parabola
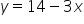
y equals 14 minus 3 x Yes Line with negative slope
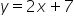
y equals 2 x plus 7 Yes Line with positive slope
x equals 4 No Not a function

summary
Reviewing functions, recall that a defining characteristic of a function is that for every element in the domain/input, there is exactly one corresponding element in the range/output. One-to-One functions not only pass the Vertical Line Test, but they also must pass the Horizontal Line Test. We can determine if a function is one-to-one graphically by looking at using these tests, Passing the Vertical Line Test means that there's exactly one value for y at any given x value and passing the Horizontal Line Test means that there's exactly one value for x at any given y value. 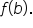To determine if a function is one-to-one algebraically, we need to test to see if a equal b if f open parentheses a close parentheses equal f open parentheses b close parentheses.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.