Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

One-Tailed and Two-Tailed Tests

Author: Sophia
PDF Version

what's covered
This tutorial will cover the difference between a one-tailed and a two-tailed test in a hypothesis test. Our discussion breaks down as follows:

Table of Contents

1. One-Tailed Test

A one-tailed test is a test for when you have reason to believe the population parameter is higher or lower than the assumed parameter value of the null hypothesis.

One-tailed tests have two versions:

  • Right-tailed test
  • Left-tailed test
term to know
One-Tailed Test
A test for when you have reason to believe the population parameter is higher or lower than the assumed parameter value of the null hypothesis.

1a. Right-Tailed Test

A right-tailed test is a type of one-tailed test that means that the alternative hypothesis is larger than the claimed parameter.

IN CONTEXT

Suppose you have your favorite soda, Liter O'Cola, and it's come out with new Diet Liter O'Cola. They think that it's indistinguishable from their regular cola, so they obtain 120 individuals to do the taste test. If the claim is true, you would expect around 60 people, which is 50%, would guess correctly, simply based on guessing, even if the diet cola was indistinguishable from the classic cola.

However, what if some people can taste the difference? What would you expect the proportion of people correctly selecting the diet cola to be? You would likely say that it's some number over 50%. At least half of the people will be able to correctly identify which cup is the diet cola.

You could make the following null and alternative hypotheses:

begin mathsize 18px style table attributes columnalign left end attributes row cell H subscript 0 colon space p equals 0.50 semicolon space H a l f space o f space t h e space p e o p l e space w i l l space b e space a b l e space t o space s e l e c t space t h e space d i e t space c o l a. end cell row cell H subscript a colon space p greater than 0.50 semicolon space O v e r space h a l f space o f space t h e space p e o p l e space w i l l space b e space a b l e space t o space s e l e c t space t h e space d i e t space c o l a. end cell end table end style

Your null hypothesis says that p, the true proportion of people who can correctly identify the diet cola, is 1/2, or half the people. Your alternative hypothesis suspects that maybe more than half of people will be able to select the diet cola correctly.

Since you're only interested in testing whether or not the true proportion of people who can guess correctly or identify which one is the diet cola is over half, this will be considered a right-tailed test—a specific type of a one-tailed test. You don't care if it's under half. If it's under half, that actually works in Liter O'Cola's favor.

The distribution of a right-tailed test would look similar to the following curve:

Right-tailed test

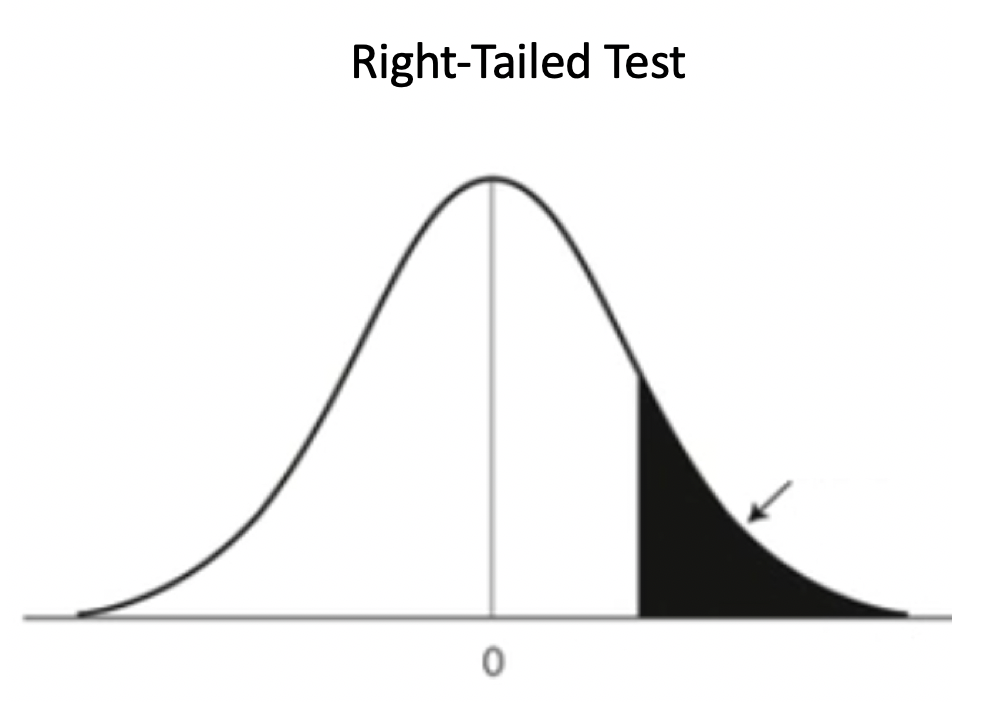
We are looking at the values higher than the assumed value, which is the section to the right of this value.

term to know
Right-Tailed Test
A hypothesis test where the alternative hypothesis only states that the parameter is higher than the stated value from the null hypothesis.

1b. Left-Tailed Test

A left-tailed test is a type of one-tailed test in which the alternative hypothesis claims that it's less than the claimed parameter.

IN CONTEXT

Suppose you suspect that Liter O'Cola is under-filling their bottles. Unsurprisingly, the bottles are supposed to contain one liter of cola.

State the null and alternative hypotheses for this.

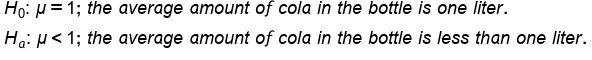
begin mathsize 18px style table attributes columnalign left end attributes row cell H subscript 0 colon space mu equals 1 semicolon space t h e space a v e r a g e space a m o u n t space o f space c o l a space i n space t h e space b o t t l e space i s space o n e space l i t e r. end cell row cell H subscript a colon space mu less than 1 semicolon space t h e space a v e r a g e space a m o u n t space o f space c o l a space i n space t h e space b o t t l e space i s space l e s s space t h a n space o n e space l i t e r. end cell end table end style

This is another example of a one-tailed test, more specifically, a left-tailed test. The null hypothesis says that the average amount of cola in the bottle is one liter for all the bottles that Liter O'Cola makes. The alternative is that perhaps it's less than one liter—they're under-filling the bottles. The average amount is less than one liter.

If the average amount, μ, was greater than one liter, you wouldn't really have a claim against Liter O'Cola because you're actually getting more soda than they claim they're providing. You're only going to give them trouble if they're under-filling their bottles.

The distribution of a left-tailed test would look similar to the following curve:

Left-tailed test

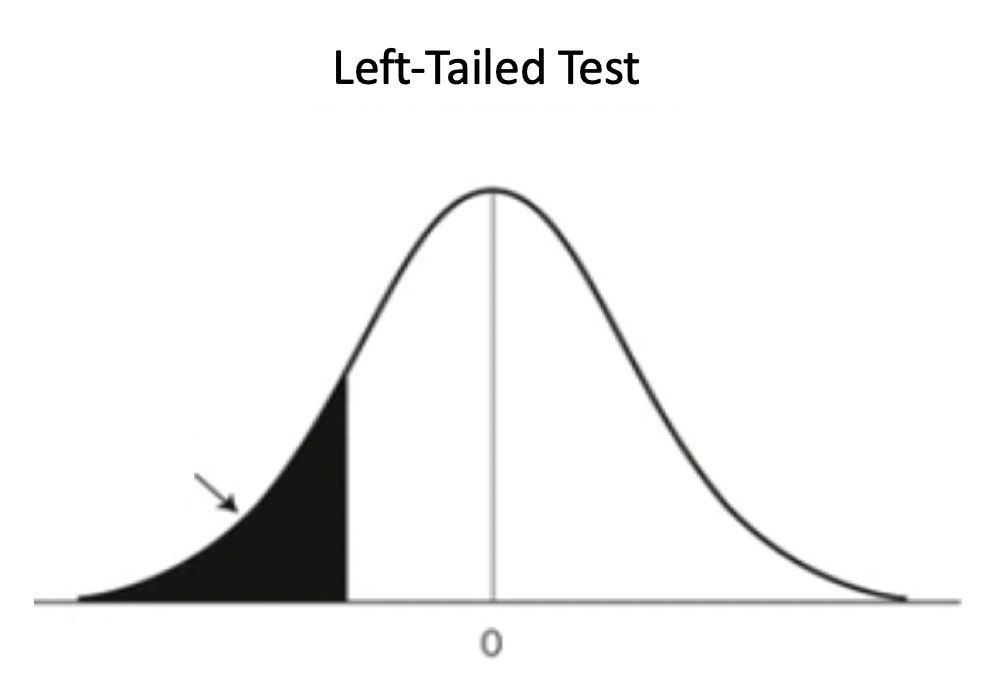
We are looking at the values lower than the assumed value, which is the section to the left of this value.

term to know
Left-Tailed Test
A hypothesis test where the alternative hypothesis only states that the parameter is lower than the stated value from the null hypothesis.

2. Two-Tailed Test

A two-tailed test is when we have reason to believe the population is different from the assumed parameter value of the null hypothesis.

IN CONTEXT

Liter O'Cola also claims there are 35 grams of sugar in its bottles of cola. Anything over that and the soda will taste too sweet. Anything under that and the soda won't taste quite sweet enough. Consumers won't get the refreshing Liter O'Cola taste that they have come to expect. We suspect that Liter O'Cola might have altered their formula recently because it tastes differently.

What do you think the null and alternative hypotheses will be here with respect to sugar?

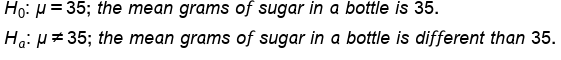
begin mathsize 18px style table attributes columnalign left end attributes row cell H subscript 0 colon space mu equals 35 semicolon space t h e space m e a n space g r a m s space o f space s u g a r space i n space a space b o t t l e space i s space 35. end cell row cell H subscript a colon space mu not equal to 35 semicolon space t h e space m e a n space g r a m s space o f space s u g a r space i n space a space b o t t l e space i s space d i f f e r e n t space t h a n space 35. end cell end table end style

Here, the null hypothesis is that the mean grams of sugar will be the same as it was before, 35.

What about the alternative hypothesis? Well, if they've changed their formula, you don't know if they added more sugar or put in less sugar. However, they're only going to be in trouble if they put in a different amount of sugar than before. The alternative hypothesis will state that the mean grams of sugar in the bottle is different than 35. So, this is considered a two-tailed test. They're going to be in trouble if they put in significantly more than 35 grams or significantly less than 35 grams.

The distribution of a two-tailed test would look similar to the following curve:

Two-tailed test

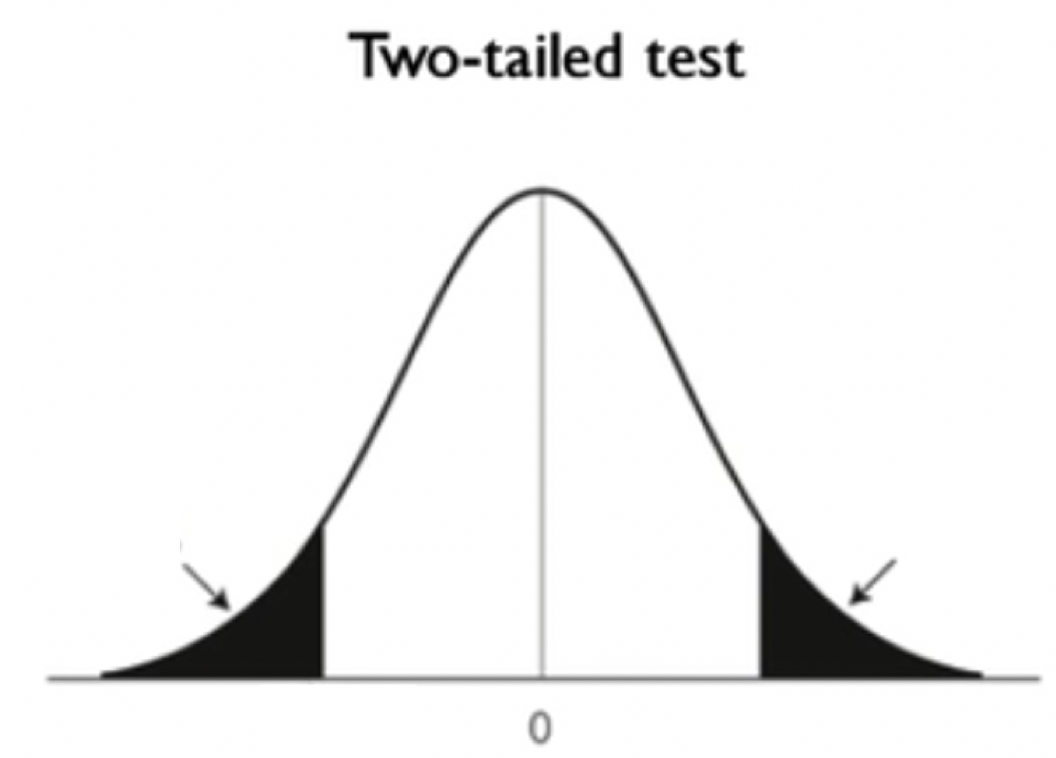
We are looking at the values that are extremely lower or higher than the assumed value.

term to know
Two-Tailed Test
A test for when you have reason to believe the population parameter is different from the assumed parameter value of the null hypothesis.

3. One-Tailed vs. Two-Tailed Tests

One-tailed tests are preferred to two-tailed tests because they're more powerful. Statistical power means that they have a higher likelihood of actually detecting a difference if one is present.

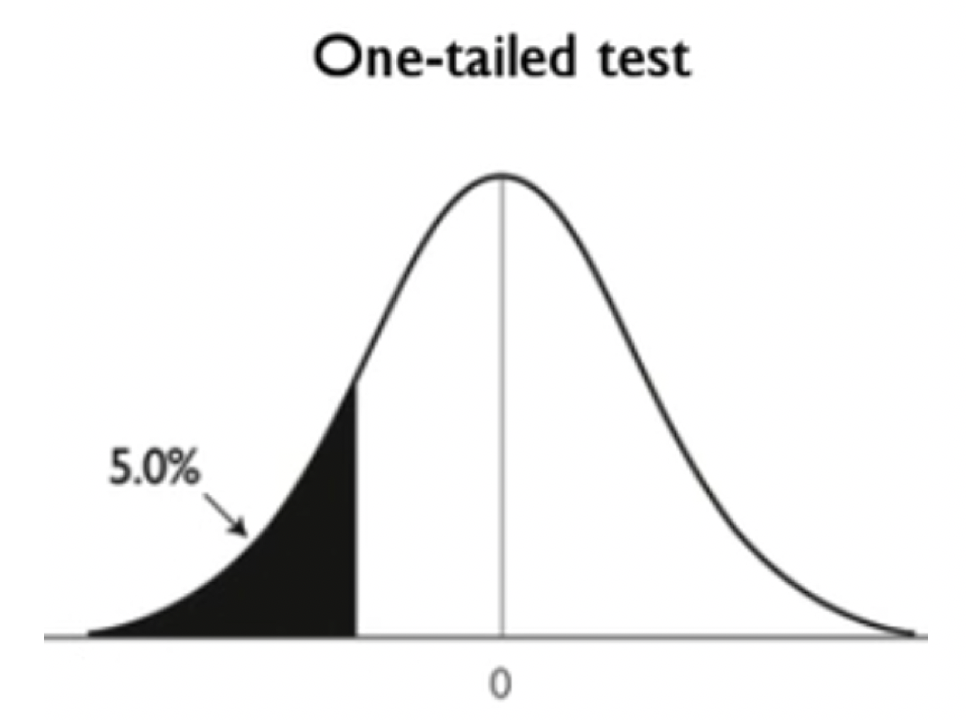
Let's take a look visually at what a one-tailed test and a two-tailed test look like. This is what a one-tailed test with a p-value of 5% would look like.

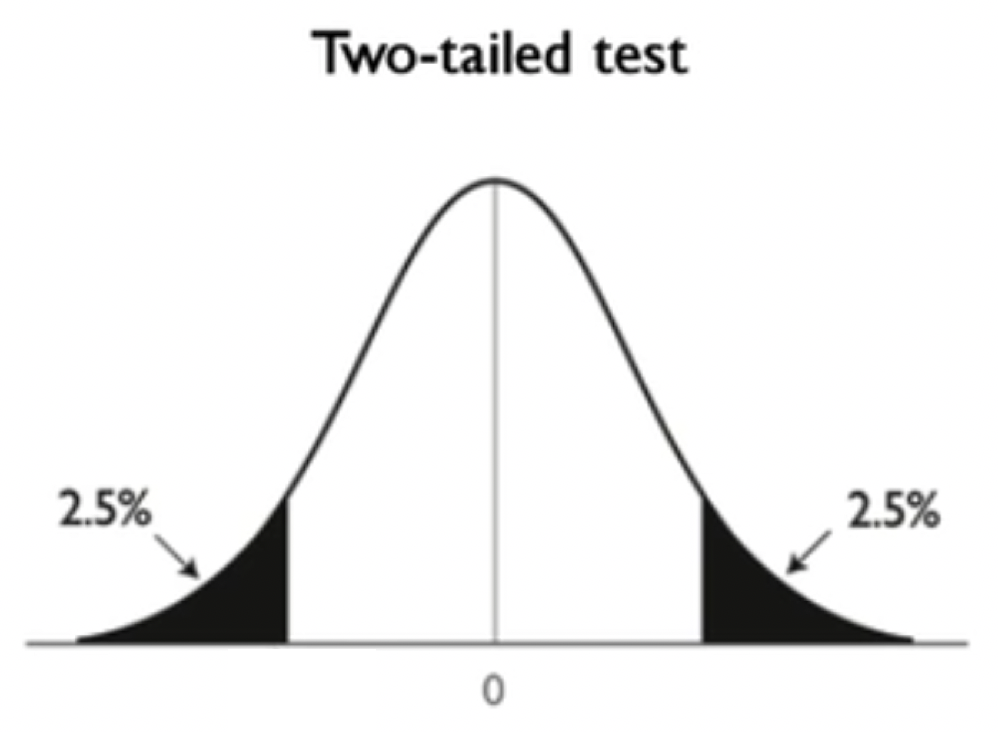
Comparing a One-Tailed Test and a Two-Tailed Test,
Both With a P-Value of 5%
One-tailed test with a p-value of 5% Two-tailed test with a p-value of 5%

With the one-tailed test, this would be under the alternative hypothesis that you have something less than a particular number, like a mean is less than 1, for example. You end up with one tail area here of about 5%. You're only going to get them in trouble if it's extremely lower than what you would have expected.

With the two-tailed test, you are interested in what the probability is that you would get at least as extreme on either side of a value as you ended up with from your sample. It could either be extremely low or extremely high—something that is extremely different from what you would have expected.

summary
One-tailed tests only test whether or not there is evidence of a statistic being significantly higher or lower than a claimed parameter, like mu or p. Two-tailed tests will test whether or not the statistic obtained, x-bar or p-hat, is significantly different from the claimed parameter. You learned about one-tailed tests, which have two versions, a left-tailed test, where you say in the alternative hypothesis that it's less than a claimed parameter, and a right-tailed test, which means that it's larger than the claimed parameter. There can also be a two-tailed test, where we simply claim that the true value is different than the claimed parameter, not equal to. When comparing one-tailed tests vs. two-tailed tests, one-tailed tests are preferred because they're more statistically powerful.

Good luck!

Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Terms to Know
Left-Tailed Test

A hypothesis test where the alternative hypothesis only states that the parameter is lower than the stated value from the null hypothesis.

One-Tailed Test

A test for when you have reason to believe the population parameter is higher or lower than the assumed parameter value of the null hypothesis

Right-Tailed Test

A hypothesis test where the alternative hypothesis only states that the parameter is higher than the stated value from the null hypothesis.

Two-Tailed Test

A test for when you have reason to believe the population parameter is different from the assumed parameter value of the null hypothesis.

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.