Table of Contents |
In various business data analytics applications, determining whether a single group’s mean differs from a known value is often necessary. For instance, a company might want to check if its average salary differs from the industry average. This can be assessed using a one-sample hypothesis test for the mean.
A one-sample hypothesis test for the mean is a statistical method used to compare the mean of a single sample to a known population mean. This test helps determine if the observed sample mean is significantly different from the hypothesized population mean, or if the difference could be due to random variation.
Recall in the last tutorial, steps were provided to perform a hypothesis test.
There are three types of hypothesis tests for a mean. Each one is discussed in the upcoming sections.
Let us walk through a practical example of performing a two-tailed hypothesis test for a mean.
EXAMPLE
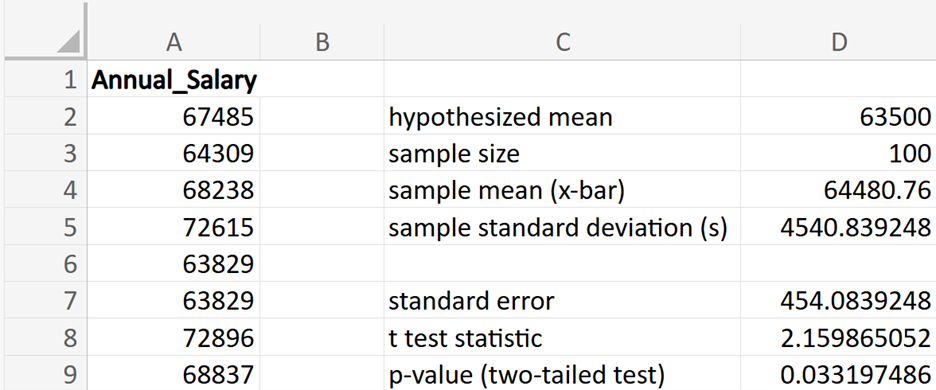
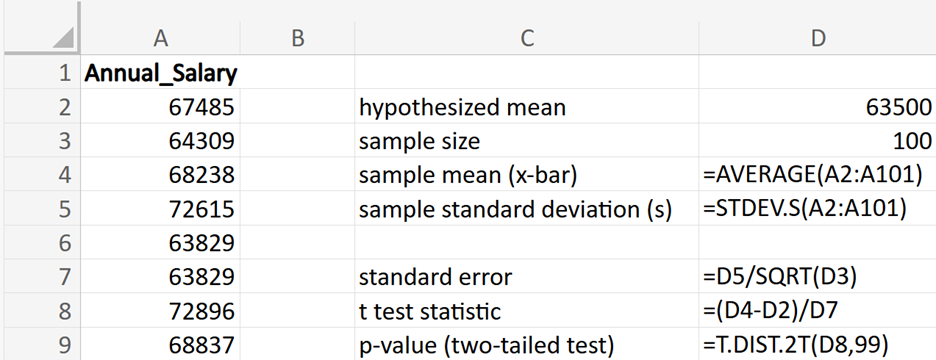
Tech Innovators Inc. is a rapidly growing technology company known for its innovative products and dynamic work environment. The company prides itself on offering competitive salaries to attract top talent. Recently, the HR department has raised concerns that the average annual salary of employees might have deviated from the industry average of $63,000. To address this concern, the company has decided to conduct a hypothesis test to determine if there has been a significant change in the average annual salary of its employees.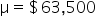
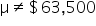
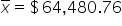 (sample mean; average value of the employee salaries in the sample)
(sample mean; average value of the employee salaries in the sample)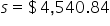 (sample standard deviation; amount of variability in the sample of employee salaries)
(sample standard deviation; amount of variability in the sample of employee salaries)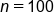 (sample size; number of observations in the sample)
(sample size; number of observations in the sample)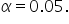
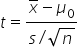 where μ₀ is the hypothesized mean in the null hypothesis, $63,500 in this example. This test statistic tells you how many standard deviations the sample mean is from the hypothesized mean of $63,500.
where μ₀ is the hypothesized mean in the null hypothesis, $63,500 in this example. This test statistic tells you how many standard deviations the sample mean is from the hypothesized mean of $63,500.
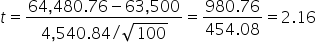
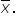 The green histogram below represents the distribution of sample means if you repeatedly sampled from the population with a mean of
The green histogram below represents the distribution of sample means if you repeatedly sampled from the population with a mean of 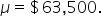 The sampling distribution of
The sampling distribution of 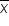 is centered around the hypothesized mean of
is centered around the hypothesized mean of  and has a standard deviation (standard error) of
and has a standard deviation (standard error) of 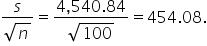
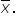 The area to the right of the blue dashed line represents the p-value, which is the probability of obtaining a test statistic as extreme as, or more extreme than, the observed test statistic (2.16) if the null hypothesis were true.
The area to the right of the blue dashed line represents the p-value, which is the probability of obtaining a test statistic as extreme as, or more extreme than, the observed test statistic (2.16) if the null hypothesis were true.
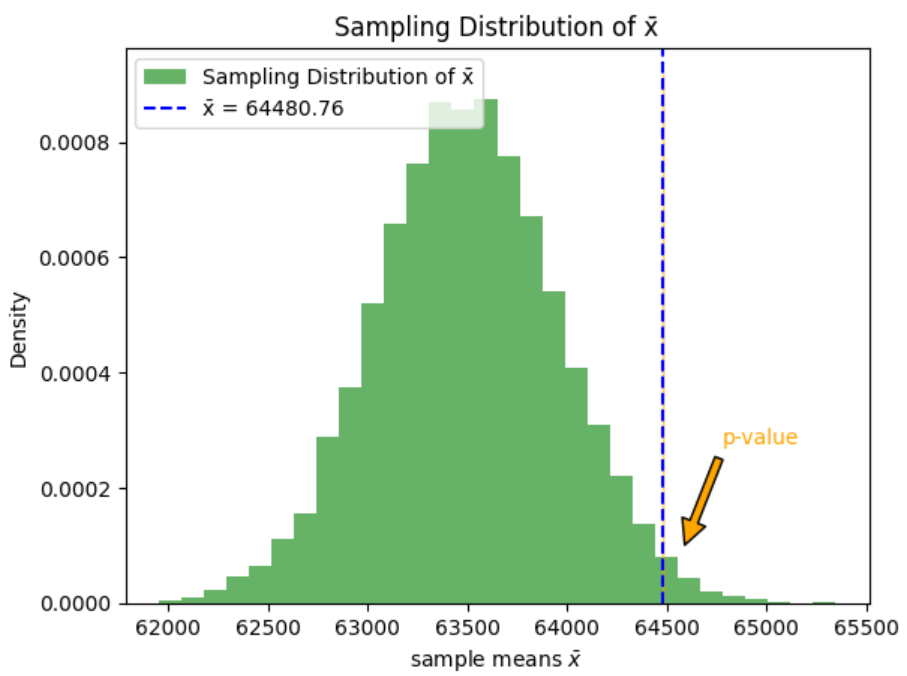
 to account for the sample size and variability. The test statistic (t) is a point on the t-distribution, indicating how many standard deviations
to account for the sample size and variability. The test statistic (t) is a point on the t-distribution, indicating how many standard deviations  is from the hypothesized mean,
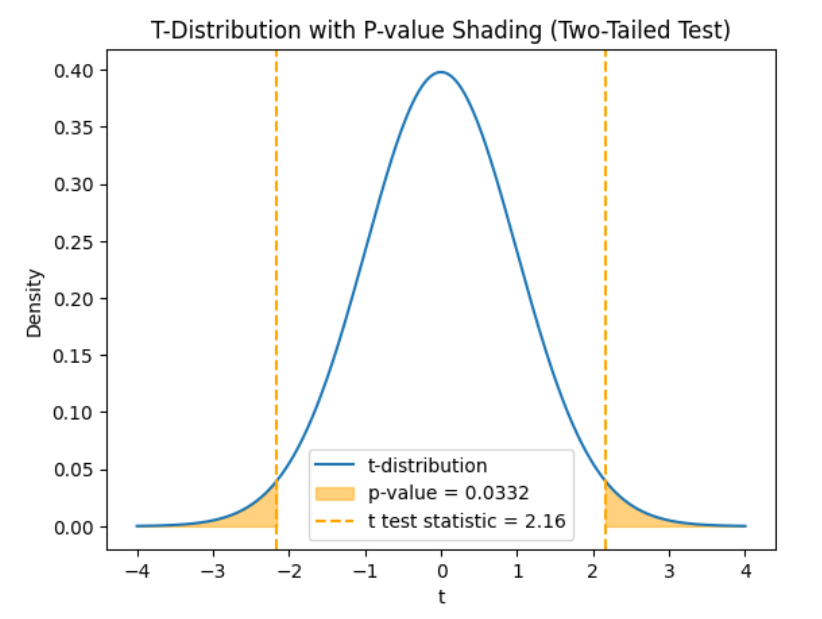
is from the hypothesized mean, 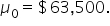 You use the t-distribution to find the p-value for the hypothesis test. The graph below shows the t-distribution for a two-tailed hypothesis test. The orange dashed lines at
You use the t-distribution to find the p-value for the hypothesis test. The graph below shows the t-distribution for a two-tailed hypothesis test. The orange dashed lines at  and
and 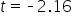 show the observed test statistics. The orange shaded areas represent the p-value, indicating the probability of observing test statistics as extreme as
show the observed test statistics. The orange shaded areas represent the p-value, indicating the probability of observing test statistics as extreme as 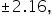 or more extreme, under the null hypothesis.
or more extreme, under the null hypothesis.
 for the high end.
for the high end. 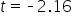 for the low end.
for the low end. 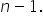
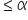 (level of significance), you can reject the null hypothesis.
(level of significance), you can reject the null hypothesis.
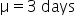
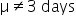
This table provides a guide on which Excel T.DIST() function to use for calculating p-values in different types of t-tests. It includes functions for two-tailed, right-tailed, and left-tailed tests, specifying the appropriate function and a brief description of each. The value of t in the table represents the test statistic.
| Type of Test | Excel Function | Description |
|---|---|---|
| Two-tailed | T.DIST.2T(t, df) | Calculates the two-tailed p-value for the t-distribution when the t test statistic is positive |
| T.DIST.2T(ABS(t), df) | P-value calculation when test statistic is negative | |
| Right-tailed | T.DIST.RT(t, df) | Calculates the right-tailed p-value for the t-distribution |
| Left-tailed | T.DIST(t, df, TRUE) | Calculates the left-tailed p-value for the t-distribution |
Let’s walk through a practical example of a right-tailed hypothesis test for a mean.
EXAMPLE
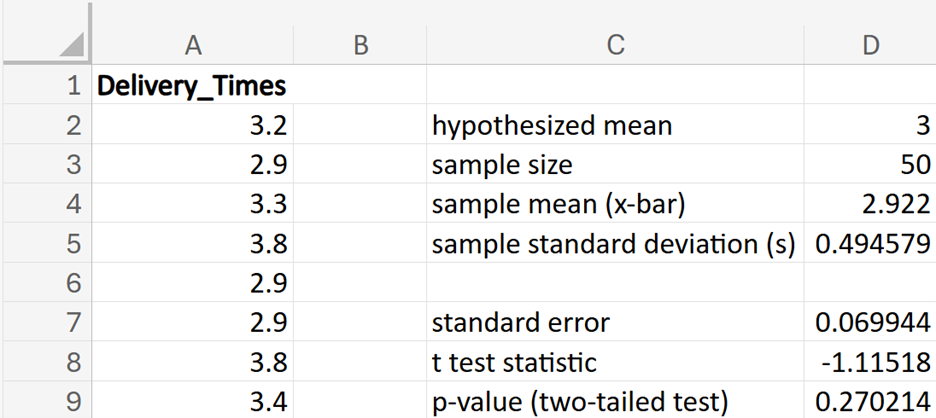
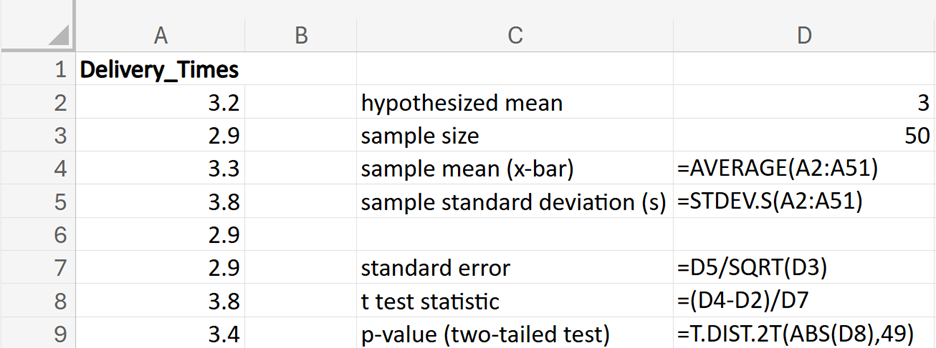
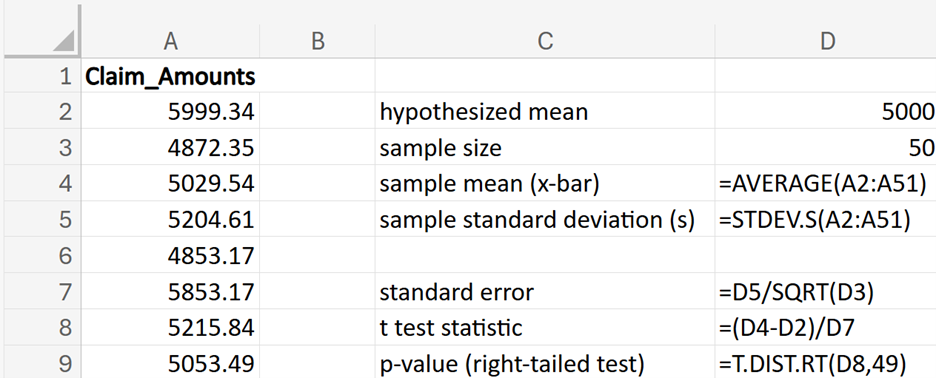
Financial Solutions Inc. is a well-established financial services company that prides itself on efficient operations and strong financial health. One key performance metric the company monitors closely is the average number of days it takes to collect accounts receivable. Historically, the company has maintained an average collection period of 30 days. Recently, there have been concerns that this period might have increased, potentially impacting cash flow and operational efficiency.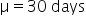
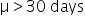
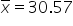
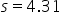
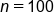
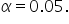
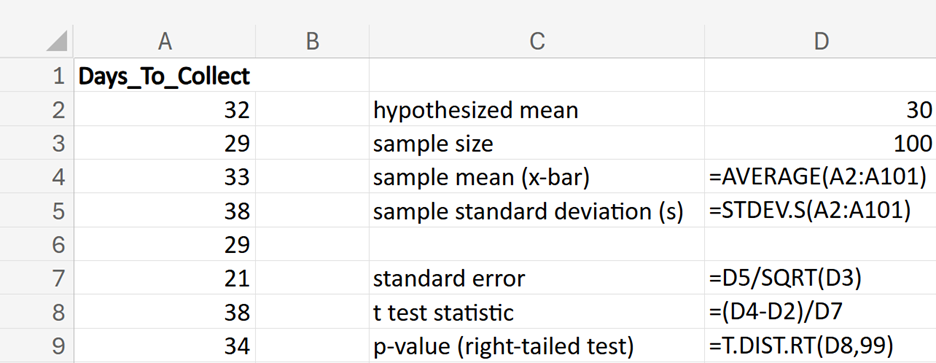
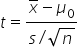 where μ₀ is the hypothesized mean in the null hypothesis, 30 days in this example.
where μ₀ is the hypothesized mean in the null hypothesis, 30 days in this example.
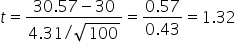
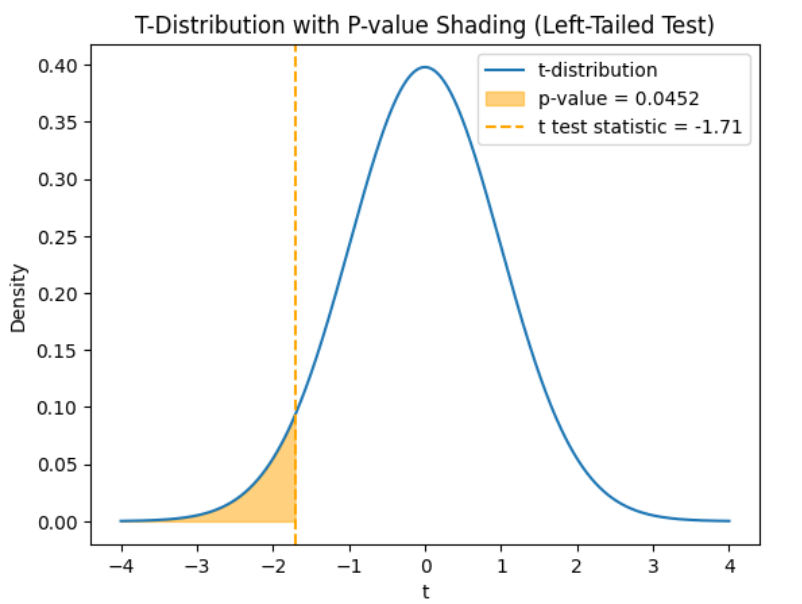
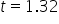 shows the observed test statistic. The orange shaded area represents the p-value, indicating the probability of observing the test statistic, or something more extreme, if the null hypothesis is true.
shows the observed test statistic. The orange shaded area represents the p-value, indicating the probability of observing the test statistic, or something more extreme, if the null hypothesis is true.
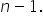
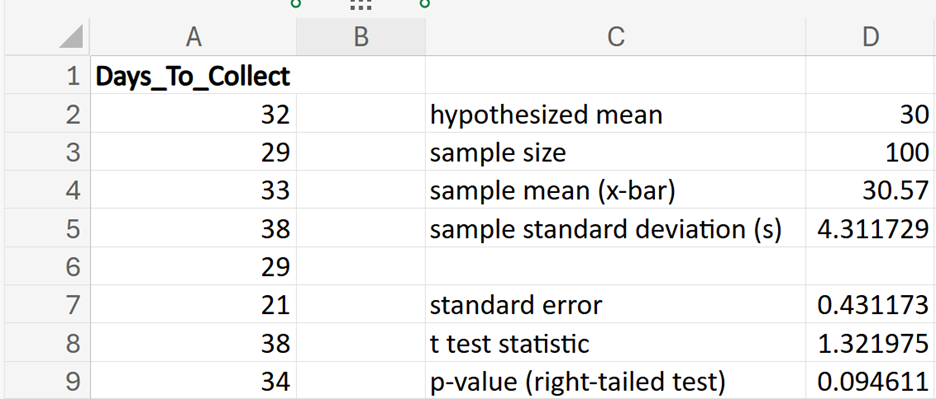
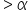 (level of significance), you fail to reject the null hypothesis.
(level of significance), you fail to reject the null hypothesis.
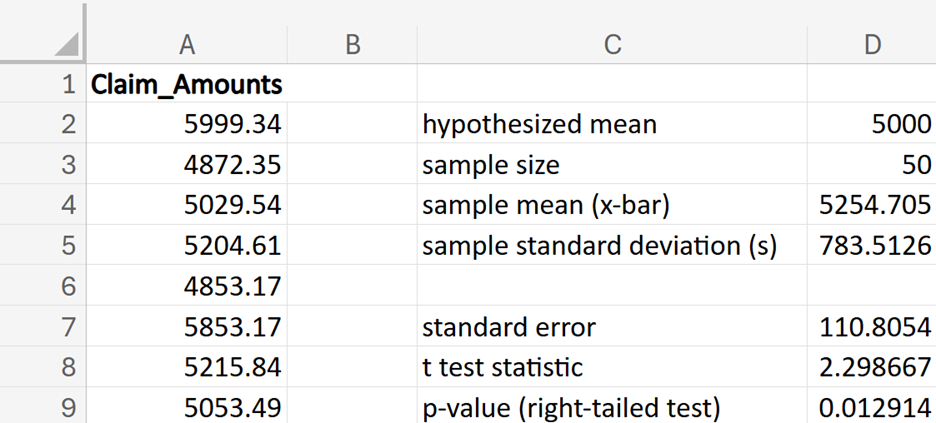
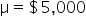
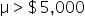
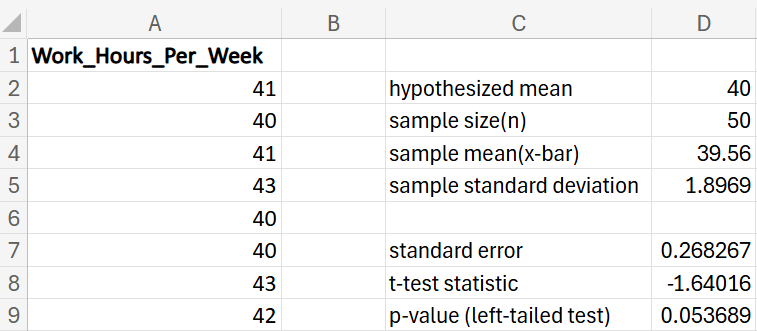
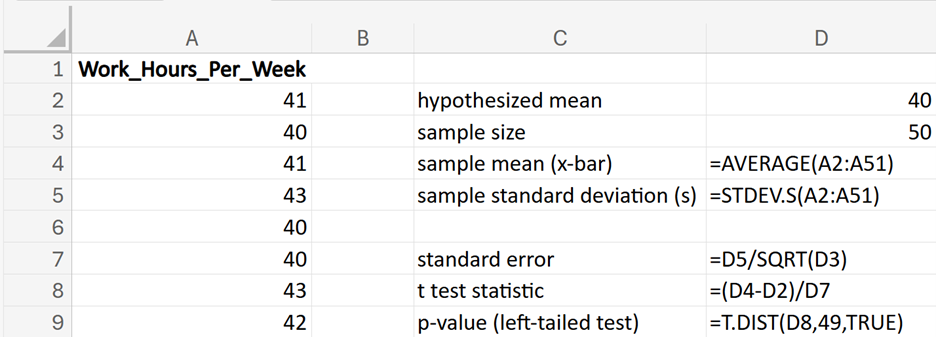
Let’s walk through a practical example of a left-tailed hypothesis test for a mean.
EXAMPLE
GreenTech Solutions, a leading company in sustainable technology, recently implemented a new expense tracking system aimed at reducing operating costs. The CFO (Chief Financial Officer) is keen to evaluate whether this new system has effectively decreased the average monthly operating costs, which were previously $200,000. To assess the impact, the CFO has decided to conduct a hypothesis test.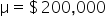
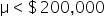
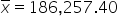
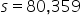
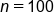
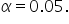
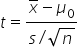 where μ₀ is the hypothesized mean in the null hypothesis, $200,000 in this example.
where μ₀ is the hypothesized mean in the null hypothesis, $200,000 in this example.
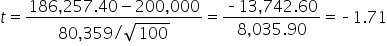
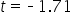 shows the observed test statistic. The orange shaded area represents the p-value, indicating the probability of observing the test statistic or something more extreme if the null hypothesis is true.
shows the observed test statistic. The orange shaded area represents the p-value, indicating the probability of observing the test statistic or something more extreme if the null hypothesis is true.
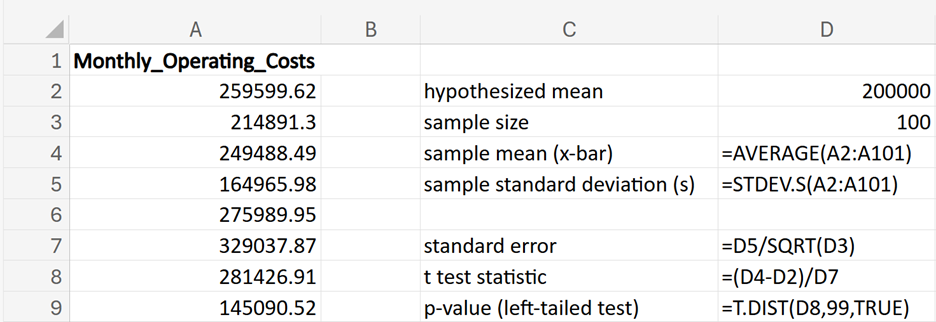
 The third argument is a logical value that specifies to calculate the cumulative probability up to the test statistic, which is the left-tailed p-value for the t-distribution.
The third argument is a logical value that specifies to calculate the cumulative probability up to the test statistic, which is the left-tailed p-value for the t-distribution.
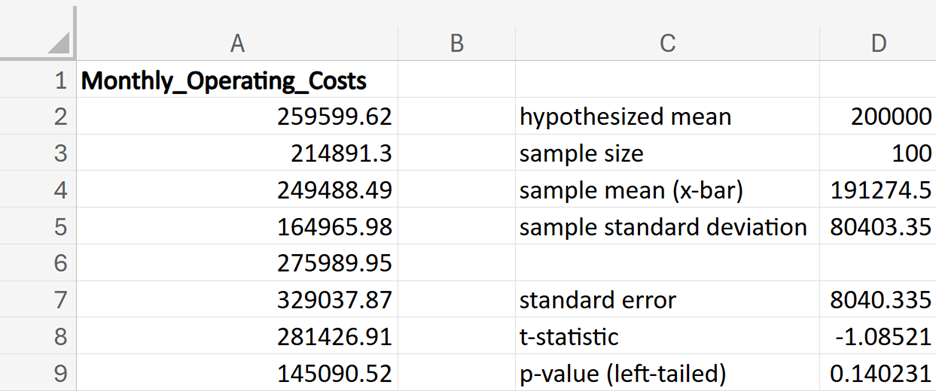
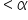 (level of significance), you reject the null hypothesis.
(level of significance), you reject the null hypothesis.
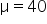
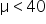
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.