Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Negative Exponents

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to simplify an expression with negative exponents. Specifically, this lesson will cover:

Table of Contents

1. Zero Exponents

Previously, we discussed that any number raised to a 0 exponent is equal to 1. Now that we have established some properties of exponents, we can see why.

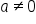To show this, let’s start with the expression a cubed over a cubed. Naturally, we need to assume that a not equal to 0 so that the denominator is not 0. Use the quotient property to simplify the expression.

a cubed over a cubed Use the quotient rule to subtract the exponents.
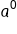
a to the power of 0 Our solution

Now, consider the same problem in a second way. We know that any quantity, divided by itself, is 1.

Therefore, 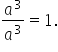a cubed over a cubed equals 1.

When we combine these two results, we get 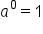a to the power of 0 equals 1, as long as 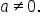a not equal to 0. This result is an important property that we’ll call the zero property of exponents:

formula to know
Zero Property of Exponents
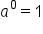
a to the power of 0 equals 1

Any number or expression raised to a zero power will always be 1.

EXAMPLE

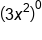
open parentheses 3 x squared close parentheses to the power of 0 Apply the zero power rule.
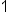
1 Our solution

2. Negative Exponents

2a. Rule #1

Another property we will consider here deals with negative exponents. Again, we will solve the following example in two ways.

EXAMPLE

Use the quotient property and solve.

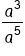
a cubed over a to the power of 5 Using the quotient rule, subtract the exponents.
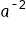
a to the power of short dash 2 end exponent Our solution

But now we consider the same problem in a second way:

EXAMPLE

Rewrite the exponents as repeated multiplication and solve.

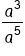
a cubed over a to the power of 5 Rewrite the exponents as repeated multiplication.
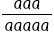
fraction numerator a a a over denominator a a a a a end fraction Reduce three 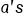a apostrophe s out of the top and bottom.
fraction numerator 1 over denominator a a end fraction Simplify to exponents.
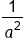
1 over a squared Our solution

When we combine these two results, we get 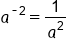a to the power of short dash 2 end exponent equals 1 over a squared. This example illustrates an important property of exponents. Negative exponents yield the reciprocal of the base. Once we take the reciprocal, the exponent is now positive. Also, it is important to note a negative exponent does not mean the expression is negative, only that we need the reciprocal of the base. This gives us Rule #1 of the properties of negative exponents.

formula to know
Properties of Negative Exponents
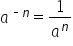
Rule #1: a to the power of short dash n end exponent equals 1 over a to the power of n

2b. Rule #2

Negative exponents can be combined in several different ways. Generally, if we think of our expression as a fraction, negative exponents in the numerator must be moved to the denominator; likewise, negative exponents in the denominator need to be moved to the numerator. When the base with the exponent moves, the exponent is now positive.

To see this, consider the expression 1 over x to the power of short dash 4 end exponent.

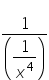
fraction numerator 1 over denominator open parentheses begin display style 1 over x to the power of 4 end style close parentheses end fraction Rewrite the denominator using the property of negative exponents.
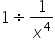
1 divided by 1 over x to the power of 4 Rewrite as a division problem.
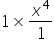
1 cross times x to the power of 4 over 1 Rewrite the fraction division as multiplication.
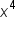
x to the power of 4 Simplify.

Thus, 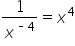1 over x to the power of short dash 4 end exponent equals x to the power of 4.

This gives us Rule #2 of the properties of negative exponents.

formula to know
Properties of Negative Exponents
Rule #2: 1 over a to the power of short dash n end exponent equals a to the power of n

watch

2c. Rule #3

What if you have an expression where a negative exponent is applied to the whole fraction?

Consider the expression 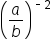open parentheses a over b close parentheses to the power of short dash 2 end exponent.

By using exponent properties learned previously, we can write this as an equivalent expression that contains only nonnegative exponents.

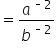
equals a to the power of short dash 2 end exponent over b to the power of short dash 2 end exponent Use the “fraction to a power rule” as presented previously.
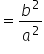
equals b squared over a squared Use the “rule #2” property.
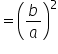
equals open parentheses b over a close parentheses squared This is equivalent to the previous answer.

The result is simply the reciprocal of the fraction, where each term in the numerator and denominator is raised to a positive power n. This gives us Rule #3 of the properties of negative exponents.

formula to know
Properties of Negative Exponents
Rule #3: open parentheses a over b close parentheses to the power of short dash n end exponent equals open parentheses b over a close parentheses to the power of n

big idea
Negative exponents yield the reciprocal of the base.

term to know
Reciprocal (of a number a)
The multiplicative inverse of a. In other words, the number 1 over a.

3. Simplifying With Negative Exponents

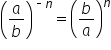
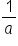Simplifying with negative exponents is much the same as simplifying with positive exponents. It is advised to keep the negative exponents until the end of the problem and then move them around to their correct location (numerator or denominator). As we do this, it is important to be very careful of rules for adding, subtracting, and multiplying with negatives.

EXAMPLE

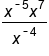
fraction numerator x to the power of short dash 5 end exponent x to the power of 7 over denominator x to the power of short dash 4 end exponent end fraction Simplify the numerator with the product rule, adding the exponents.
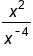
x squared over x to the power of short dash 4 end exponent Use the quotient rule to subtract exponents. Be careful with the negatives!
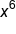
x to the power of 6 Our solution

EXAMPLE

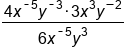
fraction numerator 4 x to the power of short dash 5 end exponent y to the power of short dash 3 end exponent times 3 x cubed y to the power of negative 2 end exponent over denominator 6 x to the power of short dash 5 end exponent y cubed end fraction Simplify the numerator with the product rule, adding the exponents.
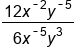
fraction numerator 12 x to the power of short dash 2 end exponent y to the power of short dash 5 end exponent over denominator 6 x to the power of short dash 5 end exponent y cubed end fraction Apply the quotient rule to subtract the exponents. Be careful with negatives!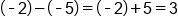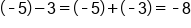
open parentheses short dash 2 close parentheses minus open parentheses short dash 5 close parentheses equals open parentheses short dash 2 close parentheses plus 5 equals 3
open parentheses short dash 5 close parentheses minus 3 equals open parentheses short dash 5 close parentheses plus open parentheses short dash 3 close parentheses equals short dash 8
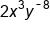
2 x cubed y to the power of short dash 8 end exponent The negative exponent needs to move down to the denominator.
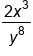
fraction numerator 2 x cubed over denominator y to the power of 8 end fraction Our solution

EXAMPLE

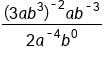
fraction numerator open parentheses 3 a b cubed close parentheses to the power of short dash 2 end exponent a b to the power of short dash 3 end exponent over denominator 2 a to the power of short dash 4 end exponent b to the power of 0 end fraction In the numerator, use the power rule with ‐2, multiplying the exponents. In the denominator, 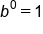b to the power of 0 equals 1.
fraction numerator 3 to the power of short dash 2 end exponent a to the power of short dash 2 end exponent b to the power of short dash 6 end exponent a b to the power of short dash 3 end exponent over denominator 2 a to the power of short dash 4 end exponent end fraction In the numerator, use the product rule to add the exponents.
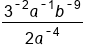
fraction numerator 3 to the power of short dash 2 end exponent a to the power of short dash 1 end exponent b to the power of short dash 9 end exponent over denominator 2 a to the power of short dash 4 end exponent end fraction Use the quotient rule to subtract the exponents. Be careful with negatives!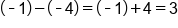
open parentheses short dash 1 close parentheses minus open parentheses short dash 4 close parentheses equals open parentheses short dash 1 close parentheses plus 4 equals 3
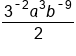
fraction numerator 3 to the power of short dash 2 end exponent a cubed b to the power of short dash 9 end exponent over denominator 2 end fraction Move 3 and b to the denominator because of negative exponents.
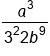
fraction numerator a cubed over denominator 3 squared 2 b to the power of 9 end fraction Evaluate 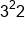3 squared 2.
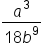
fraction numerator a cubed over denominator 18 b to the power of 9 end fraction Our solution

hint
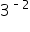In the previous example, it is important to point out that when we simplified 3 to the power of short dash 2 end exponent, we moved the 3 to the denominator, and the exponent became positive. We did not make the number negative! Negative exponents never make the bases negative; they simply mean we must take the reciprocal of the base.

summary
Any number or expression raised to a zero exponent will always be 1, known as the zero property of exponents. You can rewrite any negative exponent as positive using one of these properties. Any base, b, to a negative exponent, -n, can be written as 1 over the same base, b, to a positive exponent, n (rule #1). The exponent goes from negative to positive. We now have our base and exponent in the denominator of the fraction. It's like we have flipped the fraction.

Similarly, if you have a fraction, 1 over base, b, to a negative exponent, -n, we can write it as the same base b to the positive exponent n (rule #2). Again, our exponent goes from negative to positive. Instead of the base and exponent being in the denominator of the fraction, we have it written by itself.

When you have an expression where a negative exponent is applied to the whole fraction, we can apply rule #3 of the properties of negative exponents: By using exponent properties learned previously, we can write it as an equivalent expression that contains only nonnegative exponents.

Lastly, simplifying with negative exponents is much the same as simplifying with positive exponents. Keep the negative exponents until the end of the problem and then move them around to their correct location (numerator or denominator), being careful of rules for adding, subtracting, and multiplying with negatives.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Properties of Negative Exponents

Rule space # 1 colon thin space a to the power of negative n end exponent equals 1 over a to the power of n

Rule space # 2 colon space 1 over a to the power of negative n end exponent equals a to the power of n

Rule space # 3 colon space open parentheses a over b close parentheses to the power of negative n end exponent equals b to the power of n over a to the power of n

Zero Property of Exponents

a to the power of 0 equals 1

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.