Table of Contents |
Unlike adding and subtracting fractions, when multiplying or dividing fractions, you do not need a common denominator. Hooray! But why would you want to multiply a fraction? Remember, multiplication is just repeated addition. For example, if you want to make 4 times as many cookies for a bake sale, you don’t want to add the ingredients four times—just multiply and get your answer a lot faster. Additionally, multiplication and division involving fractions is useful when converting between measurements, which is common in many scientific fields, such as chemistry, physics, and nursing.
So how do you multiply fractions if you don’t need a common denominator? When you multiply fractions, you multiply the numerators together to find the numerator of your answer. Similarly, you multiply the denominators together to find the denominator of your answer. In other words, just multiply straight across!
EXAMPLE
Suppose you want to multiply 3/4 times 1/5.
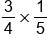
|
The expression |
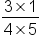
|
Multiply the numerators, 3 and 1, to find the final numerator. Multiply the denominators, 4 and 5, to find the final denominator. |
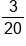
|
The final numerator is 3 and the final denominator is 20. The solution is 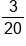 . .
|
EXAMPLE
You are cooking a recipe that calls for ¾ cups of water. You want to triple the recipe for a party you plan to go to. How much water will you need to triple the recipe?
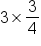
|
We need 3 times ¾ cups of water. |
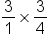
|
We can write the whole number 3 as a fraction by making the denominator 1. |
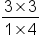
|
Now that we have 2 fractions, we can multiply across. |
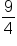
|
The numerator is larger than the denominator so this is an improper fraction. We must simplify the fraction to determine the amount of water needed. |
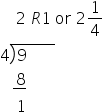
|
When we divide 9 by 4, we get 2 with a remainder of 1. |
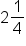
|
We will need to add 2 ¼ cups of water to triple the recipe. |
So far, we’ve only converted whole numbers into improper fractions so we can multiply them, but what if we had a mixed fraction like 1 ½? Let’s think about it like a pizza again.

Here, we have 1 ½ pizzas….or 3/2. But how do we do this mathematically so we don’t have to draw pizzas each time? You multiply the denominator with the whole number and then add the numerator.

So, if we multiply the denominator (2) with the whole number (1), we get 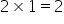 . Then, add the numerator (1), or
. Then, add the numerator (1), or 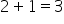 . So, 1 ½ can be written as 3/2.
. So, 1 ½ can be written as 3/2.
EXAMPLE
Convert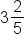 to an improper fraction
to an improper fraction

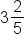
|
The fraction |
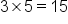
|
Multiply the denominator by the whole number. |
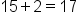
|
Add the numerator. |
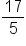
|
Put this value as the numerator, and keep the original denominator |
Now that we know how to multiply fractions, dividing fractions is similar. Technically, you can’t divide fractions. No, that doesn't mean this lesson is done. When dividing fractions, you’ll need to multiply by the reciprocal. Reciprocal means “opposite,” so finding the reciprocal of a fraction means flipping it, or switching the numerator and the denominator.
EXAMPLE
Suppose you want to divide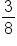 by
by 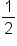 .
.
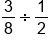
|
The expression |
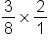
|
First, find the reciprocal of 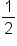 by flipping it. This is by flipping it. This is 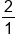 . Change the sign to multiplication. . Change the sign to multiplication.
|
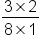
|
Next, multiply the numerators, 3 and 2, and multiply the denominators, 8 and 1. |
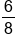
|
Since the numerator is 6 and the denominator is 8, the answer is 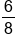 . .
|
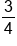
|
Now simplify the fraction. Our common factor is 2 so divide your numerator and denominator by 2. |
EXAMPLE
Divide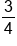 by
by 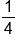 .
.
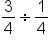
|
The expression |
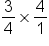
|
First, find the reciprocal of 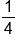 by flipping it. This is by flipping it. This is 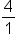 . Change the sign to multiplication. . Change the sign to multiplication.
|

|
Next, multiply the numerators, 3 and 4, and multiply the denominators, 4 and 1. |
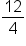
|
Our solution 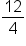 is an improper fraction. We can convert this to a mixed fraction by dividing 12 by 4. is an improper fraction. We can convert this to a mixed fraction by dividing 12 by 4.
|

|
This divides evenly 3 times, so our solution is 3 by converting our improper fraction 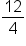 into a whole number. into a whole number.
|
EXAMPLE
You have a 5-pound bag of sand. You want to pour 1 1/4 pounds of sand each into jars for table centerpieces. How many centerpieces can you make with the 5 pounds of sand?
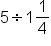
|
We want to divide 5 pounds by 1 ¼. |
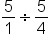
|
We can write the whole number as a fraction by writing it over 1. We will also need to convert the mixed fraction 1 ¼ into an improper fraction. We multiply the whole number (1) by the denominator (4), 1x4 = 4, then we add this to the numerator of the mixed fraction 1 (4 + 1 = 5). 1 ¼ written as an improper fraction is 5/4. |
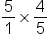
|
Next, find the reciprocal of 5/4 by flipping it. This is 4/5. Change the sign to multiplication. |
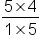
|
Multiply the numerators, 5 and 4, and the denominators, 1 and 5. |
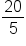
|
We get the fraction 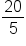 This is an improper fraction and we can simplify this by converting it to a mixed number. This is an improper fraction and we can simplify this by converting it to a mixed number.
|
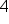
|
We divide 20 by 5 and get a solution of 4. So we can divide the 5-pound bag of sand into 4 jars. |
Problem Solving: Apply Your Skill |
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.