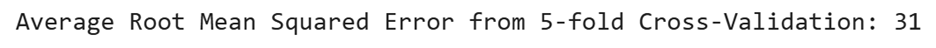EXAMPLE
You are a data analyst at TechPulse Dynamics. The tech company is planning to launch a new wearable fitness tracker. The company wants to predict the success of this product launch based on historical data from previous product launches. This will help the company make informed decisions about marketing strategies, production planning, and resource allocation.
The data is contained in an Excel file named product_launch.xlsx that is stored in a GitHub repository here:
https://raw.githubusercontent.com/sophiaAcademics/BDA_Excel/main/StudentData/Tutorials/Unit5/5.3.2/product_launch.xlsx
The data set description is provided below.
Features:
-
Price: The price of the product.
-
Marketing_Spend: The amount of money spent on marketing the product.
-
Social_Media_Mentions: The number of times the product was mentioned on social media.
-
Pre_Orders: The number of pre-orders received before the launch.
-
Customer_Reviews: The number of customer reviews received within the first month.
-
Average_Rating: The average customer rating for the product (1 to 5).
Target Variable:
-
Success_Score: A numerical score from 1 to 100 where higher numbers represent a more successful product launch (higher numbers correspond to higher revenue).
Additional Variable:
-
Product_ID: A unique identifier for each product.
Your goal is to create a multiple linear regression model that reliably generalizes new data. In other words, the model should not only fit the historical data well, but also provide accurate predictions for future product launches.
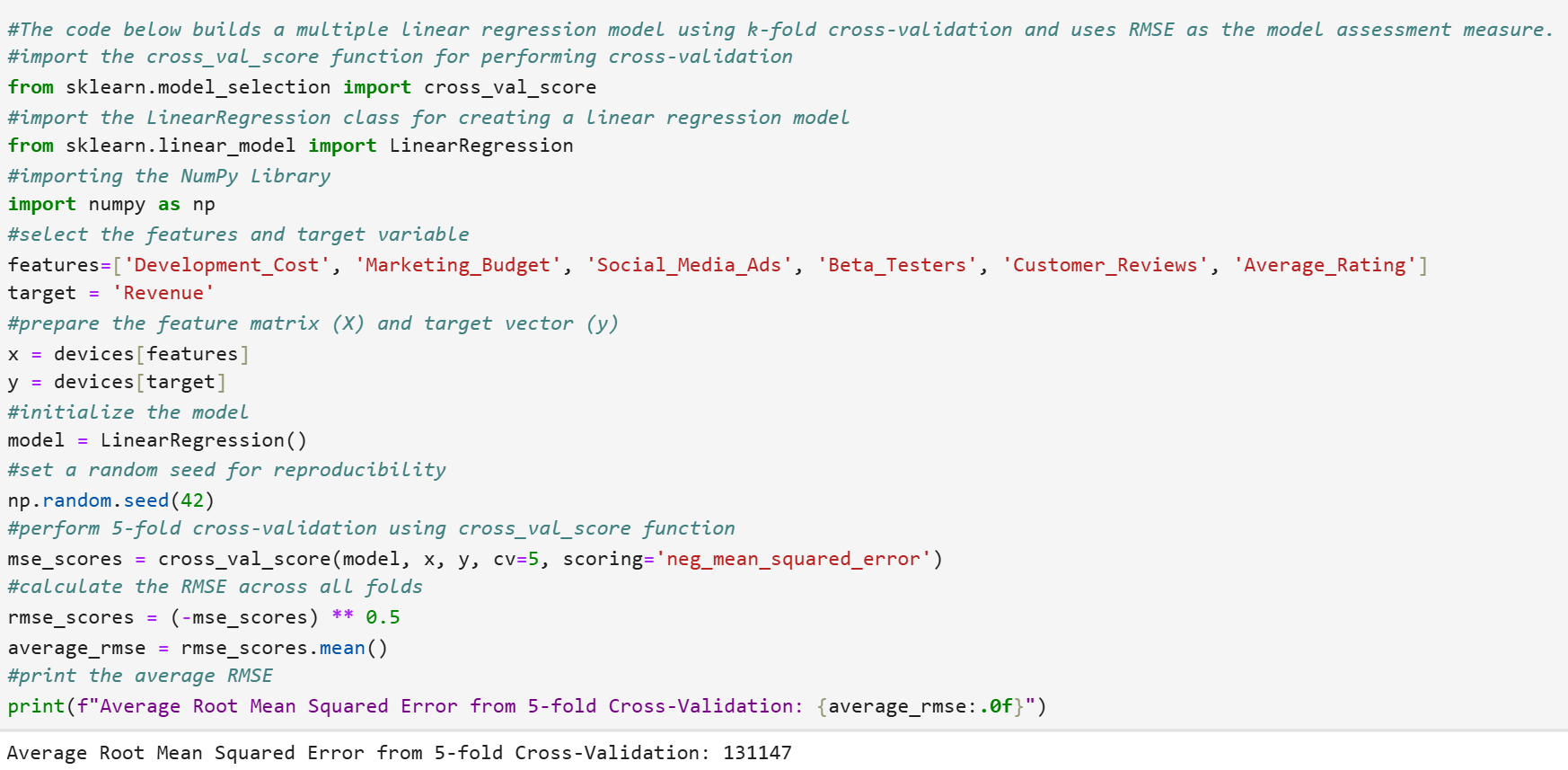
The code below imports pandas, imports an Excel file from a URL, and creates a pandas DataFrame named product_launch before creating a multiple regression model.
Let’s break down the steps of the code line by line.
Step 1: Import the necessary functions and classes.
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
import numpy as np
- These lines import the necessary functions and classes from the sklearn library:
- cross_val_score: This function is used to evaluate a model using cross-validation.
- LinearRegression: This class is used to create a linear regression model.
- The last line imports the Numpy library and gives it the nickname np for easier use in your code.
Step 2: Select the features and target variable.
features = ['Price', 'Marketing_Spend', 'Social_Media_Mentions', 'Pre_Orders', 'Customer_Reviews', 'Average_Rating']
target = 'Success_Score'
- These lines specify the columns from the dataset that will be used as features and the target variable:
- features: A list of column names that represent the features for the model. The column names are separated by commas and enclosed in single quotes.
- target: The column name that represents the target variable the model will predict.
Step 3: Prepare the feature matrix (x) and target vector (y).
x = product_launch[features]
y = product_launch[target]
- These lines create the feature matrix, x, and the target vector, y:
- x: A data frame containing the feature columns specified in the features list.
- y: A column containing the target variable specified by target.
Step 4: Initialize the model.
model = LinearRegression()
- This line initializes a linear regression model.
You may remember from a previous tutorial when you were building regression models that you used the statsmodels library to build a simple linear regression model. The code
sm.OLS(y, x).fit() created a regression model.
Why can you not use this same code when you are building a regression model in the context of machine learning?
The statsmodels library is useful for statistical analysis and gives detailed information about the model, like the significance of each variable. However, when you are building models for machine learning, you often need to handle larger datasets and focus on making accurate predictions. This is where the scikit-learn library comes in.
The LinearRegression() function from the scikit-learn library is designed specifically for machine learning tasks. It has tools to help with things like splitting data into training and testing sets and performing cross-validation. So, while statsmodels is useful for understanding the details of a model, scikit-learn is better suited for building and testing models in a machine learning context.
Step 5: Set a random seed.
np.random.seed(42)
- This line sets the random seed to 42, ensuring that the random processes involved in k-fold cross-validation, such as the random shuffling of data before splitting it into folds, produce the same results each time the code is run. This helps in obtaining consistent and reproducible RMSE values. The Numpy library has a built-in function, random_seed, that allows you to set a random seed using any numerical value.
Let’s explore a random seed in simple terms.
Imagine you have a deck of cards, and you want to shuffle them. Each time you shuffle, the order of the cards will be different. Now, let's say you want to make sure that every time you shuffle, you get the exact same order of cards. To do this, you can use a random seed.
A random seed is like a special code or number that you use before shuffling. When you use the same seed, it tells the shuffling process to arrange the cards in the same way every time. So, if you use the seed 42 today and shuffle the cards, and then use the seed 42 again tomorrow and shuffle, you will obtain the same order of cards both times.
In coding, you use a random seed to make sure that any random processes, like shuffling data or picking random numbers, give you the same results every time you run the code. This helps you check your work and make sure your results are consistent. The seed can be any numerical value between 0 and close to 5 billion!
Step 6: Perform 5-fold cross-validation using cross_val_score function.
mse_scores = cross_val_score(model, x, y, cv=5, scoring='neg_mean_squared_error')
- This line performs 5-fold cross-validation and calculates the mean squared error (MSE) for each fold:
- cross_val_score: A function from the sklearn.model_selection module that evaluates a model using cross-validation.
- model: The linear regression model to be evaluated.
- x: The feature matrix.
- y: The target vector.
- cv=5: Specifies 5-fold cross-validation.
- scoring='neg_mean_squared_error': Specifies that the negative mean squared error should be used as the scoring metric. The negative value is used because cross_val_score expects a metric where higher values are better, but for MSE, lower values are better.
- Normally, MSE is calculated as the average of the squared differences between the actual and predicted values. Lower MSE indicates better model performance.
- scikit-learn's cross_val_score function expects higher scores to indicate better performance. To fit this convention, it returns the negative of the MSE values when scoring='neg_mean_squared_error' is specified.
Step 7: Calculate the RMSE across all folds.
rmse_scores = (-mse_scores) ** 0.5
average_rmse = rmse_scores.mean()
- These lines calculate the RMSE for each fold, and then compute the average RMSE:
- rmse_scores: After obtaining the negative MSE values from cross_val_score, you take the square root of the negative values to get the RMSE. This conversion ensures that the RMSE values are positive and in the same units as the target variable.
- average_rmse: The mean of the RMSE values across all folds.
Step 8: Print the average RMSE.
print(f"Average Root Mean Squared Error from 5-fold Cross-Validation: {average_rmse:.0f}")
- This line prints the average RMSE from the 5 folds using format strings.
The average RMSE value for this model is 31 success score points, as shown in the output below. The RMSE value has been rounded to 0 decimal places.
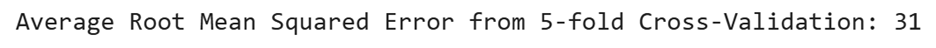 Interpretation of RMSE in Context
Interpretation of RMSE in Context
The RMSE value of 31 success score points indicates the average deviation of the predicted success scores from the actual success scores. This means that, on average, the model's predictions are off by 31 points.
Insights Based on the RMSE Value
1. Model Accuracy
-
Understanding Prediction Accuracy: An RMSE of 31 suggests that while the model provides a reasonable estimate, there is still a notable difference between the predicted and actual success scores. This level of accuracy might be acceptable depending on the company's tolerance for prediction discrepancies.
2. Decision Making
-
Risk Assessment and Critical Thresholds:
- A critical threshold is a specific value that helps decide if something is successful or not. Imagine you have a test score, and the passing mark is 70. If you score 69, you fail, but if you score 70 or above, you pass. Here, 70 is the critical threshold.
- For TechPulse Dynamics, let's say the company decides that a product needs a success score of at least 75 to be considered successful. This 75 is the critical threshold.
- The RMSE of 31 means that the model's predictions can be off by 31 points. So, if the model predicts a success score of 80 for a new product, the actual success score could be anywhere from 49 to 111 (80 ± 31).
-
Close to Threshold: If the predicted score is close to 75 (like 80), the company needs to be cautious. The actual score might be below 75, meaning the product might not be as successful as hoped.
-
Far from Threshold: If the predicted score is much higher (like 100), even with the RMSE, the product is likely to be successful.
3. Resource Allocation
-
Budgeting for Uncertainty: Given the RMSE, the company might allocate additional resources to account for potential inaccuracies in the predictions. For instance, if the model predicts high product success scores, the company could still prepare for a lower-than-expected outcome by setting aside contingency funds.
-
Production Flexibility: The RMSE can guide the company to maintain flexibility in production planning. With a 31-point difference between predicted and actual scores, the company might adopt a more conservative approach to avoid overproduction or underproduction.
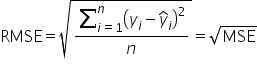
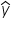 is the predicted target value (the value predicted by the predictive model)
is the predicted target value (the value predicted by the predictive model)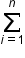 denotes the sum over all the observations 1 to n
denotes the sum over all the observations 1 to n