Models with Binary Variables

1. Introduction to Binary Integer Linear Programming

1a. Definition

Binary integer linear programming is a specialized type of integer programming where the decision variables can only be 0 or 1. This technique helps find the best solution to an optimization problem within a set of constraints, using binary variables to represent yes/no decisions. The method is particularly useful in business data analytics for making decisions like whether to open a new store (1) or not (0), whether to launch a marketing campaign (1) or not (0), or whether to assign a sales representative to a region (1) or not (0).

By using binary variables, you can meet more restrictive requirements for a business data analytics optimization problem by precisely modeling decisions that are either/or in nature. This allows you to enforce specific conditions, such as ensuring that only one project is selected from a group, or that a resource is either fully utilized or not used at all. This level of detail helps create more accurate and feasible solutions that align closely with business constraints and goals.

term to know

Binary Integer Linear Program

A type of optimization model where the objective function and constraints are linear, but the decision variables are restricted to binary values.

1b. Importance in Decision-Making for Business Data Analytics

There are several reasons why binary integer linear programming problems are important in business data analytics. Several of them are listed below.

Precision in Decision-Making:

• Binary variables allow for precise modeling of yes/no decisions, which are common in business scenarios. This precision helps ensure that the solutions are practical and aligned with business requirements.

• Businesses often need to allocate limited resources efficiently. By using binary variables, companies can determine the optimal allocation of resources.
• The binary nature of the decision variables allows for clear, yes/no decisions, such as whether to buy a new piece of equipment (1) or not (0) or whether to allocate funds to a department (1) or not (0). This binary approach simplifies complex decision-making processes, ensuring that resources are allocated in the most effective way to achieve business objectives.

• Businesses can use binary integer linear programming to assess and mitigate risks by modeling different risk scenarios and their impacts.
• For example, a company could use binary integer linear programming to decide whether to invest in a backup server (1) or not (0), ensuring business continuity and protection against data loss.

2. Applications of Binary Integer Linear Programming

In this section, you will explore the practical applications of binary integer linear programming by formulating the problem. By working through these examples, you will gain hands-on experience in using binary variables to formulate an optimization model in various business contexts.

2a. Production Planning Example

Let’s formulate a binary integer linear programming problem for a production planning application. This example will help you see how binary variables will help you make clear, yes/no decisions in optimizing a production process while adhering to resource constraints.

EXAMPLE

A company manufactures three products: A, B, and C. Each product requires a certain amount of raw materials and labor hours. The company has a limited supply of raw materials and labor hours available each month. The goal is to maximize the total profit while staying within the resource constraints. The details are as follows: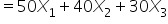

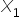• Product A:
  • Profit per unit: $50
  • Raw materials required per unit: 3 units
  • Labor hours required per unit: 2 hours
• Product B:
  • Profit per unit: $40
  • Raw materials required per unit: 2 units
  • Labor hours required per unit: 1 hour
• Product C:
  • Profit per unit: $30
  • Raw materials required per unit: 1 unit
  • Labor hours required per unit: 2 hours

The company has a total of 100 units of raw materials and 80 labor hours available each month. The company can choose to produce a product (1) or not (0).

For this scenario, specify the objective function, decision variables, and the constraints.

Objective Function: Maximize Profit

Decision Variables:

• : if the company produces product A; 0 otherwise
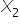• : 1 if the company produces product B: 0 otherwise
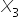• : 1 if the company produces product C; 0 otherwise

Constraints:

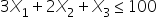1. (raw materials constraint)

This constraint ensures that the total amount of raw materials used for producing the products does not exceed the available supply of 100 units.

Specifically, producing one unit of Product A requires 3 units of raw materials, one unit of Product B requires 2 units, and one unit of Product C requires 1 unit. The sum of the raw materials used for all selected products must be within the limit.

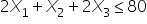2. (labor hours constraint)

This constraint ensures that the total labor hours required for producing the products do not exceed the available 80 labor hours.

Producing one unit of Product A requires 2 labor hours, one unit of Product B requires 1 labor hour, and one unit of Product C requires 2 labor hours. The total labor hours used for all selected products must be within the limit.

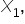
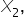3. and 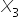in {0,1} (production decision)

This constraint specifies that each product can either be produced (1) or not produced (0).

The binary nature of these variables allows for clear, yes/no decisions regarding the production of each product, ensuring that the model accurately reflects the decision-making process.

Now, you see if you can formulate a binary linear integer programming problem using a similar production planning scenario!

try it

A bakery produces three types of baked goods: bread, cakes, and cookies. Each type of baked good requires a certain amount of flour and baking time. The bakery has a limited supply of flour and a limited number of baking hours available each day. The goal is to maximize the total profit while staying within the resource constraints. The details are as follows:

• Bread:
  • Profit per unit: $5
  • Flour required per unit: 4 pounds
  • Baking time required per unit: 3 hours
• Cakes:
  • Profit per unit: $10
  • Flour required per unit: 6 pounds
  • Baking time required per unit: 2 hours
• Cookies:
  • Profit per unit: $8
  • Flour required per unit: 2 pounds
  • Baking time required per unit: 1 hour

The bakery has a total of 110 pounds of flour and 30 baking hours available each day. The bakery can choose to produce a type of baked good (1) or not (0).

For this scenario, find the objective function, decision variables, and the constraints.

Solution:

Objective Function: Maximize Profit

Decision Variables:

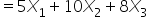
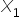• : 1 if the bakery produces bread; 0 otherwise
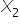• : 1 if the bakery produces cakes: 0 otherwise
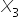• : 1 if the bakery produces cookies; 0 otherwise

Constraints:

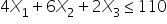1. (flour constraint)

This constraint ensures that the total amount of flour used for producing the baked goods does not exceed the available supply of 110 pounds.

Specifically, producing one unit of bread requires 4 pounds of flour, one unit of cake requires 6 pounds, and one unit of cookies requires 2 pounds. The sum of the flour used for all selected baked goods must be within the limit of 110 pounds.

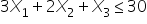2. (baking time constraint)

This constraint ensures that the total baking time required for producing the baked goods does not exceed the available 30 baking hours.

Producing one unit of bread requires 3 hours of baking time, one unit of cake requires 2 hours, and one unit of cookies requires 1 hour. The total baking time used for all selected baked goods must be within the limit of 30 hours.

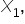
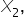3. and 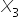in {0,1} (production decision)

This constraint specifies that each type of baked good can either be produced (1) or not produced (0).

The binary nature of these variables allows for clear, yes/no decisions regarding the production of each type of baked good, ensuring that the model accurately reflects the decision-making process.

2b. Event Planning Example

Let’s try formulating one more binary integer linear program to ensure you fully grasp how to apply a binary integer linear programming problem to different real-world scenarios.

EXAMPLE

A company is organizing a music festival and needs to decide which artists to book for the event. The goal is to maximize the total expected attendance while staying within a budget of $200,000. Each artist has a booking fee and an expected number of attendees they will attract. The company can choose to book an artist (1) or not (0). The details are as follows: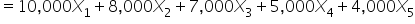

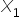• Artist A:
  • Booking Fee: $80,000
  • Expected Attendance: 10,000
• Artist B:
  • Booking Fee: $60,000
  • Expected Attendance: 8,000
• Artist C:
  • Booking Fee: $50,000
  • Expected Attendance: 7,000
• Artist D:
  • Booking Fee: $40,000
  • Expected Attendance: 5,000
• Artist E:
  • Booking Fee: $30,000
  • Expected Attendance: 4,000

For this scenario, specify the objective function, decision variables, and the constraints.

Objective Function: Maximize Total Attendance

Decision Variables:

• : 1 if the company books artist A; 0 otherwise
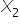• : 1 if the company books artist B; 0 otherwise
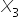• : 1 if the company books artist C; 0 otherwise
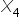• : 1 if the company books artist D; 0 otherwise
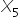• : 1 if the company books artist E; 0 otherwise

Constraints:

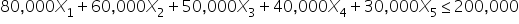1. (budget constraint)

This constraint ensures that the total booking fees for all the selected artists do not exceed the available budget of $200,000.

Specifically, booking Artist A costs $80,000, Artist B costs $60,000, Artist C costs $50,000, Artist D costs $40,000, and Artist E costs $30,000. The sum of the booking fees for all chosen artists must be within the budget limit.

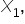
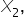
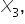
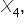2. and 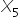in {0,1} (booking decision)

This constraint specifies that each artist can either be booked (1) or not booked (0).

The binary nature of these variables allows for clear, yes/no decisions regarding the booking of each artist, ensuring that the model accurately reflects the decision-making process

Now, you see if you can formulate a similar event planning using a binary integer linear programming problem.

try it

A company is organizing a tech conference and needs to decide which speakers to invite. The goal is to maximize the total expected attendance while staying within a budget of $150,000. Each speaker has a speaking fee and an expected number of attendees they will attract. Additionally, the company wants to ensure that at least one speaker specializes in artificial intelligence (AI). The company can choose to invite a speaker (1) or not (0). The details are as follows:

• Speaker A:
  • Speaking Fee: $50,000
  • Expected Attendance: 5,000
  • Specializes in AI: Yes
• Speaker B:
  • Speaking Fee: $40,000
  • Expected Attendance: 4,000
  • Specializes in AI: No
• Speaker C:
  • Speaking Fee: $30,000
  • Expected Attendance: 3,500
  • Specializes in AI: Yes
• Speaker D:
  • Speaking Fee: $20,000
  • Expected Attendance: 2,500
  • Specializes in AI: No
• Speaker E:
  • Speaking Fee: $10,000
  • Expected Attendance: 1,500
  • Specializes in AI: No

For this scenario, find the objective function, decision variables, and the constraints.

Solution:

Objective Function: Maximize Total Expected Attendance

Decision Variables:

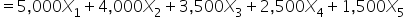
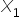• : 1 if the company invites speaker A; 0 otherwise
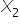• : 1 if the company invites speaker B; 0 otherwise
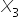• : 1 if the company invites speaker C; 0 otherwise
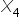• : 1 if the company invites speaker D; 0 otherwise
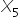• : 1 if the company invites speaker E; 0 otherwise

Constraints:

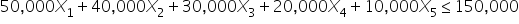1. (budget constraint)

This constraint ensures that the total speaking fees for all the selected speakers do not exceed the available budget of $150,000.

Specifically, inviting Speaker A costs $50,000, Speaker B costs $40,000, Speaker C costs $30,000, Speaker D costs $20,000, and Speaker E costs $10,000. The sum of the speaking fees for all chosen speakers must be within the budget limit.

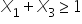2. (AI speaker constraint)

This constraint ensures that at least one speaker specializing in artificial intelligence (AI) is invited.

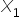Specifically, Speaker A and Speaker C specialize in AI. The sum of the binary decision variables and 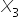must be at least 1, meaning at least one of these speakers must be invited.

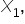
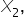
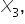
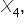3. and 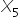in {0,1} (booking decision)

This constraint specifies that each speaker can either be invited (1) or not invited (0).

The binary nature of these variables allows for clear, yes/no decisions regarding the invitation of each speaker, ensuring that the model accurately reflects the decision-making process.