Table of Contents |
As a quick refresher, the fifth step in the experimental method is to analyze the results of a test. This is to determine what the results tell you about the cause-and-effect relationship between two variables.
IN CONTEXT
Imagine you hypothesize that regular watering is required for a tree to grow. To test this, you plant two groups of trees. You water one group regularly and the other less often to see if there’s a difference in growth between the two groups. After a while, you look at the results to determine what they tell you about the cause-and-effect relationship. When comparing these two groups of trees, you will want to compare a single number that describes each group of trees. This number is called a measure of center.
When analyzing data, it’s important to know what the center of a data set is. This helps you summarize and organize the data set so you can convey something meaningful with that data. There are three measures of center that you’ll look at: mean, median, and mode. The mean is the average value for a data set; the median is the middle value, where half of the values are larger, and half are smaller; and the mode is the value that occurs most often.
Measures of center provide you with important information about a data set. They tell you where the middle is located or what a typical value in a data set looks like. However, each measure of center is best for different types of data.
With nominal data, such as gender, the mode is the correct measure of center to use because the only information you can use is how often each value occurs.
For ordinal data, such as first, second, third, etc., the median is the correct measure of center. This is because ordinal data can be put in order, and you can find the middle value by arranging the data from smallest to largest.
For interval or ratio data, either the median or the mean can be used as a measure of center. The mean could be used because the data consists of numbers, while the median could be used because we can arrange the numbers from smallest to largest.
| Data Scale | Example | Measures of Center |
|---|---|---|
| Nominal Data | Gender | Mode |
| Ordinal Data | 1st, 2nd, 3rd,... | Median |
| Interval Data | 45 degrees | Median or Mean |
| Ratio Data | Twice as large | Median or Mean |
Mean, or average is a widely used measure of center. Given a list of numbers, find the mean by adding up all the numbers and then dividing them by how many numbers there are.
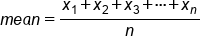
The 1's, 2's, and 3's in the x₁ x₂ x₃—also known as subscripts—indicate the first number in the list, the second number in the list, and so forth, until the last number in the list, marked by the xn. The “n” value in the denominator is the total number of values.
EXAMPLE
The data set below shows the height of the players on the Chicago Bulls basketball team. What height would be considered average or mean height for basketball players on this team?| Player | Height |
|---|---|
| Omer Asik | 84 |
| Carlos Boozer | 81 |
| Ronnie Brewer | 79 |
| Jimmy Butler | 79 |
| Luol Deng | 81 |
| Taj Gibson | 81 |
| Richard Hamilton | 79 |
| Mike James | 74 |
| Kyle Korver | 79 |
| John Lucas III | 71 |
| Joakim Noah | 83 |
| Derrick Rose | 75 |
| Brian Scalabrine | 81 |
| Marquis Teague | 74 |
| C.J. Watson | 74 |
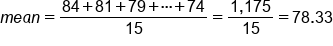
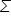. The compact formula of the summation notation is the same as the lengthier formula. Take a moment to make sense of this notation, as it will be used again in this course and is commonly used in statistics.
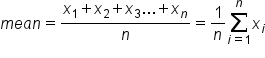
The xᵢ (read as “x subscript i”) is just like the x₁, x₂, and x₃ in the first summation formula. Therefore, this notation means that the value of xᵢ will be the sum of all the x values, starting from the first one (where the i value is 1) and finishing at the “nth,” or last, one. When that is completed, you multiply by 1/n (divide by n), or the total number of values in your dataset.
| Symbol | Pronunciation | Description |
|---|---|---|
| μ | “mew” | Greek letter used to represent the population mean |
|
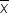
“x-bar” | x with a bar over it; used to represent the sample mean |
|
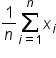
“sigma” | Greek letter used to represent the summation of a series of terms |
IN CONTEXT
Say you grew a crop of pumpkins, and you want to figure out the average, or mean, weight. To do this, you list all the pumpkins by weight, in pounds.
76, 77, 74, 72, 71, 75, 78, 76, 79, 73, 72
How would you figure out what that mean is going to be? Add up all the numbers; this is the sum of x. For this scenario, x = 823. Divide that by the 11 observations. The mean weight is approximately 74.82 pounds.
Had this been a sample of 11 pumpkins from a larger crop of 45, the mean would have been denoted by x bar, or x̄=74.82. If we measured the entire population of 45 pumpkins, the mean would be denoted with μ, the population mean.
To find the median in a list of numbers, first arrange those numbers from smallest to largest. The median is the middle number on your list. If you happen to have an even number of values, simply add the two middle numbers in the list and divide them by two to get the median.
Given a list of ten different numbers, you could simply cross off the first four and the last four:
2, 4, 8, 12, 16, 20, 24, 26, 30, 36
The median is between 16 and 20, so you add them together to figure out their average. They equal 36, which, divided by 2, makes the median 18.
16+20=36
36/2=18
If you have an odd number of observations, you can cross off the numbers to the left and right of the middle number.
3, 5, 9, 11 19, 21, 25
Here, the middle number is 11, and this is the median.
IN CONTEXT
A teacher with 15 students gave an exam, and the scores were:
84, 68, 47, 63, 90, 95, 97, 81, 86, 100, 72, 92, 77
The numbers are not in any particular order.
How do you determine the median?
You need to sort the numbers from smallest to largest. Then you can cross off the numbers on the left and the numbers on the right until you reach the middle.
47, 63, 68, 72, 75, 77, 78,8184, 86, 90, 92, 95, 97, 100
You wind up with your median, which is 81. This means that seven of the 15 students earned less than 81%, and seven earned better than 81% on the exam.
Suppose the teacher forgot that there was a 16th student, and that student happened to get an 85%. You now have an even number of students. How do you determine the median in this case?
Simply reorder the numbers and figure out the average between that eighth and ninth number.
84, 68, 47, 63, 90, 95, 97, 81, 86, 100, 72, 78, 75, 92, 77, 85
The eighth number is 81, and the ninth number is 84. To get the average, add them together and divide by 2. The median here is 82.5%. This means half the class did better than 82.5%, and half the class did worse.
If you have a list of values, the mode is the value that occurs most often on that list. To find the mode, simply count how often each value occurs. It’s possible to have more than one mode, if two or more different values appear equally most often, or no mode if none of the values repeat.
IN CONTEXT
Say you decide to survey 19 households in a neighborhood to see how many cars each household has. Nine of the households have two cars each, while two households don't have any. Four of them only have one car each. Three of them have three, and one household has four cars. The mode is the value that occurs most often, so you can see that the mode in this case is two cars.
Source: THIS TUTORIAL WAS AUTHORED BY DAN LAUB FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.
