In this lesson, you will perform operations on matrices. Specifically, this lesson will cover:
1. Finding the Sum and Difference of Two Matrices
We typically name matrices using capital letters.
For instance, 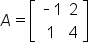 and
and 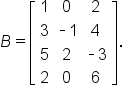
The dimension of a matrix is written 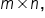 where m is the number of rows and n is the number of columns.
where m is the number of rows and n is the number of columns.
For instance, the dimension of A is 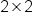 and the dimension of B is
and the dimension of B is 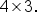
-
Consider the matrix:
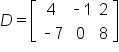
Matrices with the same dimension can be added and subtracted. To add two matrices, add the corresponding entries. To subtract two matrices, subtract the corresponding entries (first minus second).
-
EXAMPLE
Let
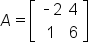
and
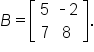
Then,
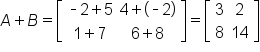
and
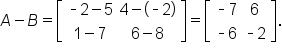
-
Consider the matrices
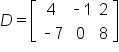
and
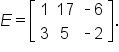
When the numbers in the matrices represent quantities, certain operations can be meaningful too.
-
EXAMPLE
There are three convenience stores in Gambler. For one week, each store's sales were recorded for four items:
- Store I sold 88 loaves of bread, 40 quarts of milk, 12 jars of peanut butter, and 116 pounds of cold cuts.
- Store II sold 105 loaves of bread, 69 quarts of milk, 18 jars of peanut butter, and 150 pounds of cold cuts.
- Store III sold 70 loaves of bread, 30 quarts of milk, no peanut butter, and 50 pounds of cold cuts.
A matrix that could be used to represent this situation is

Quantity of each item is stored in columns; rows correspond to each store.
During the next week, the sales matrix is

The combined sales for both weeks is given by the matrix sum

If you wanted to see the sales gains from one week to the next, you would compute
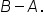
2. Finding Scalar Multiples of Matrices
A scalar is a number that has no dimension; it is simply used as a multiple.
Given a matrix A and a scalar c, the scalar multiple of A is defined as cA, and is obtained by multiplying all entries of matrix A by the scalar c.
Instead of just calling c “a number,” it is important that we distinguish it from matrices since a matrix is a table of numbers.
-
Now, here is one for you to try on your own.
-
Consider the matrix:
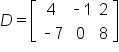
Assuming the matrices have the same dimension, scalar multiplication can be combined with addition and subtraction.
-
EXAMPLE
Given
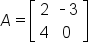
and
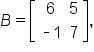
find
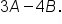
First, perform the scalar multiplications:
-
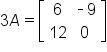 and
and 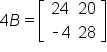
Then,
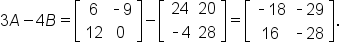
Now, here is one for you to try.
-
Let
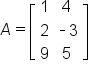
and
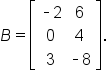
-
- Scalar
- A number that has no dimension, simply used as a multiple.
3. Finding the Product of Two Matrices
3a. The Dimension of a Matrix Product
Given two matrices A and B, their product AB is the result of multiplying the rows of A with the columns of B.
That said, here is what we know about the matrix product AB:
- For AB to be defined, the number of columns in A must be equal to the number of rows in B.
- If A has dimension
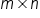 and B has dimension
and B has dimension 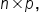 then AB has dimension
then AB has dimension 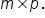
- The products AB and BA are not necessarily equal. That is, matrix multiplication is not commutative.
-
EXAMPLE
Let
A and
B be matrices. If
A has dimension

and
B has dimension
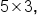
then we know the following:
- The product AB is defined since A has 5 columns and B has 5 rows. The product has dimension
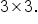
- The product BA is defined since B has 3 columns and A has 3 rows. The product has dimension
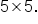
Notice that both products are defined but have different dimensions. This justifies that matrix multiplication is not commutative, since two matrices of different sizes can’t be equal.
-
Let
A and
B be matrices, where A has dimension
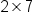
and
B has dimension
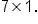
Now, let’s find matrix products.
3b. Calculating Matrix Products
As mentioned earlier, the matrix product AB is found by multiplying each row of A by each column in B. This first example will help to illustrate this.
-
EXAMPLE
Given
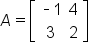
and
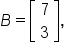
find the matrix product
AB.
First, check the dimensions:
A has dimension
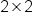
and
B has dimension
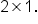
This means that
AB is defined and also has dimension
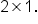
To perform the multiplication, write the product as
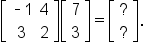
To get the first row, first column entry in the product, multiply the first row of
A by the (first) column of
B.
This is done by multiplying corresponding entries, then adding the products.
That is, multiply
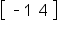
by
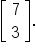
This gives
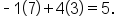
To get the second row, (first) column entry in the product, multiply the second row of
A by the (first) column of
B.
That is, multiply
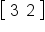
by
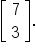
This gives
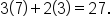
The matrix product
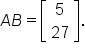
-
In this video, we will find the product
AB where
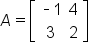
and
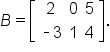
Now, here is one for you to try.
-
Given
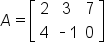
and

Find the matrix product AB.First, make sure that the product is defined:
A has dimension
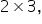
and
B has dimension
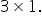
Since the 3’s match, the product is defined, and the result will be a
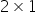
matrix.
Now to find the product, find products of each row from
A with each column of
B.
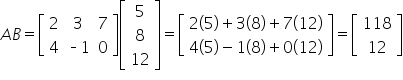
3c. Identity Matrices
The notation 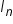 is used to represent the identity matrix with dimension
is used to represent the identity matrix with dimension 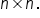
Some examples of identity matrices:
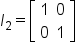
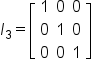
Assuming the matrix product is defined, the product of an identity matrix and a matrix
A in either direction is also equal to
A.
-
Given matrix
A has dimension
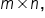
then
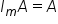
and
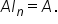
The dimension of
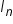
has to be chosen carefully so that the matrix products are defined.
-
EXAMPLE
Consider the matrix:
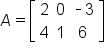
Note that
A has dimension
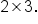
This means that
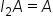
and
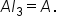
This is illustrated below.

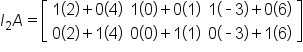
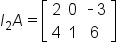
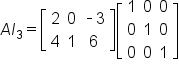
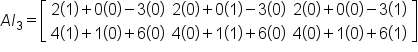
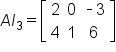
As you can see, the product in both cases is
A.
Now, here is one you can verify.
-
Let
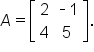
-
- Identity Matrix
- A square matrix in which the entries on the main diagonal (top left to bottom right) are 1s and the rest of the entries are 0s.
In this lesson, you learned that in order to perform operations on matrices, it is important to pay particular attention to the dimension of each matrix. For instance, when
finding the sum and difference of two matrices, addition and subtraction can only be performed when the matrices have the same dimension. You can also
find scalar multiples of matrices by multiplying all entries of a matrix by a scalar, a number that has no dimension and is simply used as a multiple. You also learned that when
finding the product of two matrices, multiplication of matrices is defined only when the number of columns in the first matrix is equal to the number of rows in the second matrix. If this is confirmed, and matrix
A has dimension
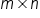
and matrix
B has dimension
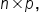
then the
dimension of the matrix product (
AB) is
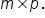
Keep in mind that when
calculating matrix products, matrix multiplication is not commutative. Lastly, you learned about
identity matrices with dimension
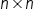
, represented by the notation
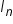
. Since matrices are also a way of organizing information, matrix operations can be used when data is broken into categories.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.
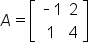 and
and 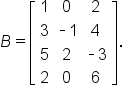
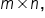 where m is the number of rows and n is the number of columns.
where m is the number of rows and n is the number of columns.
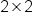 and the dimension of B is
and the dimension of B is 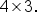
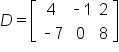
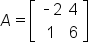 and
and 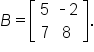
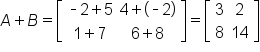 and
and 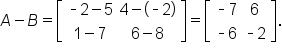
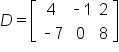 and
and 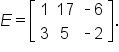
 Quantity of each item is stored in columns; rows correspond to each store.
Quantity of each item is stored in columns; rows correspond to each store.

 If you wanted to see the sales gains from one week to the next, you would compute
If you wanted to see the sales gains from one week to the next, you would compute 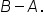
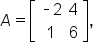 find
find 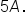
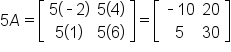
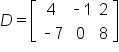
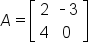 and
and 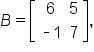 find
find 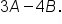
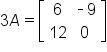 and
and 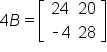
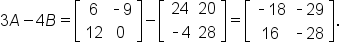
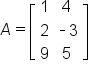 and
and 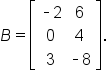
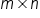 and B has dimension
and B has dimension 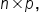 then AB has dimension
then AB has dimension 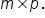
 and B has dimension
and B has dimension 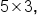 then we know the following:
then we know the following:
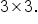
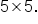
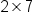 and B has dimension
and B has dimension 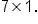
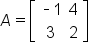 and
and 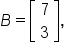 find the matrix product AB.
find the matrix product AB.
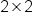 and B has dimension
and B has dimension 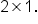 This means that AB is defined and also has dimension
This means that AB is defined and also has dimension 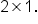
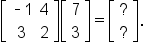
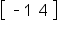 by
by 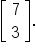 This gives
This gives 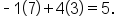
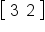 by
by 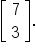 This gives
This gives 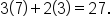
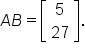
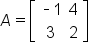 and
and 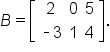
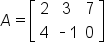 and
and 
 is used to represent the identity matrix with dimension
is used to represent the identity matrix with dimension 
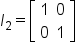
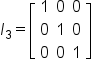
 then
then 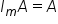 and
and 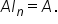 The dimension of
The dimension of 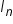 has to be chosen carefully so that the matrix products are defined.
has to be chosen carefully so that the matrix products are defined.
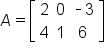
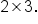 This means that
This means that 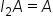 and
and 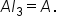 This is illustrated below.
This is illustrated below.

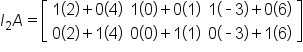
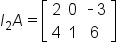
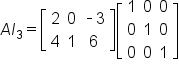
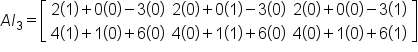
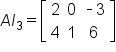
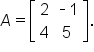
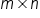 and matrix B has dimension
and matrix B has dimension 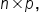 then the dimension of the matrix product (AB) is
then the dimension of the matrix product (AB) is 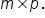 Keep in mind that when calculating matrix products, matrix multiplication is not commutative. Lastly, you learned about identity matrices with dimension
Keep in mind that when calculating matrix products, matrix multiplication is not commutative. Lastly, you learned about identity matrices with dimension 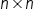 , represented by the notation
, represented by the notation 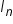 . Since matrices are also a way of organizing information, matrix operations can be used when data is broken into categories.
. Since matrices are also a way of organizing information, matrix operations can be used when data is broken into categories.