Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Literal Equations

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to use inverse operations to rewrite a literal equation. Specifically, this lesson will cover:

Table of Contents

1. Definition of Literal Equation

A literal equation is an equation that has more than one variable. In math, we work with literal equations all the time. For example, the slope–intercept form of a line is a literal equation: 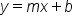y equals m x plus b. This is because it has more than one variable.

term to know
Literal Equation
An equation with more than one variable.

2. Rewriting Literal Equations

Formulas are common literal equations. Formulas relate variables together. For example, we can use a formula to relate the length and width of a rectangle to its area. We can rewrite formulas to create expressions for other variables in the equation.

EXAMPLE

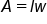
A equals l w Formula for the area of a rectangle
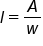
l equals A over w Divide by w; expression for length
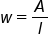
w equals A over l Divide by l, expression for width

We can rewrite literal equations to express other variables by applying inverse operations. More specifically, we look at what operations are being applied to the variable we wish to isolate, as well as in what order they are being applied. To isolate the variable, we apply the inverse operations in reverse order. This is shown below with several common formulas:

EXAMPLE

Use the formula for the area of a circle and solve for the radius, r.

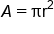
A equals πr squared Formula for the area of a circle
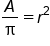
A over straight pi equals r squared Divide both sides by straight pi
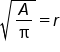
square root of A over straight pi end root equals r Take square root of both sides

EXAMPLE

Use the formula for the distance and solve for rate, r.

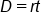
D equals r t Formula for distance, rate, and time
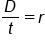
D over t equals r Divide both sides by t

EXAMPLE

Use the formula for the distance and solve for time, t.

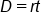
D equals r t Formula for distance, rate, and time
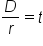
D over r equals t Divide both sides by r

EXAMPLE

Use the Pythagorean Theorem and solve for one side length,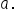 a.

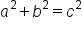
a squared plus b squared equals c squared Pythagorean Theorem
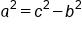
a squared equals c squared minus b squared Subtract 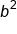b squared from both sides
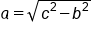
a equals square root of c squared minus b squared end root Take square root of both sides

EXAMPLE

Use the Pythagorean Theorem and solve for the second side length, b.

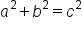
a squared plus b squared equals c squared Pythagorean Theorem
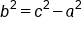
b squared equals c squared minus a squared Subtract 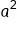a squared from both sides
b equals square root of c squared minus a squared end root Take square root of both sides

summary
The definition of literal equations are equations that have more than one variable. Formulas are literal equations and are used often in mathematics. Depending on what kind of information you are given, you may wish to rewrite literal equations, or express the equations and formulas in different ways.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Literal Equation

An equation with more than one variable.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.