Table of Contents |
Before we move on and introduce inequalities, let’s take a look at interval notation to get a better understanding of endpoints. An endpoint is where a range of values starts or ends.
On a number line, we define specific intervals on the number line using symbols.
For example, let’s look at the interval on the number line below that shows a highlighted range of values:

If we examine the highlighted portion of the number line, we can see that the highlighted portion starts at negative 2 and ends at positive 3. These are the endpoints of this interval: -2 and +3. Note there is an open circle at -2. This means that the interval includes the numbers between -2 and 3, but the interval does not include -2. So, -1, -1.7, and -1.99 are within the interval, but -2 is not within the interval.
We can also see that there is a filled-in circle or a closed circle at the positive 3 on the number line. This means that the interval ends at 3 and the endpoint 3 is included in the interval. So, 1, 2.95, and 3 are all within the interval.
| Open and Closed Circles for Intervals on a Number Line | |
| Endpoint is included in interval (closed circle) | Endpoint is not included in interval (open circle) |
|---|---|

|

|
So, how would we write this interval between -2 and +3 without showing a picture on the number line? We need a few more symbols to express whether the endpoint is included within the interval or not. These include square brackets and parentheses.
| Symbols for Notating Intervals | |
| Endpoint is included in interval (relates to closed circles) | Endpoint is not included in interval (relates to open circles) |
|---|---|
| [ or ] | ( or ) |
Square brackets correspond to the closed circles on the number line. They indicate that the endpoint is included in the interval. The parentheses (or rounded brackets) are used when there are open circles on the number line, and the endpoint is not included in the interval.
EXAMPLE
Write the highlighted range on the number line in interval notation.
Intervals with one endpoint are written quite differently.


Sometimes, we want to describe numbers that fall into two or more non-overlapping intervals. For example, a person’s resting heart rate per minute might be of concern if it is below 40 beats per minute or above 100 beats per minute.
Here is the shaded number line for this situation. (Note that the left-hand interval starts at 0 since we can’t have a negative number of heartbeats).

How would we represent this using interval notation?
To do so, we need to define the union of two intervals, which can also be thought of as sets of numbers.
If there is more than one interval, we use the union symbol (⋃) between the intervals in interval notation.
In our problem, note that the first interval is written 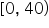 and the second is written
and the second is written 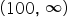 . Then, the interval notation that includes all the numbers is
. Then, the interval notation that includes all the numbers is 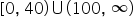 .
.
EXAMPLE
Use the number line below and write the interval in interval notation.
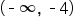 and the second interval is
and the second interval is 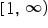 . To accept both intervals as solutions for x, we use the symbol for union,
. To accept both intervals as solutions for x, we use the symbol for union, 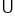 , to connect or join the two intervals together. To complete our solution in interval notation, we have
, to connect or join the two intervals together. To complete our solution in interval notation, we have 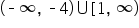 .
.
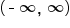 is used to represent the entire real number line.
is used to represent the entire real number line. 
So far in this course, we have only talked about equalities; in other words, 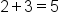 or
or  . In this lesson, we will cover inequalities. An inequality is a mathematical statement to show that one quantity is greater than or less than another quantity. The following outlines the different inequality symbols and their meanings:
. In this lesson, we will cover inequalities. An inequality is a mathematical statement to show that one quantity is greater than or less than another quantity. The following outlines the different inequality symbols and their meanings:
| Symbol | Translation | Example |
|---|---|---|
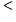
|
Less than |
 3 is less than 5 |
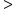
|
Greater than |
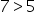 7 is greater than 5 |
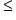
|
Less than or equal to |
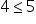 4 is less than or equal to 5 |
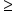
|
Greater than or equal to |
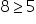 8 is greater than or equal to five |
Inequalities are used in statistics, business, economics, and optimization when comparing values to each other. As you likely know, young children seem to master inequalities at an irritatingly early age. What happens if you give one child three candy bars and the other, two? Of course, the child with the two candy bars will complain that the other child “has more.”
Inequalities are also used in algebraic problems. For example, if we have an expression such as 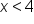 , this means our variable can be any number smaller than 4 such as -2, 0, 3, 3.9 or even 3.999999999, as long as it is smaller than 4.
, this means our variable can be any number smaller than 4 such as -2, 0, 3, 3.9 or even 3.999999999, as long as it is smaller than 4.
Initiative: Why Employers Care |
When looking at number lines with a range of highlighted values, we can write the range of values a couple of different ways: in a format called set builder notation, and in interval notation. We will use inequalities to help us write the intervals in set builder notation. Let’s look at the symbols so far and add in the inequality symbols also.
| Endpoint Symbols for Notating Intervals | |
| Endpoint IS included in interval | Endpoint IS NOT included in interval |
|---|---|

|

|
| [ or ] | ( or ) |
 or or 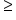
|
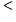 or or 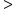
|
If we add inequalities to the chart of endpoint symbols, we see that the less than (<) and the greater than (>) symbols indicate that the endpoint is not included in the interval. We see that the less than or equal to (≤) or greater than or equal to (≥) symbols do include the endpoints in the interval. If we have an expression such as  greater than or equal to -2, this means our variable can be any number greater than or equal to -2, such as 5, 0, -1, -1.9999, or even -2.
greater than or equal to -2, this means our variable can be any number greater than or equal to -2, such as 5, 0, -1, -1.9999, or even -2.
In set builder notation, we can use inequalities to help us write the interval in set builder notation. In set builder notation, we define the range of values as a set of numbers, and we use curly brackets to define the set, with a description of what is to be included in the set.
EXAMPLE
Write the highlighted range in set builder notation.
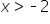 and
and 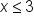 .
.
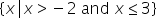 . This reads as “all x-values, such that x is greater than (but not including) -2 but x is also less than and can include 3.”
. This reads as “all x-values, such that x is greater than (but not including) -2 but x is also less than and can include 3.”

EXAMPLE
Consider the interval highlighted on the number line below.
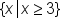 .
.
 can be any number in the highlighted range that is greater than or equal to 3.
can be any number in the highlighted range that is greater than or equal to 3.
Let’s consider the same example from before where there were two intervals on the number line.
EXAMPLE
Use the number line below and write the interval in set builder notation.
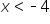 . We also have
. We also have 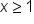 .
.
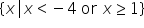 . We use the connecting word "or" because values that fit within either inequality statement will fit the number line solution.
. We use the connecting word "or" because values that fit within either inequality statement will fit the number line solution.
Let's practice writing in set builder notation and interval notation, using number line solutions.
EXAMPLE
Use the number line below and write the interval in set builder notation and interval notation.
| Notation | Explanation | Solution |
|---|---|---|
| Set Builder Notation |
We notice that all values from 2 to positive infinity are highlighted. In set builder notation, we would write this as 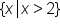 . Note that our inequality symbol does not include the exact value of 2. . Note that our inequality symbol does not include the exact value of 2.
|
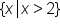
|
| Interval Notation |
In interval notation, this is written as 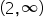 . Note that we use a parenthesis to the left of 2, and also a parenthesis to the right of infinity symbol. . Note that we use a parenthesis to the left of 2, and also a parenthesis to the right of infinity symbol.
|
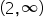
|

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.