Table of Contents |
When solving an equation for a variable, our main goal is to isolate a variable. In other words, we want to get the variable by itself on one side of the equation, with all other expressions on the other side of the equals sign. In this process, we must always remember that if we perform an operation on one side of the equal sing, we must do the same on the other side of the equal sign.
EXAMPLE
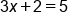 
|
Solve for x by first subtracting 2 from both sides |
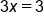 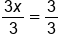
|
Divide both sides by 3 |
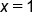
|
Our Solution |
When isolating a variable, we need to keep the following in mind:
| Operation | Inverse Operation |
|---|---|
| Addition | Subtraction |
| Subtraction | Addition |
| Multiplication | Division |
| Division | Multiplication |
| Powers | Roots |
| Roots | Powers |
A good rule of thumb is to isolate the outermost operations surrounding the variable first, working our way inwards until we isolate the variable.
EXAMPLE
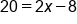 
|
Solve for x by first adding 8 to both sides |
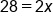 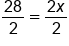
|
Divide both sides by 2 |
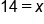
|
Our Solution |
Sometimes when we try to isolate a variable, it may be better to simplify the equation before we perform any inverse operations.
EXAMPLE
Suppose we want to solve for x in the following equation: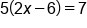 .
.
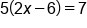
|
Solve for x by distributing 5 into 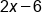
|
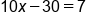
|
Add 30 to both sides |
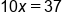
|
Divide both sides by 10 |
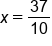
|
Express 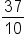 as a decimal as a decimal
|
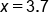
|
Our Solution |
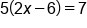
|
Solve for x by dividing both sides by 5 |
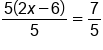
|
5's on the left side cancel, leaving 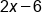 ; express ; express 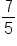 as a decimal as a decimal
|

|
Add 6 to both sides |
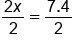
|
Divide both sides by 2 |
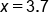
|
Our Solution |
Let's look at another example where combining like terms before attempting to isolate the variable can be helpful:
EXAMPLE
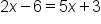
|
Solve for x by first move the x terms to one side |

|
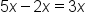
|
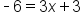
|
Move constant terms to one side |
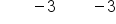
|
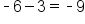
|
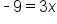
|
Divide both sides by 3 |
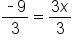
|
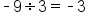
|
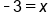
|
Our Solution |
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License