Table of Contents |
Consider the function 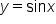 shown in the figure.
shown in the figure.
Since the function is not one-to-one, its inverse is not a function.
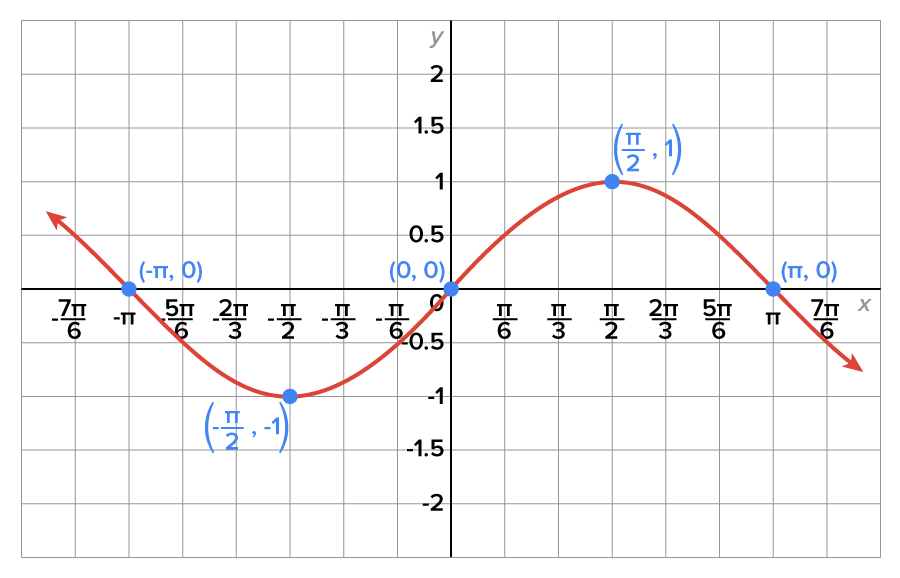
The graph below shows the function 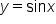 on the restricted domain
on the restricted domain 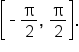
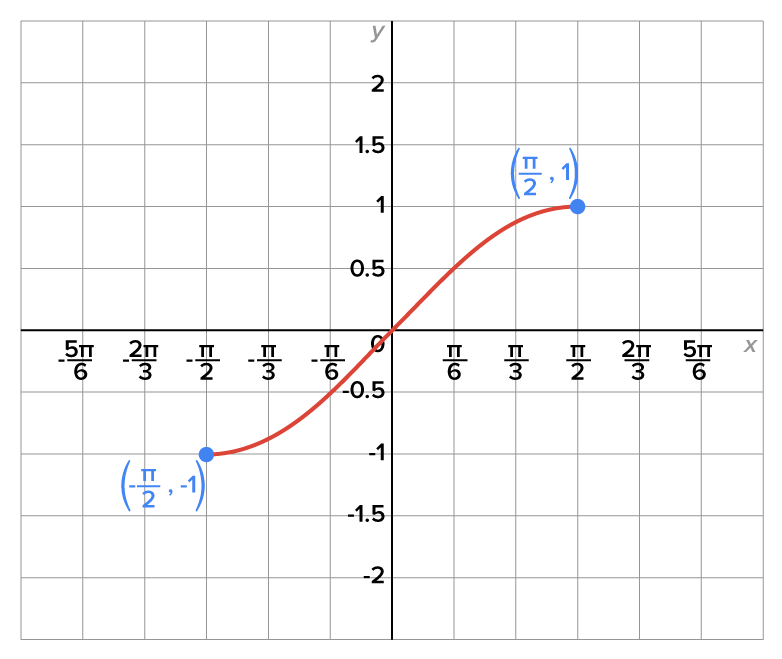
On the restricted domain, 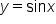 is one-to-one, and the range is
is one-to-one, and the range is 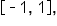 which is the same as the unrestricted sine function.
which is the same as the unrestricted sine function.
Recall that the domain of a function is the range of its inverse function, and the range of a function is the domain of its inverse function.
Therefore, on the restricted domain, the inverse of the sine function has domain 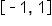 and range
and range 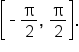
To find the inverse of 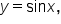 first interchange x and y to get
first interchange x and y to get 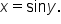 Since there is no mathematical operation that can be used to solve for y, we define the inverse sine function as follows.
Since there is no mathematical operation that can be used to solve for y, we define the inverse sine function as follows.
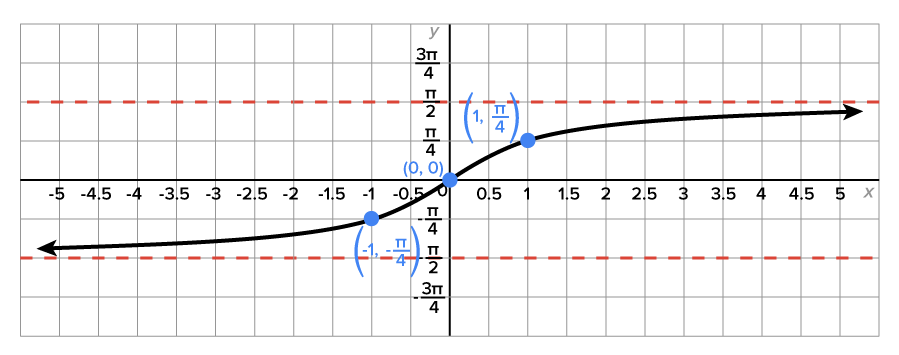
The inverse sine function, or the function 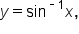 is the value of y such that
is the value of y such that 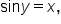 where
where 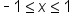 and
and 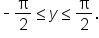
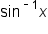 is NOT an exponent. A common mistake is to rewrite
is NOT an exponent. A common mistake is to rewrite 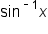 as
as 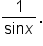 The notation
The notation 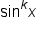 means
means 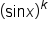 when
when 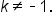
This means that the inverse sine function receives a number between -1 and 1 as input, and returns an angle between 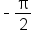 and
and 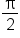 as its output.
as its output.
We know that 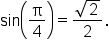 Since
Since 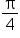 is between
is between 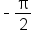 and
and 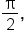 it follows that
it follows that 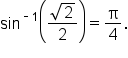
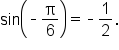
The graph of 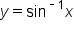 is shown below.
is shown below.
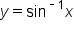 is the value of y such that
is the value of y such that 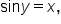 where
where 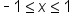 and
and 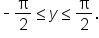
Consider the function 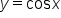 shown in the figure.
shown in the figure.
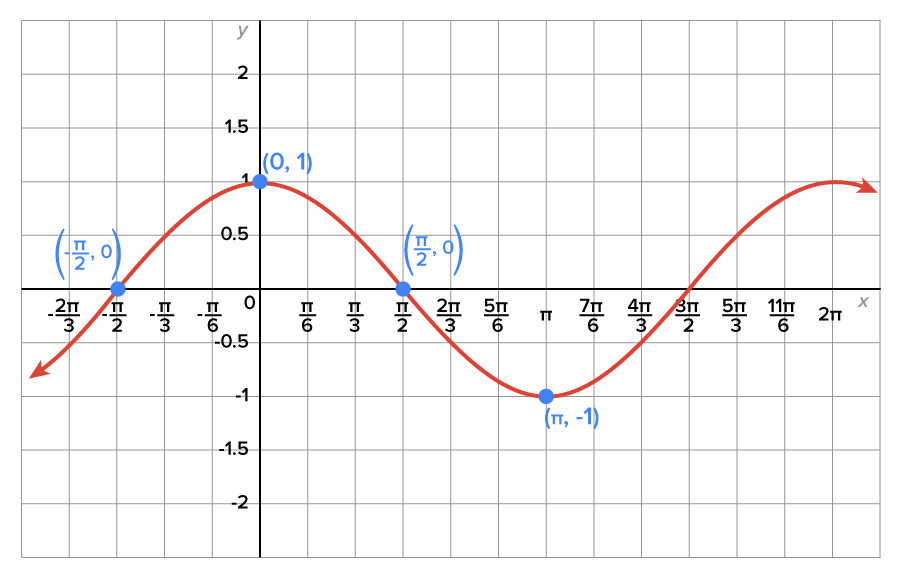
Since the function is not one-to-one, its inverse is not a function.
The graph below shows the function  on the restricted domain
on the restricted domain 
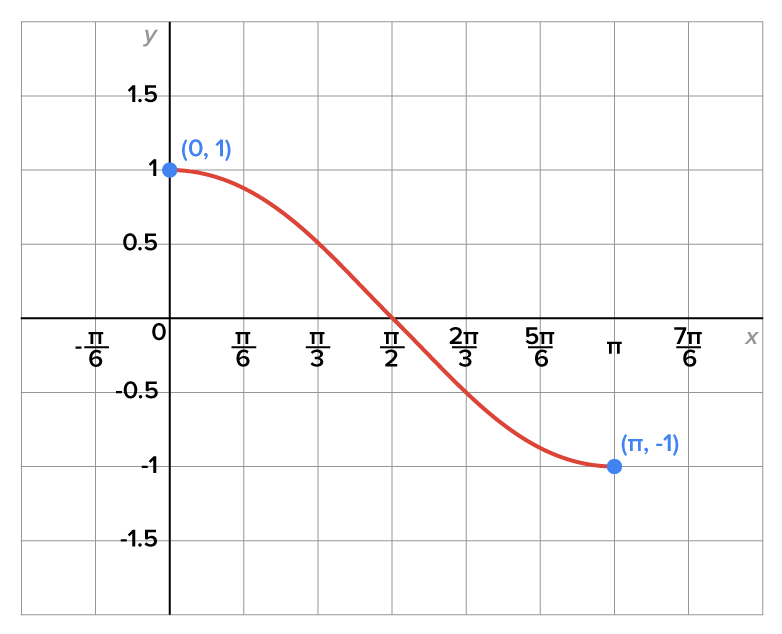
On the restricted domain, 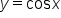 is one-to-one, and the range is
is one-to-one, and the range is 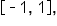 which is the same as the unrestricted cosine function.
which is the same as the unrestricted cosine function.
Therefore, its inverse function has domain 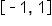 and range
and range 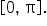
To find the inverse of  first interchange x and y to get
first interchange x and y to get 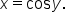 Since there is no mathematical operation that can be used to solve for y, we define the inverse cosine function as follows.
Since there is no mathematical operation that can be used to solve for y, we define the inverse cosine function as follows.
The inverse cosine function, or the function 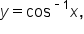 is the value of y such that
is the value of y such that 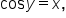 where
where 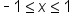 and
and 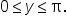
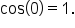
The graph of 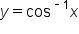 is shown below.
is shown below.
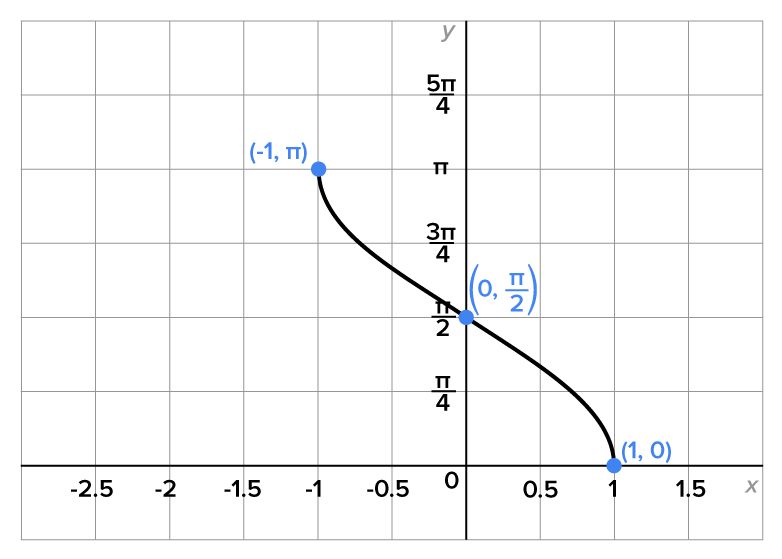
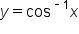 is the value of y such that
is the value of y such that 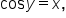 where
where 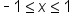 and
and 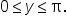
Consider the function 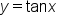 shown in the figure.
shown in the figure.
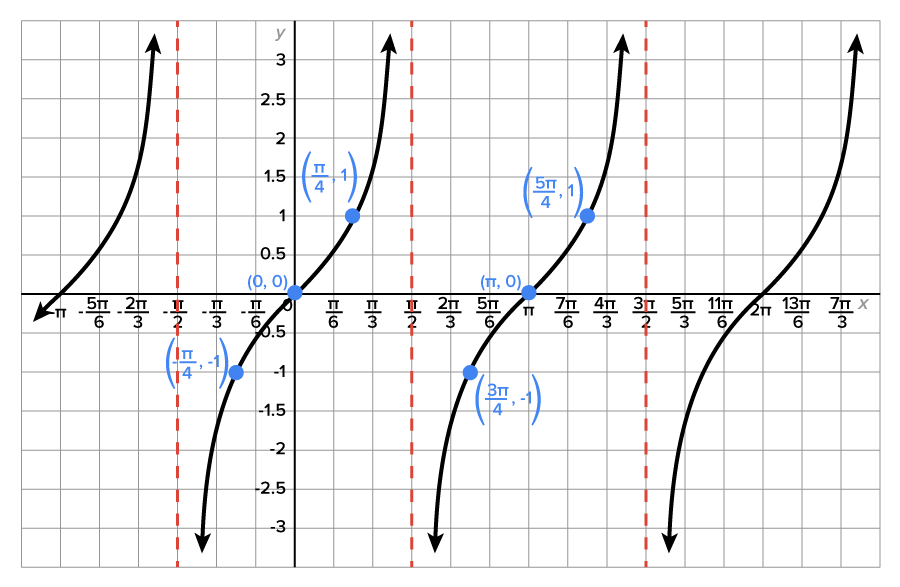
Since the function is not one-to-one, its inverse is not a function.
The graph below shows the function 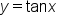 on the restricted domain
on the restricted domain 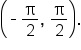
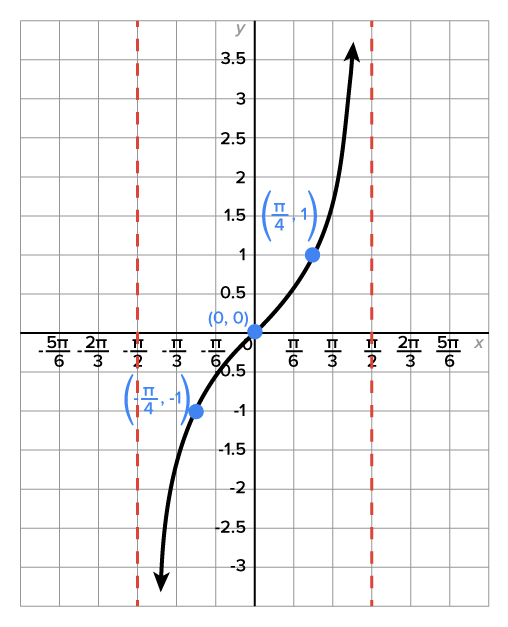
On the restricted domain, 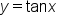 is one-to-one, and the range is
is one-to-one, and the range is 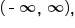 which matches the range of the unrestricted tangent function.
which matches the range of the unrestricted tangent function.
Therefore, its inverse function has domain 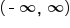 and range
and range 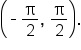
To find the inverse of 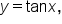 first interchange x and y to get
first interchange x and y to get 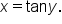 Since there is no mathematical operation that can be used to solve for y, we define the inverse tangent function as follows.
Since there is no mathematical operation that can be used to solve for y, we define the inverse tangent function as follows.
The inverse tangent function, or the function 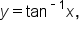 is the value of y such that
is the value of y such that 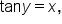 where x is any real number and
where x is any real number and 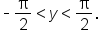
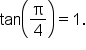
The graph of 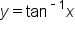 is shown below.
is shown below.
 and
and  The “arc” prefix is used to show that the function returns the length of the arc (in radians) for the corresponding trigonometric function and argument.
The “arc” prefix is used to show that the function returns the length of the arc (in radians) for the corresponding trigonometric function and argument.
The output of an inverse trigonometric function is an angle. The input of an inverse trigonometric function is often called the argument of the function. You may recall we used this word to describe the input of a logarithmic function.
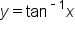 is the value of y such that
is the value of y such that 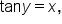 where x is any real number and
where x is any real number and 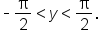
When the argument of an inverse sine or cosine function is one of the special values of the corresponding trigonometric function (positive or negative), the unit circle can be used to evaluate the function exactly. A unit circle is shown below.
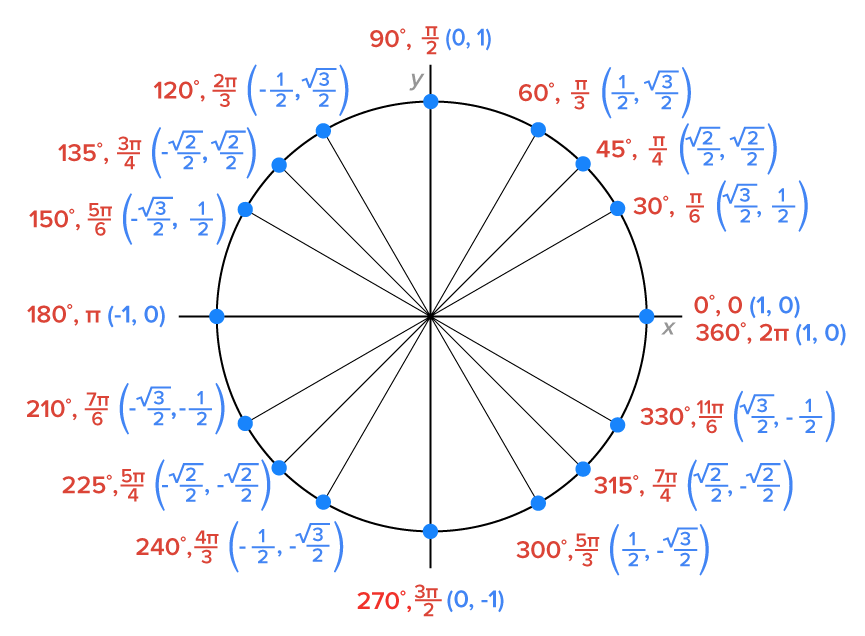
EXAMPLE
Evaluate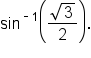
 such that
such that 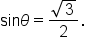
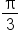 and
and 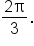
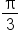 is in the interval
is in the interval 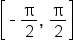 , but
, but 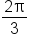 is not in the interval
is not in the interval 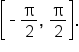
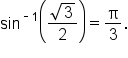
When the argument of the inverse trigonometric function is negative (and in the domain of the function), you could still use the unit circle, but reference angles can also be used to find the value of the inverse trigonometric function, keeping in mind the range of the inverse trigonometric function.
EXAMPLE
Find the exact value of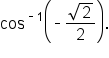
 so that
so that 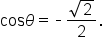 On the first revolution of the unit circle, there are two possible answers:
On the first revolution of the unit circle, there are two possible answers: 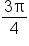 and
and 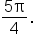
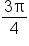 is in the interval
is in the interval 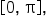 but
but 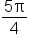 is not in the interval
is not in the interval 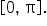
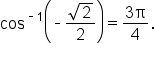
EXAMPLE
Evaluate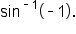
 so that
so that 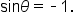 On the first revolution of the unit circle, there is one possible answer:
On the first revolution of the unit circle, there is one possible answer: 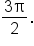 Since
Since 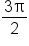 is not in the range of the inverse sine function, subtract
is not in the range of the inverse sine function, subtract 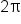 to get an angle coterminal to
to get an angle coterminal to 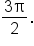 The result is
The result is 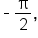 which is in the interval
which is in the interval 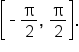
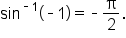
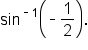
Refer back to the special values of the tangent function. Knowing these is very helpful to evaluate the inverse tangent function.
EXAMPLE
Evaluate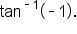
 so that
so that 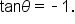 On the first revolution of the unit circle, there are two possible answers:
On the first revolution of the unit circle, there are two possible answers: 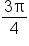 and
and 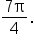 Neither angle is in the interval
Neither angle is in the interval 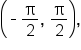 but since
but since 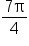 is in quadrant IV, subtract
is in quadrant IV, subtract 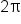 to get an angle coterminal to it. The result is
to get an angle coterminal to it. The result is 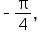 which is in the interval
which is in the interval 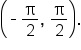
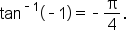

On your calculator, usually above the buttons SIN, COS, and TAN, you should see three labels marked 
 and
and 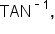 which are used to evaluate trigonometric functions. They are usually 2nd functions, meaning you might need to press the “Shift” or “2nd” keys to access them.
which are used to evaluate trigonometric functions. They are usually 2nd functions, meaning you might need to press the “Shift” or “2nd” keys to access them.
As long as the input value is in the domain of the inverse trigonometric function that you use, the calculator will return a value in decimal form.
If your calculator is in radian mode, the inverse trigonometric functions will return an angle in radian form. Most calculators will return an approximate form, but some have the capability to return the exact form, especially if the input value is one of the special values discussed earlier.
If your calculator is in degree mode, the inverse trigonometric functions will return an angle measured in degrees.
For example, consider the expression 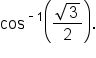
When in radian mode, your calculator most likely will return the value 0.5236 (this value is rounded to four decimal places).
When in degree mode, your calculator will return the value 30, which means 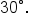
On the other hand, consider the expression 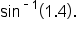
In either degree or radian mode, your calculator will return an error message. Since 1.4 is not in the domain of the inverse sine function, there is no output value for an input value of 1.4.
Up to this point, we could only find unknown angles of a right triangle if one other angle was known. Now that we’ve learned about inverse trigonometric functions, we can find an angle associated with the ratio of two sides.
EXAMPLE
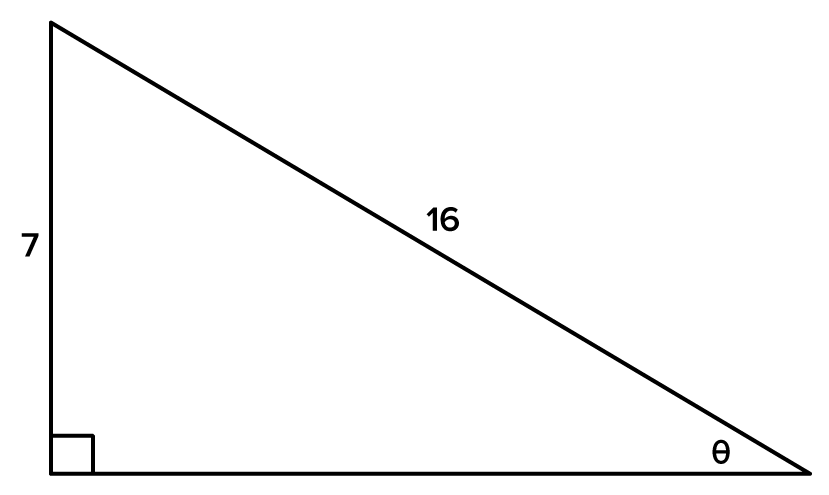
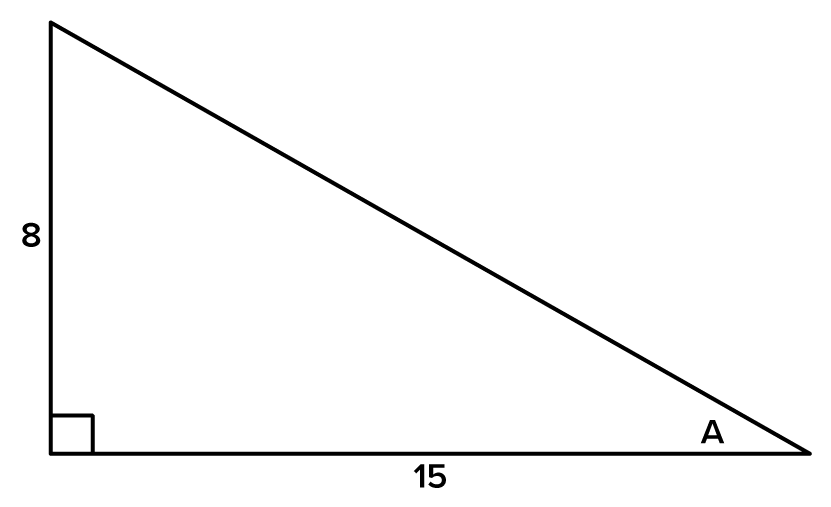
Consider the triangle below, and find the angle to the nearest degree.
to the nearest degree.
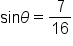
|
Referencing the angle 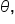 its opposite side and the hypotenuse are known. Therefore, the sine function should be used to relate the sides and the angle. its opposite side and the hypotenuse are known. Therefore, the sine function should be used to relate the sides and the angle.
|
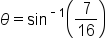
|
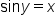 means means 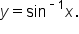
|
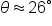
|
Approximate the value using a calculator, in degree mode. |
These ideas can also be applied to real-world problems.
EXAMPLE
A truss for the roof of a house is constructed using two identical right triangles. Each has a base of 12 feet and height 4 feet, as shown in the figure.
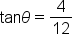
|
Let  be the angle adjacent to the side with length 12 feet. Using this angle as a reference, the sides opposite and adjacent to the angle are known, which means tangent is the best choice to relate the sides and the angle. be the angle adjacent to the side with length 12 feet. Using this angle as a reference, the sides opposite and adjacent to the angle are known, which means tangent is the best choice to relate the sides and the angle.
|
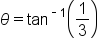
|
Reduce 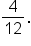 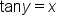 means means 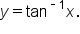
|
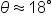
|
Approximate the angle using a calculator. |
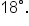
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.