Table of Contents |
As we graph lines, we will want to be able to identify different properties of the lines we graph. One of the most important properties of a line is its slope. Slope is a measure of steepness. A line with a large slope, such as 25, is very steep. A line with a small slope, such as 0.10 is very flat. We will also use slope to describe the direction of the line. A line that goes up from left to right will have a positive slope and a line that goes down from left to right will have a negative slope.
As we measure steepness, we are interested in how fast the line rises compared to how far the line runs. For this reason we will describe slope as the fraction 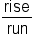 . Rise would be a vertical change, or a change in the y-values. Run would be a horizontal change, or a change in the x-values. So another way to describe slope would be the fraction
. Rise would be a vertical change, or a change in the y-values. Run would be a horizontal change, or a change in the x-values. So another way to describe slope would be the fraction 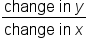 .
.
It turns out that if we have a graph, we can draw vertical and horizontal lines from one point to another to make what is called a slope triangle. The sides of the slope triangle give us our slope.
EXAMPLE
Find the slope of the following line.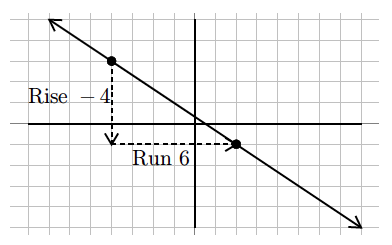
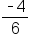 . Reduce the fraction to get
. Reduce the fraction to get 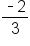 , so the slope is
, so the slope is 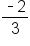 .
.
EXAMPLE
Find the slope of the following line.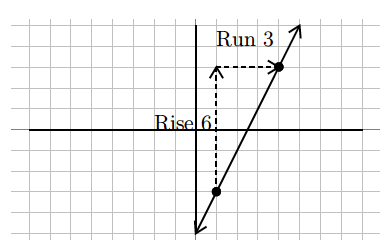
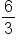 . This fraction reduces to 2, so the slope is 2.
. This fraction reduces to 2, so the slope is 2.
We can find the slope of a line through two points without seeing the points on a graph. We can do this using a slope formula. If the rise is the change in y-values, we can calculate this by subtracting the y-values of a point. Similarly, if the run is a change in the x-values, we can calculate this by subtracting the x-values of a point. So we can say the following:
The slope of a line through 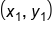 and
and 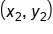 is
is 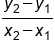 .
.
When mathematicians began working with slope, it was called the modular slope. For this reason, we often represent the slope with the variable m. Now we have the following for slope.
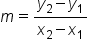
There are two special lines that have unique slopes that we need to be aware of.
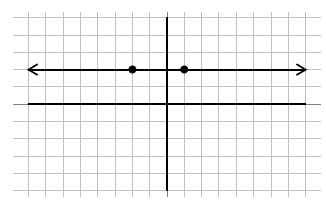
The line below is a horizontal line. For this line, the slope is not steep at all, in fact, it is flat. Therefore it has a zero slope.
This next line is a vertical line. For this line, the slope can’t get any steeper. It is so steep that there is no number large enough to express how steep it is so this is an undefined slope.
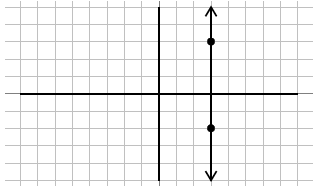
As you can see there is a big difference between having a zero slope and having no slope or an undefined slope. Remember, slope is a measure of steepness.
There is an interesting connection between the slope of lines that are parallel and the slope of lines that are perpendicular (meet at a right angle).
| Type of Line | Description | Slope | Example |
|---|---|---|---|
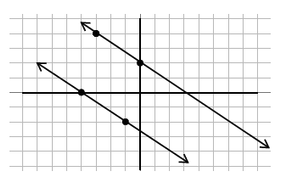
| Parallel | Lines that never intersect | Identical slopes |
|
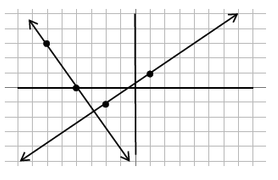
| Perpendicular | Lines that intersect at a right angle | Opposite reciprocal slopes |
|
As the above graphs illustrate, parallel lines have the same slope, and perpendicular lines have opposite (one positive, one negative). In fact, perpendicular lines have reciprocal (flipped fraction) slopes. We can use these properties to make conclusions about parallel and perpendicular lines.
Let's take a further look at the example above with perpendicular lines.
EXAMPLE
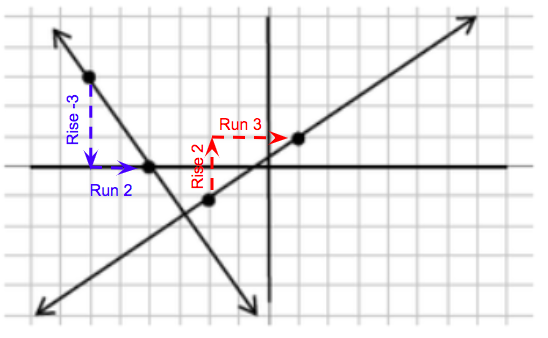
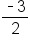 . The other line that is perpendicular has a rise of 2 and a run of 3, so the slope of this line is
. The other line that is perpendicular has a rise of 2 and a run of 3, so the slope of this line is 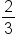 . These two slopes are opposite reciprocals. They are opposite meaning one slope is positive while the other is negative. The slopes are also reciprocals meaning their fractions are flipped.
. These two slopes are opposite reciprocals. They are opposite meaning one slope is positive while the other is negative. The slopes are also reciprocals meaning their fractions are flipped.
See how slopes of parallel and perpendicular lines compare in the following table:
| Slope of Line 1 | Slope of Line 2 | Relationship | Explanation |
|---|---|---|---|
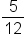
|
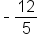
|
Perpendicular |
The reciprocal of 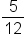 is is 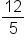 , and then make it negative! , and then make it negative!
|
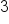
|
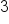
|
Parallel | Since they both have the same value for the slope, they are parallel lines. |
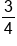
|
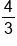
|
Neither | Although the fractions are reciprocals, they are not opposites. |
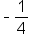
|
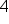
|
Perpendicular |
The reciprocal of 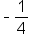 is is 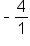 , or just 4. Then make it positive! , or just 4. Then make it positive!
|
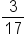
|
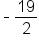
|
Neither | Although they are opposites (one positive, one negative), these fractions are not reciprocals. |
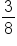
|
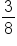
|
Parallel | Since they both have the same value for the slope, they are parallel lines. |
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License