Table of Contents |
There are a variety of different number types that make up our real number system. Numbers such -2, 7.8, and 1/3 can be categorized into different groups within the set of all real numbers. Let's first define real numbers. A real number is any type of number that can be placed on a number line.
We are going to illustrate different types of real numbers using the picture below:
We can refer to this image as representing the universe of all real numbers. What numbers do you see? Nothing? Or Everything? This picture is blank (aside for the title "Set of all Real Numbers") simply because everything that fits within this picture means that it exists within the universe of real numbers. As you move down you will see different types of real numbers appear in the picture. The first type of real number we are going to talk about is an integer.
Integers come up all the time in math, so let's define what an integer is. An integer is any positive or negative whole number and zero.
For example: {...-3, -2, -1, 0, 1, 2, 3...}. Notice that zero is also an integer.
IN CONTEXT
Think about integers as whole dollars — and no cents. You earned a $5 bill for walking a neighbor’s dog (5) or you lost a $10 bill during that walk (-10). No coins were earned or lost. We’ll talk about coins or “decimals” later.
Let's include integers on our picture:
Next, we get into two very special types of numbers, the first being rational numbers. Looking at the word "rational" we see "ratio." A rational number is a ratio of two integers, expressed as a/b.
In other words, a rational number is a fraction. But what is a fraction? A fraction is a part of a whole,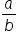 
. The number at the top of the fraction (a) is called the numerator. The number at the bottom of the fraction (b) is called the denominator.
Think of a fraction as a piece of a pie or how many slices of pizza you ate last night. For example, let’s look at this pizza:
The total amount of pieces the pizza was cut into is called the denominator. The amount of pieces you ate is called the numerator. So for this example, the pizza was cut into 8 pieces and you ate 3. The fraction for pieces eaten would be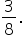 
Rational numbers could also be decimals. But not just any decimal — a decimal that terminates (ends), or repeats itself. For example, we have 4 quarters, which makes a dollar. If I take 1 quarter, we can write this as the fraction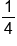 
. We know that one quarter is equal to $0.25. Therefore, 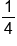can also be written as a decimal, 0.25. We’ll cover how to convert any fraction into a decimal in a later challenge, but for this example, you can see that 0.25 is a terminating decimal — in other words, it ends.
Not all rational numbers need to have a decimal that ends like the example above. It could also be a decimal that repeats such as .03333…. Think about it this way: as long as you can show someone what the full decimal is, it’s a rational number. If you can’t, that’s an irrational number.
Let's place rational numbers on our diagram:
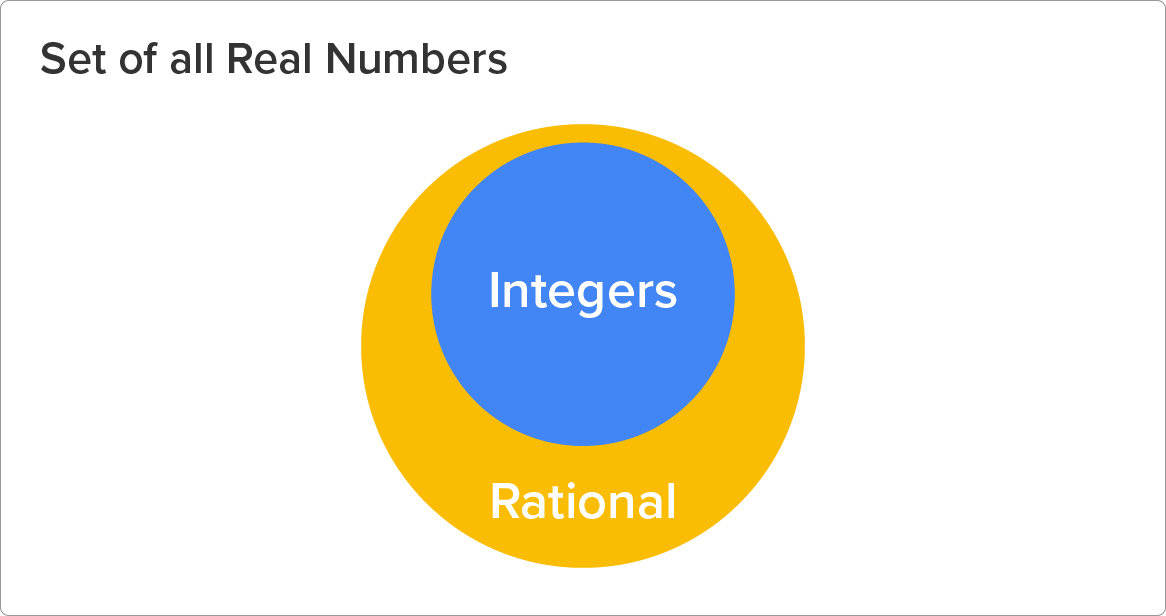
You’ll notice that the integer circle is inside of the rational circle. Why? All integers could be considered rational. For example, the fraction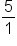 
could be 5, or $5.00 is still considered $5. However, not all rational numbers are integers. For example, 
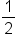is not a whole number — it’s a part of a whole.
There is one other type of real number that we would like to include on our picture, and it breaks the pattern we have built up so far. This number type is called irrational numbers. Irrational numbers are numbers which cannot be represented as a ratio of integers.
What does this look like in our picture?
Irrational numbers still exist within our set of real numbers, but they do not enclose integers or rational numbers. Why? Because they are not created using a ratio of integers.
Now let's look at the decimal patterns of irrational numbers. Pi (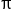
) is a common irrational number. Notice that we use a special symbol for this number. Pi is approximately 3.14159. This is only an approximation of pi because the decimal pattern never stops, and there is no recognizable decimal pattern. So a characteristic of an irrational number is that the decimal pattern does not terminate (keeps going forever and ever), and it does not repeat (there is no repeating decimal pattern).
Problem Solving: Skill in Action |
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.
