Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Introduction to Quadratic Equations

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to identify a parabola given a vertex and solution set. Specifically, this lesson will cover:

Table of Contents

1. Quadratics as Second Degree Polynomials

A quadratic is a second-degree polynomial, which means that in the expression of a quadratic, there will be no more than 2 x-terms being multiplied together. In expanded form, the highest exponent you will see is 2, and in factored form, there will only be two factors of x.

EXAMPLE

The expression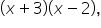 open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses comma which in expanded form is 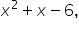x squared plus x minus 6 comma is a quadratic.

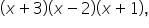The expression open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses open parentheses x plus 1 close parentheses comma which in expanded form is 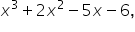x cubed plus 2 x squared minus 5 x minus 6 comma is not a quadratic.

In general, if there are two factors containing x, the expression is quadratic. Otherwise, the expression is not quadratic.

term to know
Quadratic
A second-degree polynomial, with an x-squared term as its highest degree term.

2. Forms of Quadratic Equations

There are several different ways to write a quadratic equation. We are going to cover standard form, vertex form, and factored form:

2a. Standard Form

A quadratic written in the form 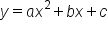y equals a x squared plus b x plus c is considered in standard form, which is the expanded form of the equation. As we will learn, the coefficients a, b, and c are related to special properties.

formula to know
Standard Form
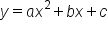
y equals a x squared plus b x plus c

2b. Vertex Form

Vertex form is ideal for graphing quadratic equations because it provides information about the parabola's vertex readily in its equation. The variables h and k represent the x- and y-coordinates to the vertex. The vertex is the point 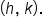left parenthesis h comma space k right parenthesis.

formula to know
Vertex Form
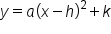
y equals a left parenthesis x minus h right parenthesis squared plus k

2c. Factored Form

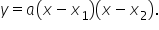
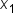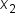A quadratic equation in factored form is written as y equals a open parentheses x minus x subscript 1 close parentheses open parentheses x minus x subscript 2 close parentheses.

In this form, a is any nonzero number. The numbers x subscript 1 and x subscript 2 are the locations of the x-intercepts of the graph.

formula to know
Factored Form
y equals a open parentheses x minus x subscript 1 close parentheses open parentheses x minus x subscript 2 close parentheses

EXAMPLE

Consider the quadratic equation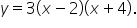 y equals 3 open parentheses x minus 2 close parentheses open parentheses x plus 4 close parentheses.

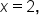
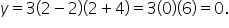When x equals 2 comma y equals 3 open parentheses 2 minus 2 close parentheses open parentheses 2 plus 4 close parentheses equals 3 open parentheses 0 close parentheses open parentheses 6 close parentheses equals 0. This means that 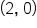open parentheses 2 comma space 0 close parentheses is a point on the graph, which is an x-intercept.

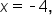
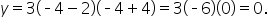When x equals short dash 4 comma y equals 3 open parentheses short dash 4 minus 2 close parentheses open parentheses short dash 4 plus 4 close parentheses equals 3 open parentheses short dash 6 close parentheses open parentheses 0 close parentheses equals 0. This means that 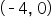open parentheses short dash 4 comma space 0 close parentheses is a point on the graph, which is also an x-intercept.

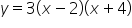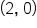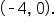
In conclusion, the graph of y equals 3 open parentheses x minus 2 close parentheses open parentheses x plus 4 close parentheses has x-intercepts at open parentheses 2 comma space 0 close parentheses and open parentheses short dash 4 comma space 0 close parentheses.

3. Parabolas

When quadratic equations are graphed, we call the curve a parabola. It has a distinct U shape to it (or an upside-down U shape if the parabola opens downward).

There is also either a minimum or a maximum point (also dependent upon which direction the parabola opens). This maximum or minimum point is known as the vertex of the parabola, and it lies on a line of symmetry to the graph. This means that one half of the parabola can be reflected about that line of symmetry to match up perfectly with the other half of the parabola.

EXAMPLE

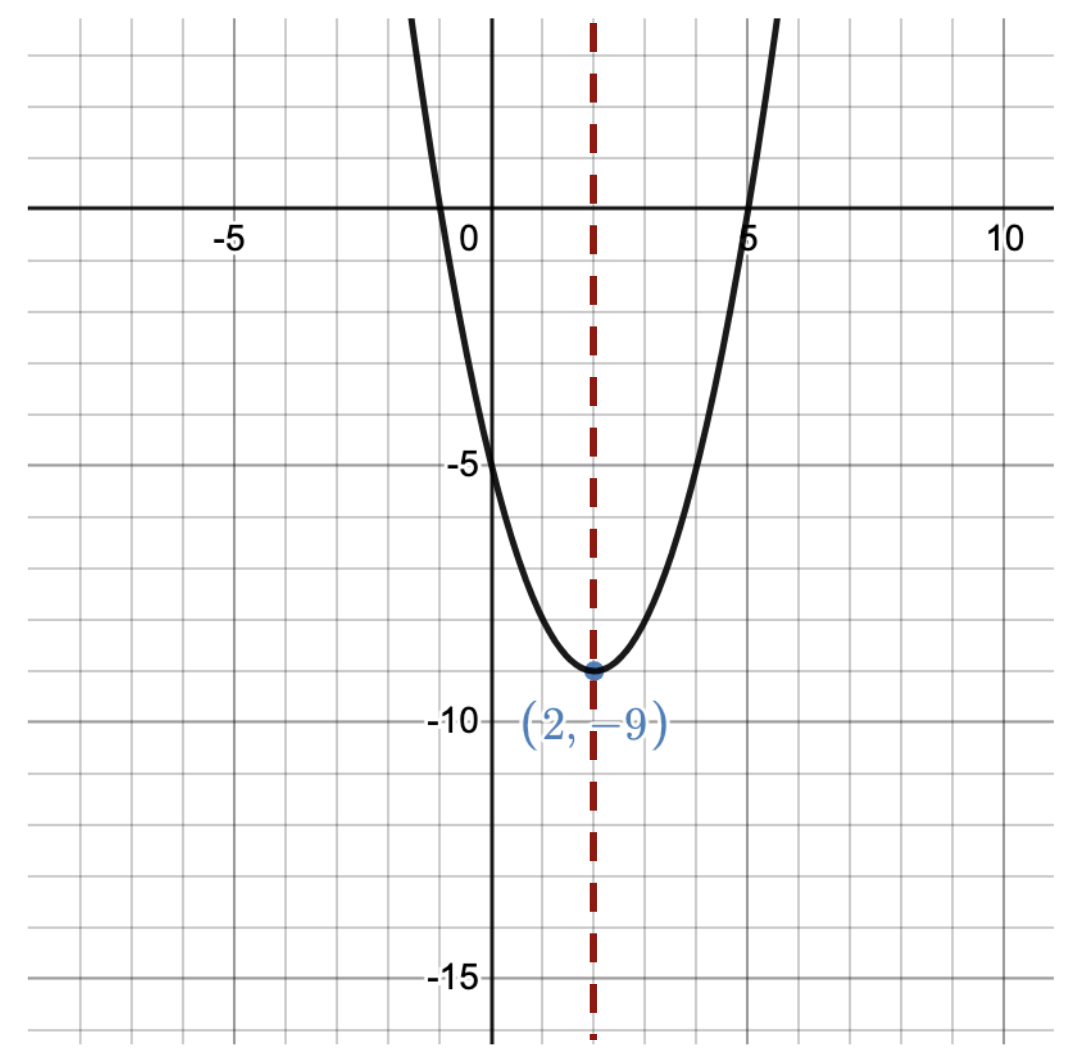
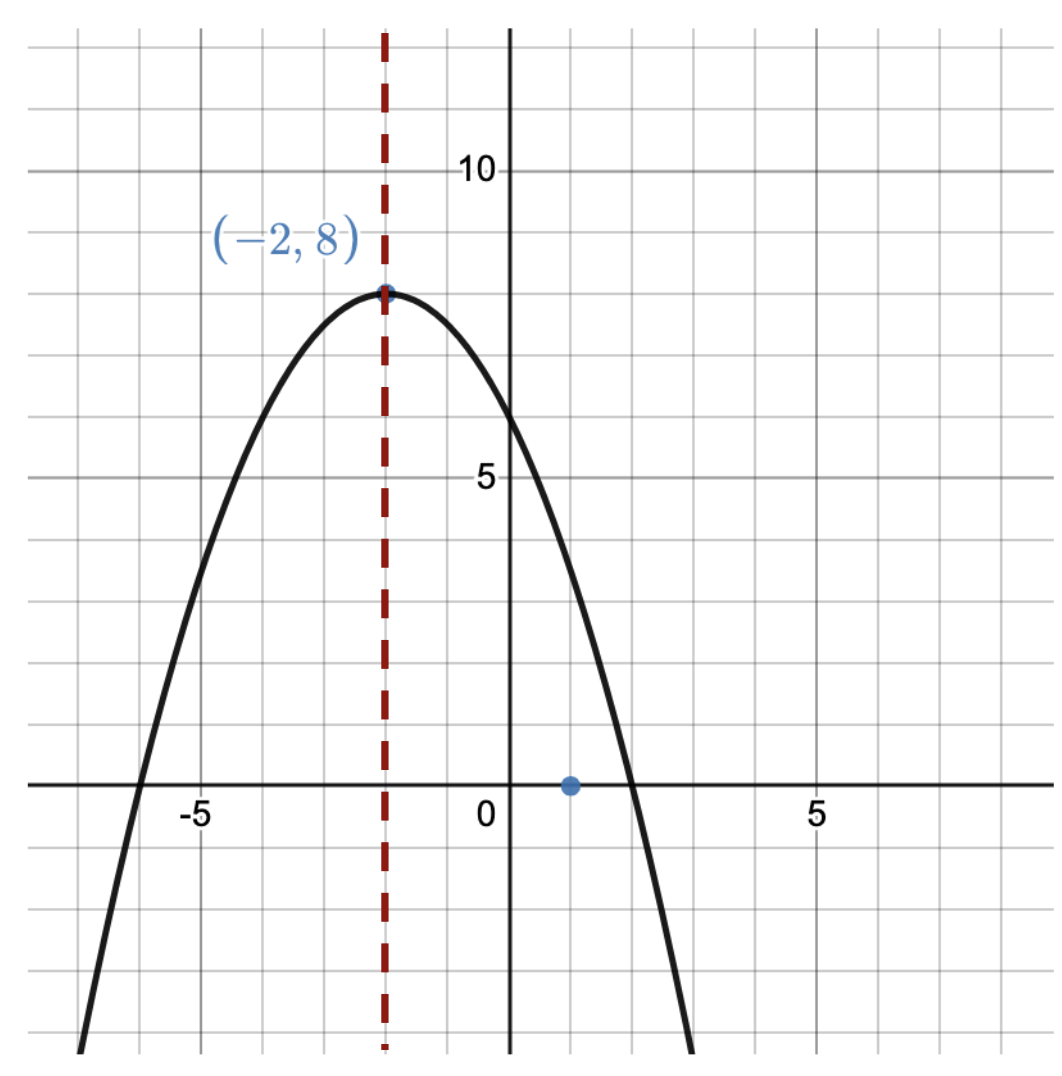
Here are a couple of graphs of parabolas. See if you can spot the vertex, and notice its symmetry:

U-Shape
Opens upward
Vertex: (2,-9) 		Upside-down U shape
Opens downward
Vertex: (-2,8)

hint
The leading coefficient to the equation (the value of "a" in each of the three forms listed in the section above) determines whether the parabola opens up or down. If a is positive, the parabola opens up (and has a U shape). If a is negative, the parabola opens down (and has an upside-down U shape). You'll learn more about this in a later lesson.

terms to know
Parabola
The shape of a quadratic equation on a graph; it is symmetric at the vertex.
Vertex (of a Parabola)
The maximum or minimum point of a parabola located on the axis of symmetry.

4. x-intercepts of Parabolas

An x-intercept of a quadratic equation is also referred to as a zero, or a root. This is because x-intercepts are x-values for which 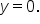y equals 0. Quadratic equations can have zero, one, or two real x-intercepts. There will never be three real x-intercepts to a quadratic equation. This is because parabolas can intersect the x-axis at most 2 times.

EXAMPLE

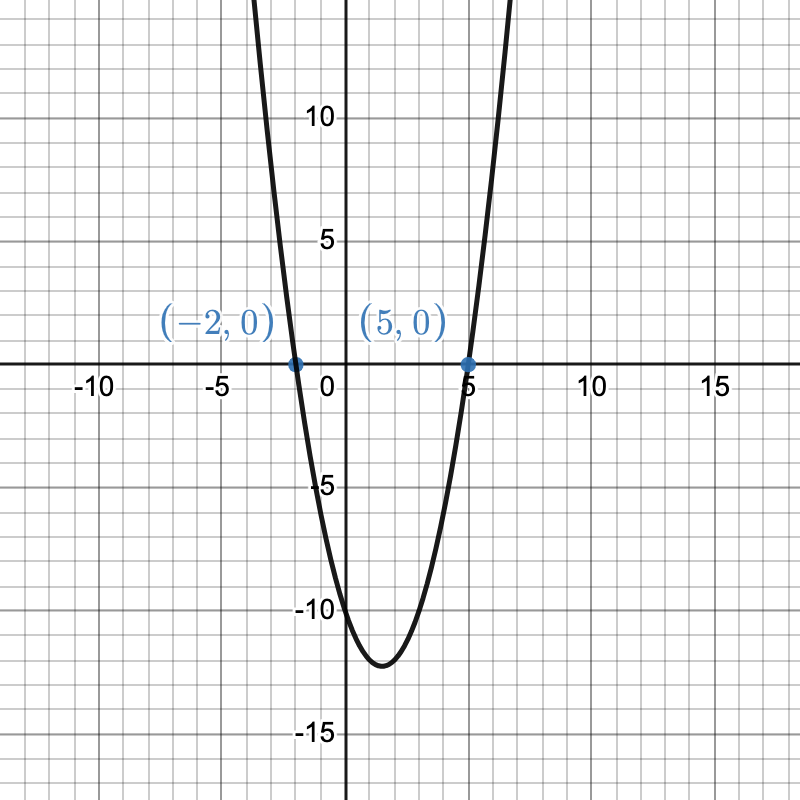
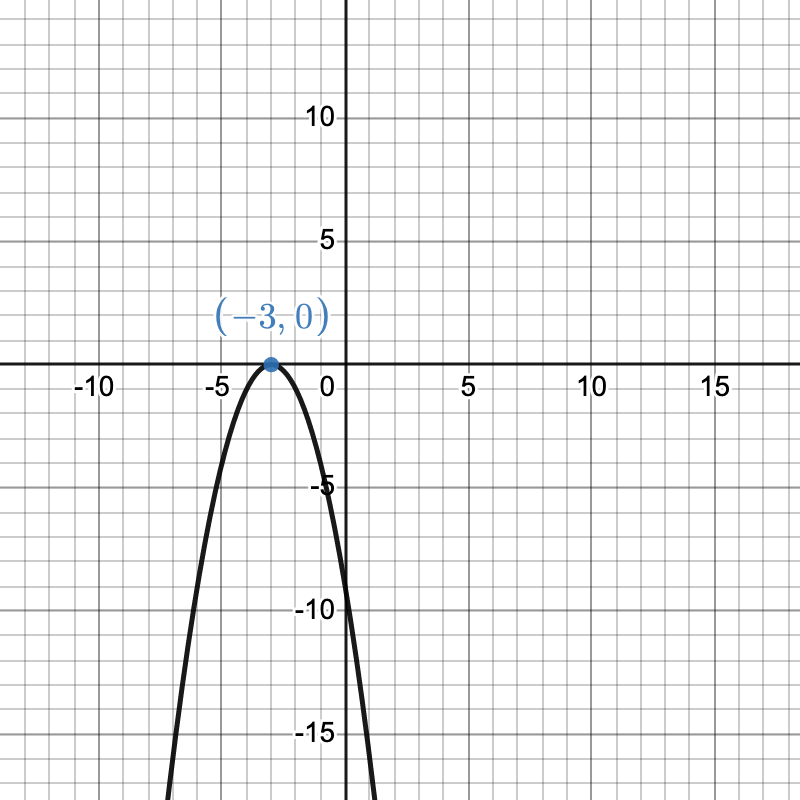
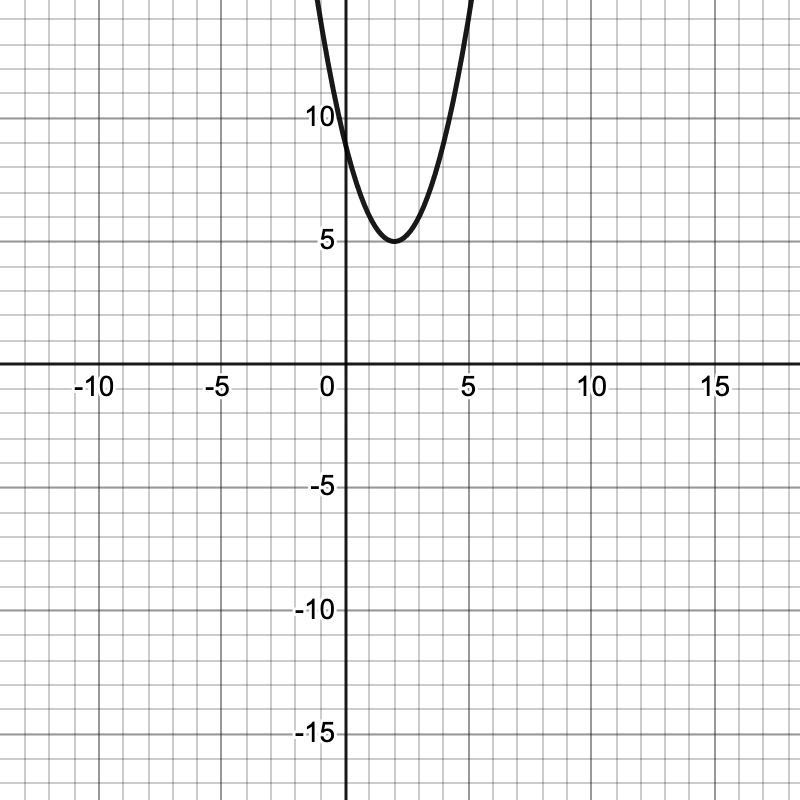
Take a look that the following graphs of parabolas and notice their solutions, or the spot where they intersect the x-axis.

Two Solutions One Solution No Solutions
Solutions: (-2,0) and (5,0) Solutions: (-3,0) No Real Solutions

summary
When we think of quadratics, we can think of quadratics as second degree polynomials. There are three different forms of quadratic equations: standard, vertex, and factored. The graph of a quadratic equation is called a parabola. Parabolas have either a minimum or a maximum point, which is called the vertex. The solutions to quadratic equations can also be called a root or a 0. The solution represents the x-intercepts of the parabola on a graph. And a quadratic equation can be solved algebraically by substituting 0 for y in the equation, and solving for x.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Parabola

The shape of a quadratic equation on a graph; it is symmetric at the vertex.

Quadratic

A second-degree polynomial, with an x-squared term as its highest degree term.

Vertex (of a Parabola)

The maximum or minimum point of a parabola located on the axis of symmetry.

Formulas to Know
Factored Form of a Quadratic Equation

y equals a left parenthesis x minus x subscript 1 right parenthesis left parenthesis x minus x subscript 2 right parenthesis

Quadratic Formula

x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

Standard Form of a Quadratic Equation

y equals a x squared plus b x plus c

Vertex Form of a Quadratic Equation

y equals a open parentheses x minus h close parentheses squared plus k

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.