Introduction to Logarithms

1. Introduction to Logarithms

When solving for any type of equation, a sound strategy is to apply inverse operations to undo operations being performed to the variable. Doing so isolates the variable to one side of the equation, where we can then evaluate the other side to find our solution. For example, multiplication and division are inverse operations, and addition and subtraction are inverse operations.

In general, exponential equations can be solved by applying a logarithm to both sides of the equation. This is because logarithms and exponents are inverse operations.

term to know

Logarithm

The inverse of a power, the logarithm describes how many times a number should be multiplied by itself to result in another number.

2. Relating Logarithms to Exponential Equations

There is an inverse relationship between logarithms and exponents. For example, if we have the expression 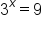, we can gather that x equals 2, because 3 squared equals 9 ().

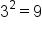As a logarithmic expression, we can write this equivalently as 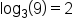. This reads, "the log, base 3, of 9 is 2." The expression tells us that the base number, 3, must be raised to the power of 2 in order to equal 9.

In general, we can write the relationship between logarithms and exponents as follows:

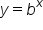
	Exponential equation
	Logarithmic equation

Notice that x and y switched as being isolated onto one side of the equals sign. This is characteristic of inverse relationships. Also note that the base to the exponential is the base of the logarithm.

formula to know

Logarithmic Form to Exponential Form

Let's use this relationship to rewrite the exponential equation as a logarithmic equation:

Exponential Form	Logarithmic Form

3. Common Log and Natural Log

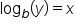
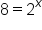
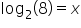
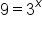
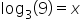
If you have a scientific calculator that can compute logarithms, there are likely two kinds of log buttons on your calculator: one that simply says "log" and another that says "ln." The first button, "log," is known as common log, while the other, "ln," is referred to as the natural log.

They are both logarithms, but their difference is in their base. Common log operates under a base of 10. So if you ever see expressions such as log(42) or log(67), the base of the log is 10. This means that we can rewrite each expression as 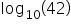or 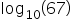. The log with base 10 is common, so we assume the base is 10 if it is not written.

hint

Whenever a base is not explicitly written next to "log," it is assumed to be the common log, which is base 10.

The abbreviation "ln" comes from the Latin logarithmus naturali. The base of this logarithm is the mathematical constant "e". The constant "e", or Euler's constant, is approximately equal to 2.718282. If you have the natural log button (ln) on your calculator, definitely use it for the most accurate calculations. Otherwise, use the approximation 2.718282.

hint

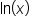Natural log, or ln, operates in base e, which is approximately equal to 2.718282. Note, and 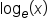are the same expressions.

4. Evaluating Logarithmic Expressions

We can use the relationship between exponential equations and logarithmic equations to evaluate expressions by thinking about how many times we must multiply a given number by itself to result in another given number.

EXAMPLE

Evaluate .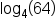

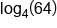
	The logarithmic expression.
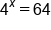
	Rewrite using exponents.
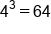
	4 cubed, or 4 raised to the third power, results in 64.
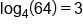
	3 is the solution to .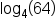

EXAMPLE

Evaluate .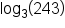

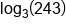
	The logarithmic expression.
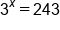
	Rewrite using exponents.
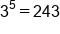
	3 raised to the 5th power is 243.
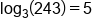
	5 is the solution to .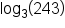

In the example above, notice how the bases are the same in both exponential and logarithmic form.

try it

Consider the equation .

Evaluate this equation.

	The logarithmic expression.
	Rewrite using exponents.
	2 raised to the 7th power is 128.
	7 is the solution to

summary

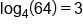
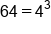
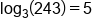
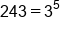
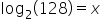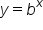In this lesson, you covered an introduction to logarithms, understanding that there is an inverse relationship between logarithms and exponents. In an exponential equation, a base number is raised to a variable power and represented as . Relating logarithms to exponents, the input of the logarithmic function is the output of the exponential function, and the output of the logarithmic function is the input of the exponential function. You learned that there are two types of log, common log and natural log. The common log is a logarithm with a base of 10. An expression with no base explicitly written next to "log," like log(42), implies a base of 10. The natural log is a logarithm with a base e, where e is approximately equal to 2.718281. You learned that when evaluating logarithmic expressions, you can rewrite them using exponents.

Best of luck in your learning!