Table of Contents |
It should go without saying that the main difference between a system of inequalities and a system of equations is that a system of inequalities consists of at least two inequalities, rather than two equations.
As we will discuss below, there is also a major difference in how we interpret the solutions to a system of inequalities. However, one thing remains the same: the variables within the inequalities of the system must have matching definitions. Otherwise, we cannot consider the relationship to be a system. This becomes important when working with systems of inequalities in a situational context.
EXAMPLE
If x represents apples in one inequality, it must represent apples in all of the inequalities in the system.Just as a solution to a system of equations satisfies all equations in the system, solutions to a system of inequalities must satisfy all inequalities in the system. Sometimes, a coordinate pair (x, y) will satisfy one or two of the inequalities in the system, but not all. In these cases, the coordinate pair does not represent a solution to the entire system. One way to think about inequalities is that they represent boundaries. In a system, there are several boundaries, each of which is represented by an inequality. In this sense, a solution to a system of inequalities fits with every boundary defined by the inequalities.
Let's take a visual approach to understand solutions to a system of inequalities.
EXAMPLE
Below is a graph of the following system: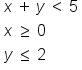
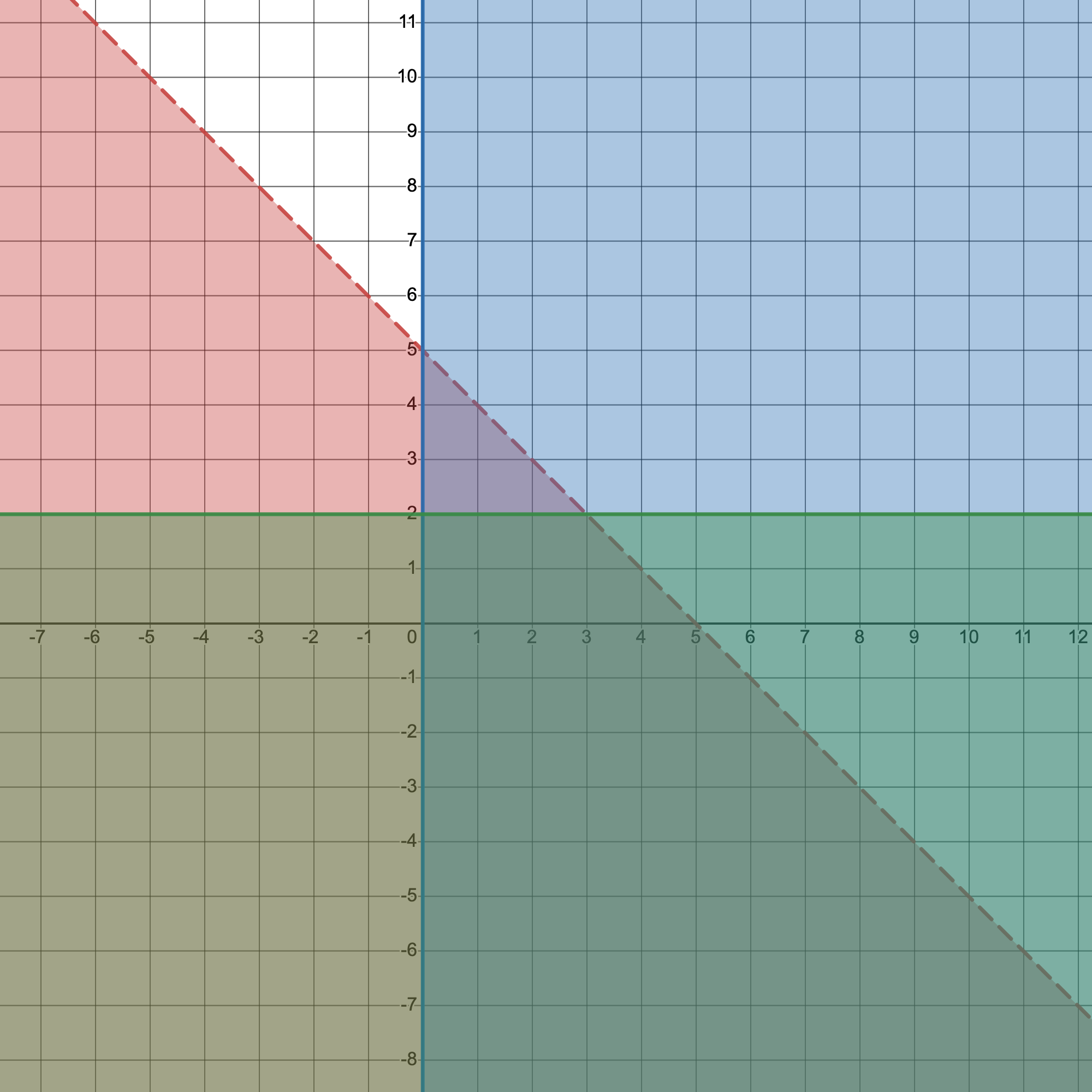
| Point | Solution? | Explanation |
|---|---|---|
| (2, 1) | Yes | (2, 1) is within the shaded region. |
| (-2, 2) | No | Although (-2, 2) lies on the green line, it is outside the shaded region. |
| (0, 5) | No | Although (0, 5) lies on both the red and blue line, it is outside the shaded region. |
| (6, -4) | Yes | (6, -4) is within the shaded region. |
| (8, 6) | No | (8, 6) is outside the shaded region. |
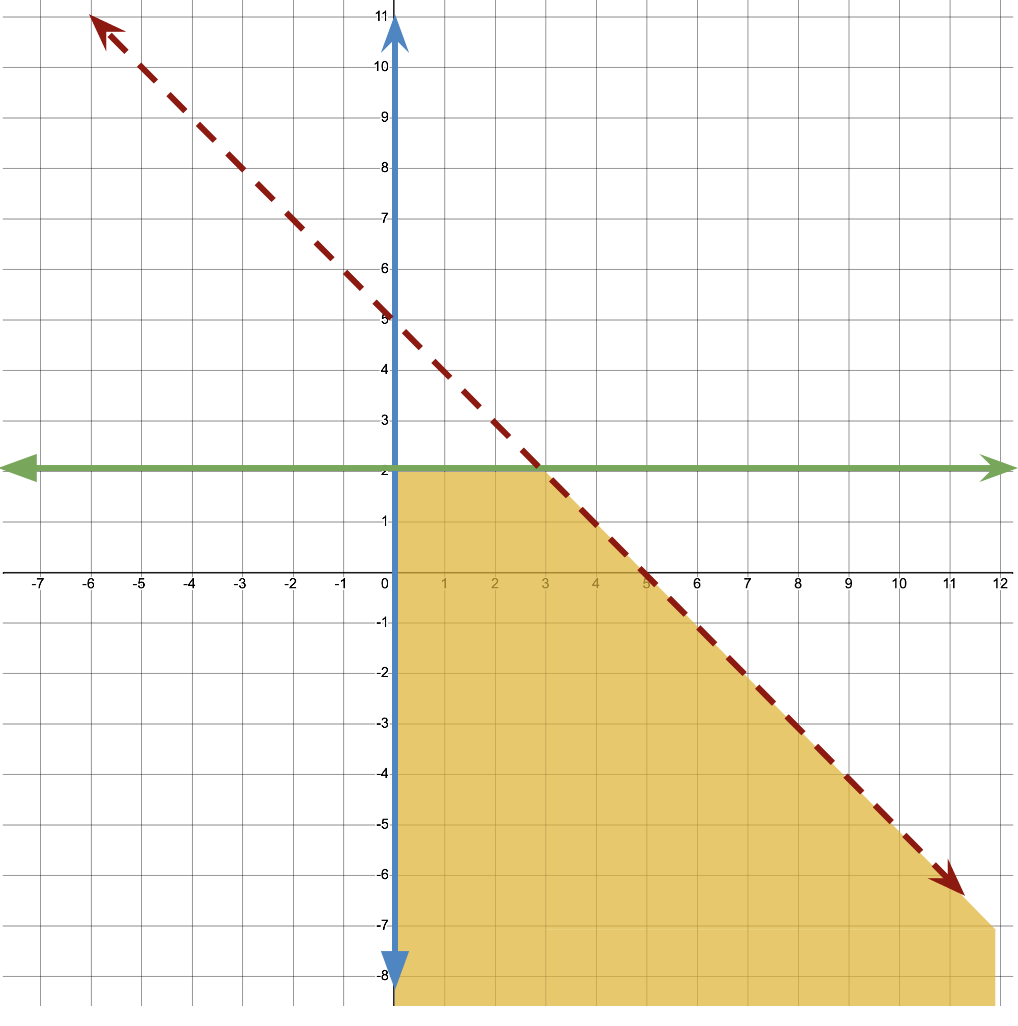
Sometimes a graph of a system will have overlapping solution regions to individual inequalities in the system, without an overlap of solutions to all inequalities. Recall that solutions to the entire system must fit within all boundaries defined by the system. Thus, when no overlap between all inequalities exist, there is no solution to the system, although we may be tempted to think there are, because some overlaps exist.
EXAMPLE
Below is a graph of the following system: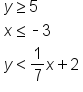
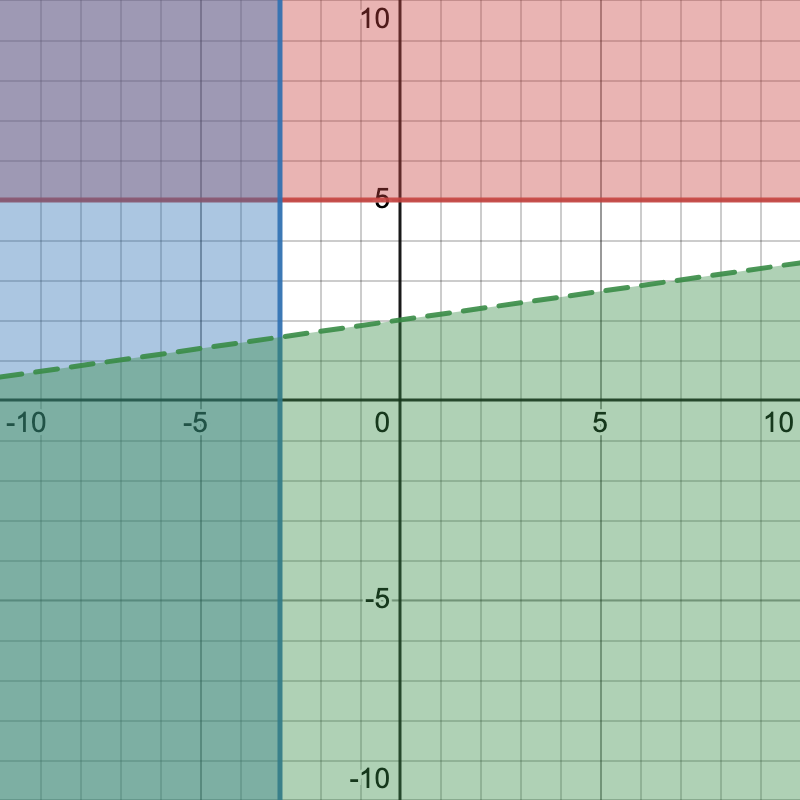
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License