Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Intercepts of Quadratic Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will apply properties of quadratic equations to find x- and y-intercepts of the graph of a quadratic function. Specifically, this lesson will cover:

Table of Contents

1. Finding the x- and y-Intercepts of a Quadratic Function

Consider a quadratic function in the form 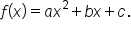f open parentheses x close parentheses equals a x squared plus b x plus c. Given that 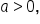a greater than 0 comma consider these graphs:

No x-Intercept One x-Intercept Two x-Intercepts

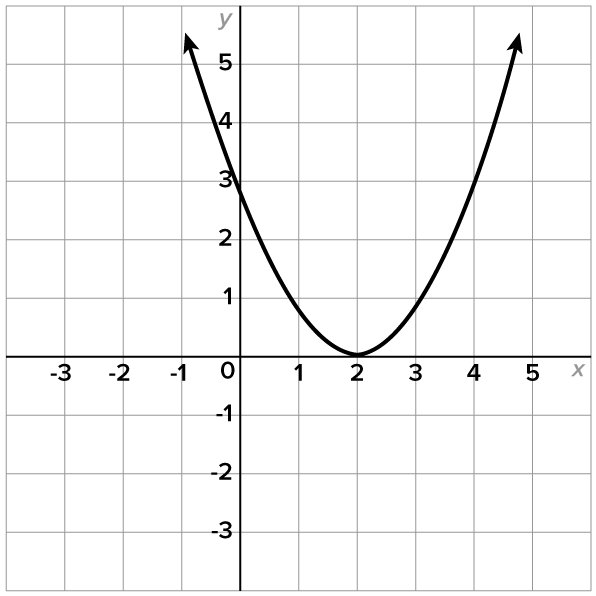
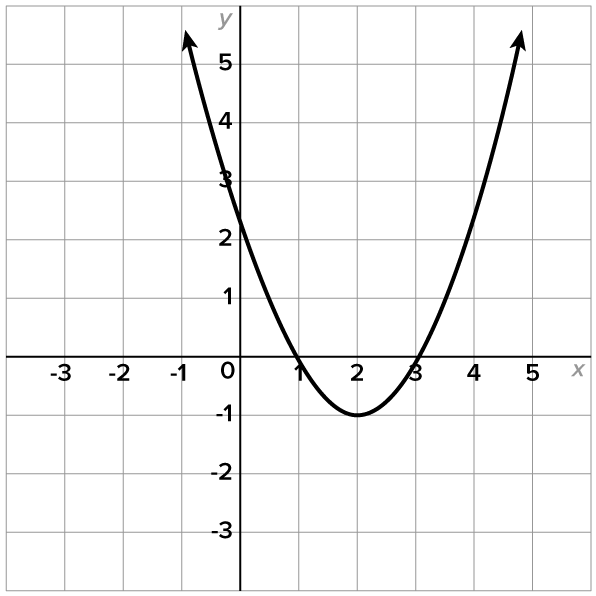
Based on these graphs, the graph of a quadratic function can have zero, one, or two x-intercepts. Also, note that each graph contains one y-intercept. This is true for every quadratic function.

Given a function 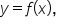y equals f open parentheses x close parentheses comma recall:

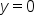  • To find the x-intercept(s) of the graph, let y equals 0 and solve for x.
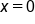  • To find the y-intercept of the graph, let x equals 0 and solve for y.
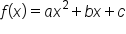This means that every quadratic function f open parentheses x close parentheses equals a x squared plus b x plus c has a y-intercept at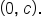 open parentheses 0 comma space c close parentheses.

Finding the x-intercepts is a bit more complicated since this will involving solving 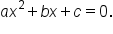a x squared plus b x plus c equals 0.

EXAMPLE

Find all x- and y-intercepts of the graph of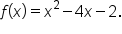 f open parentheses x close parentheses equals x squared minus 4 x minus 2.

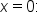
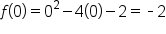
The y-intercept is the point that corresponds to x equals 0 colon f open parentheses 0 close parentheses equals 0 squared minus 4 open parentheses 0 close parentheses minus 2 equals short dash 2

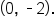
Therefore, the y-intercept is open parentheses 0 comma space short dash 2 close parentheses.

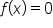The x-intercept(s) are found by setting f open parentheses x close parentheses equals 0 and solving for x.

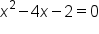
x squared minus 4 x minus 2 equals 0 This is the original equation.
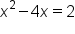
x squared minus 4 x equals 2 Add 2 to both sides (preparing to complete the square).
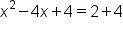
x squared minus 4 x plus 4 equals 2 plus 4 Add 4 to both sides.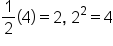
1 half open parentheses 4 close parentheses equals 2 comma space 2 squared equals 4
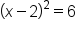
open parentheses x minus 2 close parentheses squared equals 6 Write the left side as a quantity squared, and simplify the right side.
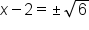
x minus 2 equals plus-or-minus square root of 6 Apply the square root principle.
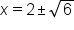
x equals 2 plus-or-minus square root of 6 Add 2 to both sides.

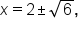Since the solutions are x equals 2 plus-or-minus square root of 6 comma this means that the graph of f open parentheses x close parentheses has two x-intercepts: 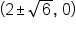open parentheses 2 plus-or-minus square root of 6 comma space 0 close parentheses

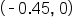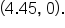
These can be approximated to open parentheses short dash 0.45 comma space 0 close parentheses and open parentheses 4.45 comma space 0 close parentheses.

These points can be seen on the graph that is pictured here.

EXAMPLE

Find all x- and y-intercepts of the graph of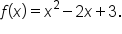 f open parentheses x close parentheses equals x squared minus 2 x plus 3.

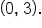
Note that the constant term is 3. Then, the y-intercept is open parentheses 0 comma space 3 close parentheses.

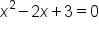To find the x-intercept(s), set x squared minus 2 x plus 3 equals 0 and solve. This time we will use the quadratic formula.

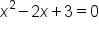
x squared minus 2 x plus 3 equals 0 This is the original equation.
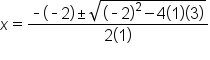
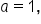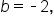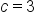x equals fraction numerator short dash open parentheses short dash 2 close parentheses plus-or-minus square root of open parentheses short dash 2 close parentheses squared minus 4 open parentheses 1 close parentheses open parentheses 3 close parentheses end root over denominator 2 open parentheses 1 close parentheses end fraction Substitute a equals 1 comma b equals short dash 2 comma and c equals 3 into the quadratic formula.
x equals fraction numerator 2 plus-or-minus square root of short dash 8 end root over denominator 2 end fraction Simplify.

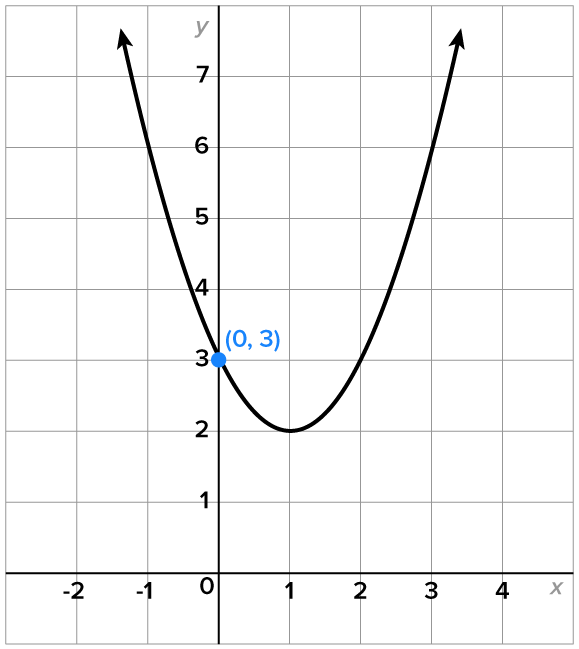
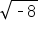At this point, we can stop. Since square root of short dash 8 end root is not a real number, it follows that the solutions to the equation are not real. Thus, the graph of f open parentheses x close parentheses has no x-intercepts.

The graph of f open parentheses x close parentheses is shown below.

watch
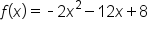We will find all x- and y-intercepts of the function f open parentheses x close parentheses equals short dash 2 x squared minus 12 x plus 8 in this video.

try it
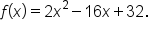
Consider the function f open parentheses x close parentheses equals 2 x squared minus 16 x plus 32.
Find all x- and y-intercepts.
The y-intercept is open parentheses 0 comma space f open parentheses 0 close parentheses close parentheses.

With f open parentheses 0 close parentheses equals 2 open parentheses 0 close parentheses squared minus 16 open parentheses 0 close parentheses plus 32 equals 32 comma the y-intercept is open parentheses 0 comma space 32 close parentheses.

The x-intercepts are found by setting f open parentheses x close parentheses equals 0 and solving for x.

2 x squared minus 16 x plus 32 equals 0 Set f open parentheses x close parentheses equals 0.
2 open parentheses x squared minus 8 x plus 16 close parentheses equals 0 Remove common factor of 2.
2 open parentheses x minus 4 close parentheses open parentheses x minus 4 close parentheses equals 0 Factor the trinomial.
x equals 4 Set each factor equal to 0. Since 2 cannot equal 0 and x minus 4 is a factor twice, the only solution is when x minus 4 equals 0 comma which means x equals 4.

This means that the graph of f open parentheses x close parentheses has one x-intercept, which is at open parentheses 4 comma space 0 close parentheses.

2. Applications of Intercepts of Quadratic Functions

In applications that are modeled by quadratic functions, intercepts give important information.

EXAMPLE

A rock is thrown upward from the top of a 112-foot cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height (in feet) above the ocean after t seconds is modeled by the equation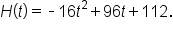 H open parentheses t close parentheses equals short dash 16 t squared plus 96 t plus 112.

Question #1: What is the initial height of the object?

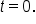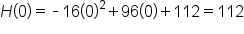This occurs when t equals 0. Then, H open parentheses 0 close parentheses equals short dash 16 open parentheses 0 close parentheses squared plus 96 open parentheses 0 close parentheses plus 112 equals 112 feet. This means that the point 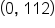open parentheses 0 comma space 112 close parentheses is on the graph, which is a y-intercept.

Question #2: At what time(s) does the object strike the ground?

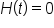Set H open parentheses t close parentheses equals 0 and solve for t.

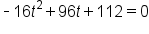
short dash 16 t squared plus 96 t plus 112 equals 0 This is the original equation.
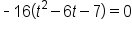
short dash 16 open parentheses t squared minus 6 t minus 7 close parentheses equals 0 Factor out -16.
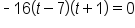
short dash 16 open parentheses t minus 7 close parentheses open parentheses t plus 1 close parentheses equals 0 Factor the quadratic.
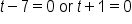
t minus 7 equals 0 space or space t plus 1 equals 0 Set each variable factor equal to 0.
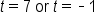
t equals 7 space or space t equals short dash 1 Solve each equation.

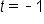Thus, the object strikes the ocean after 7 seconds. The solution t equals short dash 1 does not make sense in this particular problem since t is the number of seconds after the object was thrown. Negative values of time are not considered.

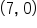This means that the point open parentheses 7 comma space 0 close parentheses is also on the graph of 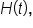H open parentheses t close parentheses comma and is a t-intercept (in place of an x-intercept).

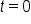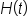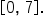
Since the object is thrown at t equals 0 and strikes the ocean after 7 seconds, the domain of H open parentheses t close parentheses is open square brackets 0 comma space 7 close square brackets.

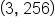Note: as well as intercepts, recall that the vertex also gives us valuable information. Using the vertex formula that we learned in a previous lesson, we find that the point open parentheses 3 comma space 256 close parentheses is the vertex. Since the coefficient of 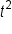t squared is negative, we know that a maximum occurs at the vertex. In this situation, this means that after 3 seconds, the maximum height of 256 feet is achieved.

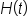The graph of H open parentheses t close parentheses is shown below.

try it
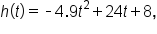A ball is thrown from the top of the building. Its height, in meters above the ground, is given by the function h open parentheses t close parentheses equals short dash 4.9 t squared plus 24 t plus 8 comma where t is the time in seconds since the ball was thrown.
What is the y-intercept of the graph of h, and what does it represent in this situation?
The y-intercept is open parentheses 0 comma space 8 close parentheses. It means that the ball was thrown from a height of 8 meters above the ground. It also means that the building is 8 meters tall.
Find all t-intercepts of the graph of h. What do they represent in this situation? Round to the nearest hundredth when needed.
To find the t-intercepts, set h open parentheses t close parentheses equals 0 and solve for t.

short dash 4.9 t squared plus 24 t plus 8 equals 0 Set h open parentheses t close parentheses equals 0.
t equals fraction numerator short dash 24 plus-or-minus square root of open parentheses 24 close parentheses squared minus 4 open parentheses short dash 4.9 close parentheses open parentheses 8 close parentheses end root over denominator 2 open parentheses short dash 4.9 close parentheses end fraction Use the quadratic formula with a equals short dash 4.9 comma b equals 24 comma and c equals 8.
t equals fraction numerator short dash 24 plus-or-minus square root of 732.8 end root over denominator short dash 9.8 end fraction Simplify under the radical and the other terms as well.
t equals fraction numerator short dash 24 plus square root of 732.8 end root over denominator short dash 9.8 end fraction almost equal to short dash 0.31
t equals fraction numerator short dash 24 minus square root of 732.8 end root over denominator short dash 9.8 end fraction almost equal to 5.21 		Approximate each solution.

Thus, the t-intercepts are open parentheses 5.21 comma space 0 close parentheses and open parentheses short dash 0.31 comma space 0 close parentheses. The positive intercept tells us that it takes 5.21 seconds for the ball to strike the ground. The negative intercept has no meaning in this situation.

summary
In this lesson, you learned that the graph of any quadratic function contains one y-intercept, while it may have one, two, or no x-intercepts. You can find the y-intercept of a quadratic function by letting x equals 0 and solving for y, but finding the x-intercept is slightly more complicated and requires using the methods of solving quadratic equations from the last tutorial. You also learned that in real-world applications involving quadratic functions, such as a situation involving an object being launched, the intercepts provide important information about the initial height of the object and the time it takes for the object to strike a surface.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.