Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Instantaneous Rate of Change

Author: Sophia
PDF Version

what's covered
In this lesson, you will compute and visualize the instantaneous rate of change of a function. Specifically, this lesson will cover:

Table of Contents

1. Instantaneous Rate of Change

In the last section, we computed average rates of change, which require an interval of time. What if we want to compute the instantaneous rate of change, which is the rate of change at one specific point?

Let’s say a tennis ball is dropped off the top of a building. Its height after t seconds is described by the function y open parentheses t close parentheses equals short dash 16 t squared plus 120. Suppose we want to find the instantaneous rate of change at the instant that 2 seconds have passed.

To see if we can find a pattern, let’s find average rates of change on small intervals of time starting with 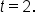t equals 2.

Interval Length of Interval Average Rate of Change
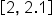
open square brackets 2 comma space 2.1 close square brackets 0.1 seconds fraction numerator y open parentheses 2.1 close parentheses minus y open parentheses 2 close parentheses over denominator 2.1 minus 2 end fraction equals fraction numerator 49.44 minus 56 over denominator 0.1 end fraction equals short dash 65.6 ft/sec
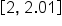
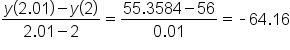open square brackets 2 comma space 2.01 close square brackets 0.01 seconds fraction numerator y open parentheses 2.01 close parentheses minus y open parentheses 2 close parentheses over denominator 2.01 minus 2 end fraction equals fraction numerator 55.3584 minus 56 over denominator 0.01 end fraction equals short dash 64.16 ft/sec
open square brackets 2 comma space 2.001 close square brackets 0.001 seconds 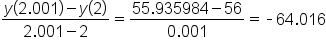fraction numerator y open parentheses 2.001 close parentheses minus y open parentheses 2 close parentheses over denominator 2.001 minus 2 end fraction equals fraction numerator 55.935984 minus 56 over denominator 0.001 end fraction equals short dash 64.016 ft/sec

Notice that as the length of the interval decreases, the average rate of change seems to be approaching a value. It is safe to estimate the instantaneous rate of change as -64 ft per second (we will see later that this is the actual answer).

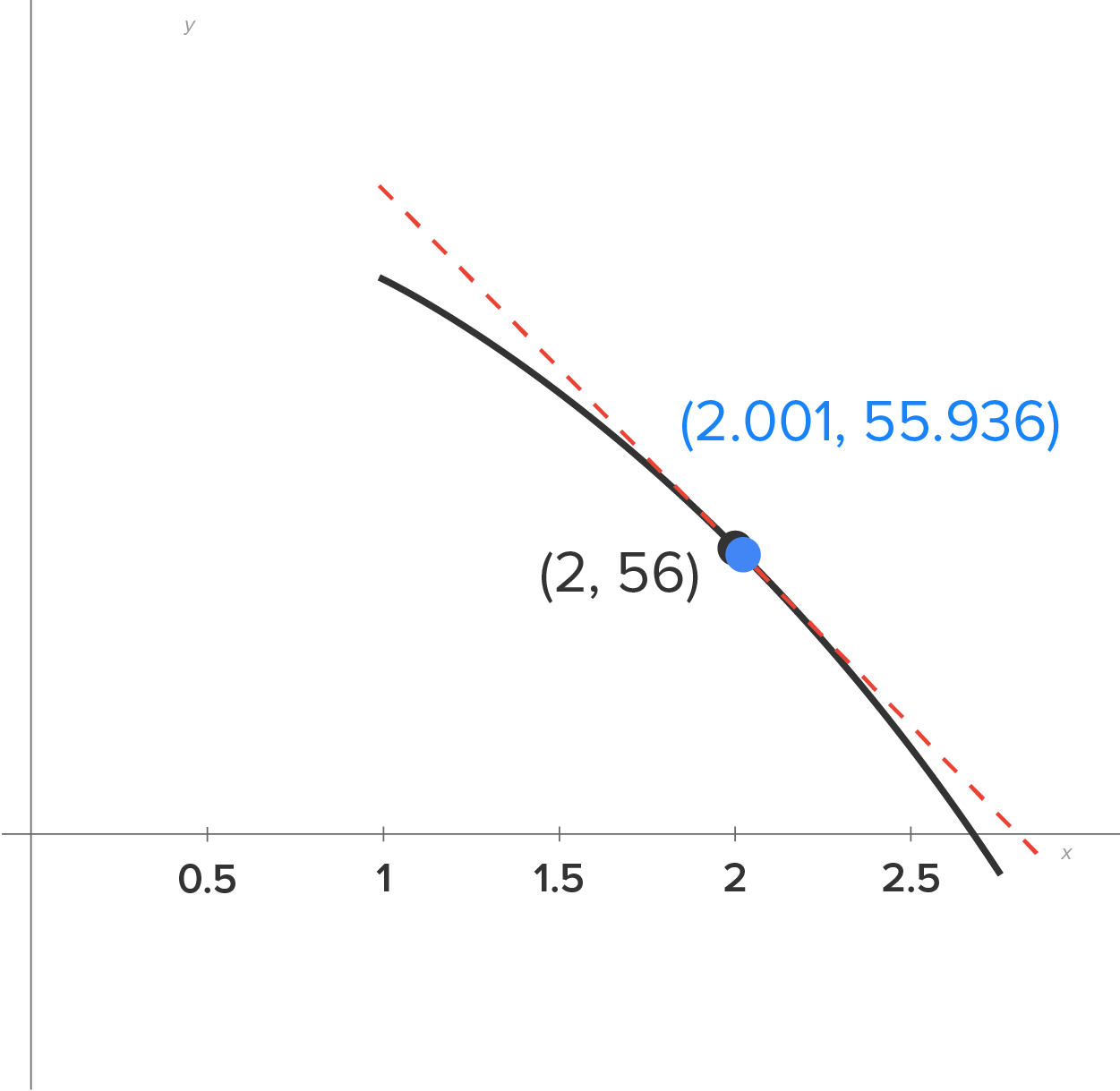
A graph with an x-axis and y-axis, where the x-axis ranges from 0 to 2.5. A downward-sloping curve extends in the first quadrant, passing through a marked point at (2, 56). A dashed line slants downward in the first quadrant, passing through a marked point at (2.001, 55.936).

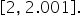Let’s examine the curve y open parentheses t close parentheses equals short dash 16 t squared plus 120 and the secant line for the interval open square brackets 2 comma space 2.001 close square brackets. (The curve is solid; the secant line is dashed).

Notice that the two points are nearly indistinguishable.

Furthermore, the secant line appears to only pass through one point instead of two (remember, because they are so close together), so the secant line actually looks like a tangent line!

big idea
The instantaneous rate of change of a function is represented graphically by the slope of the tangent line.

term to know
Instantaneous Rate of Change
The rate of change of a function at a specific point.

2. Computing Instantaneous Rate of Change

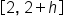The problem we just completed in the previous section can be generalized by finding the average rate of change in y open parentheses t close parentheses equals short dash 16 t squared plus 120 over the interval open square brackets 2 comma space 2 plus h close square brackets for small values of h.

Since the instantaneous rate of change is the result of letting h get smaller and smaller, here is our plan to find the instantaneous rate of change for y open parentheses t close parentheses colon

step by step
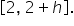
  1. Calculate the average rate of change on the interval open square brackets 2 comma space 2 plus h close square brackets.
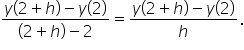
    The expression for the average rate of change is fraction numerator y open parentheses 2 plus h close parentheses minus y open parentheses 2 close parentheses over denominator open parentheses 2 plus h close parentheses minus 2 end fraction equals fraction numerator y open parentheses 2 plus h close parentheses minus y open parentheses 2 close parentheses over denominator h end fraction.
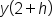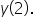
    First, find y open parentheses 2 plus h close parentheses and y open parentheses 2 close parentheses.

    table attributes columnalign left end attributes row cell y open parentheses 2 plus h close parentheses equals short dash 16 open parentheses 2 plus h close parentheses squared plus 120 end cell row cell equals short dash 16 open parentheses 4 plus 4 h plus h squared close parentheses plus 120 end cell row cell equals short dash 64 minus 64 h minus 16 h squared plus 120 end cell row cell equals 56 minus 64 h minus 16 h squared end cell end table

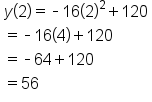
    table attributes columnalign left end attributes row cell y open parentheses 2 close parentheses equals short dash 16 open parentheses 2 close parentheses squared plus 120 end cell row cell equals short dash 16 open parentheses 4 close parentheses plus 120 end cell row cell equals short dash 64 plus 120 end cell row cell equals 56 end cell end table
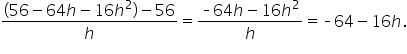
    Then, the average rate of change is fraction numerator open parentheses 56 minus 64 h minus 16 h squared close parentheses minus 56 over denominator h end fraction equals fraction numerator short dash 64 h minus 16 h squared over denominator h end fraction equals short dash 64 minus 16 h.
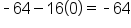  2. The instantaneous rate of change is the average rate of change as the value of h gets smaller and smaller. In the simplified expression, substitute h equals 0. This gives short dash 64 minus 16 open parentheses 0 close parentheses equals short dash 64 ft/sec.

    Conclusion: the instantaneous rate of change is -64 ft/sec.

big idea
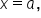To find the instantaneous rate of change of f open parentheses x close parentheses at x equals a comma follow these steps.
  1. Find and simplify fraction numerator f open parentheses a plus h close parentheses minus f open parentheses a close parentheses over denominator h end fraction.
    Note, this should look familiar…it looks like a difference quotient!
  2. Once simplified, substitute h equals 0 to get the instantaneous rate of change.

EXAMPLE

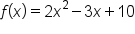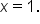Compute the instantaneous rate of change of f open parentheses x close parentheses equals 2 x squared minus 3 x plus 10 when x equals 1. We know the average rate of change is fraction numerator f open parentheses 1 plus h close parentheses minus f open parentheses 1 close parentheses over denominator h end fraction.

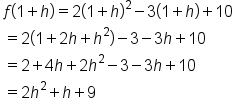
table attributes columnalign left end attributes row cell f open parentheses 1 plus h close parentheses equals 2 open parentheses 1 plus h close parentheses squared minus 3 open parentheses 1 plus h close parentheses plus 10 end cell row cell equals 2 open parentheses 1 plus 2 h plus h squared close parentheses minus 3 minus 3 h plus 10 end cell row cell equals 2 plus 4 h plus 2 h squared minus 3 minus 3 h plus 10 end cell row cell equals 2 h squared plus h plus 9 end cell end table

table attributes columnalign left end attributes row cell f open parentheses 1 close parentheses equals 2 open parentheses 1 close parentheses squared minus 3 open parentheses 1 close parentheses plus 10 end cell row cell equals 2 minus 3 plus 10 end cell row cell equals 9 end cell end table

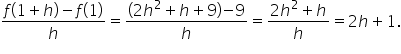Then, fraction numerator f open parentheses 1 plus h close parentheses minus f open parentheses 1 close parentheses over denominator h end fraction equals fraction numerator open parentheses 2 h squared plus h plus 9 close parentheses begin display style minus end style begin display style 9 end style over denominator h end fraction equals fraction numerator 2 h squared plus h over denominator h end fraction equals 2 h plus 1. 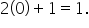The instantaneous rate of change is 2 open parentheses 0 close parentheses plus 1 equals 1.

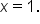
Reminder: This is also the slope of the tangent line when x equals 1.

try it
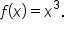
Consider the function f open parentheses x close parentheses equals x cubed.
Find the instantaneous rate of change of the function when x = 4.
First, find f open parentheses 4 plus h close parentheses and f open parentheses 4 close parentheses.

table attributes columnalign left end attributes row cell f open parentheses 4 plus h close parentheses equals open parentheses 4 plus h close parentheses cubed end cell row cell equals open parentheses 4 plus h close parentheses open parentheses 4 plus h close parentheses open parentheses 4 plus h close parentheses end cell row cell equals open parentheses 16 plus 8 h plus h squared close parentheses open parentheses 4 plus h close parentheses end cell row cell equals h cubed plus 12 h squared plus 48 h plus 64 end cell end table

table attributes columnalign left end attributes row cell f open parentheses 4 close parentheses equals 4 cubed end cell row cell equals 64 end cell end table

Then, fraction numerator f open parentheses 4 plus h close parentheses minus f open parentheses 4 close parentheses over denominator h end fraction equals fraction numerator open parentheses h cubed plus 12 h squared plus 48 h plus 64 close parentheses begin display style minus end style begin display style 64 end style over denominator h end fraction equals fraction numerator h cubed plus 12 h squared plus 48 h over denominator h end fraction equals h squared plus 12 h plus 48.

The instantaneous rate of change is 0 squared plus 12 open parentheses 0 close parentheses plus 48 equals 48.

watch
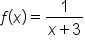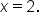
The following video walks you through the process of calculating the instantaneous rate of change of f open parentheses x close parentheses equals fraction numerator 1 over denominator x plus 3 end fraction when x equals 2.

summary
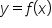In this lesson, you learned that the instantaneous rate of change of a function gives the rate of change of the function at a single point (as opposed to average rate of change, which requires two points). The geometric interpretation of instantaneous rate of change is that it is the slope of the line tangent to y equals f open parentheses x close parentheses at that specific point. You also learned how to compute the instantaneous rate of change, which enables you to calculate instantaneous velocity at a specific point in time.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 1 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Instantaneous Rate of Change

The rate of change of a function at a specific point.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.