Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Inflection Points

Author: Sophia
PDF Version

what's covered
In this tutorial, we will find inflection points that occur when a curve changes concavity. Inflection points are useful in modeling an epidemic. Specifically, this lesson will cover:

Table of Contents

1. Defining the Point of Inflection

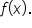
In the last tutorial, we learned that f apostrophe apostrophe open parentheses x close parentheses gives information about the concavity of f open parentheses x close parentheses.

When a curve has a point where it transitions between being concave up and concave down, and the tangent line exists, the point is called an inflection point (or point of inflection).

Consider the graph shown below, which represents the number of people who have become infected with a disease.

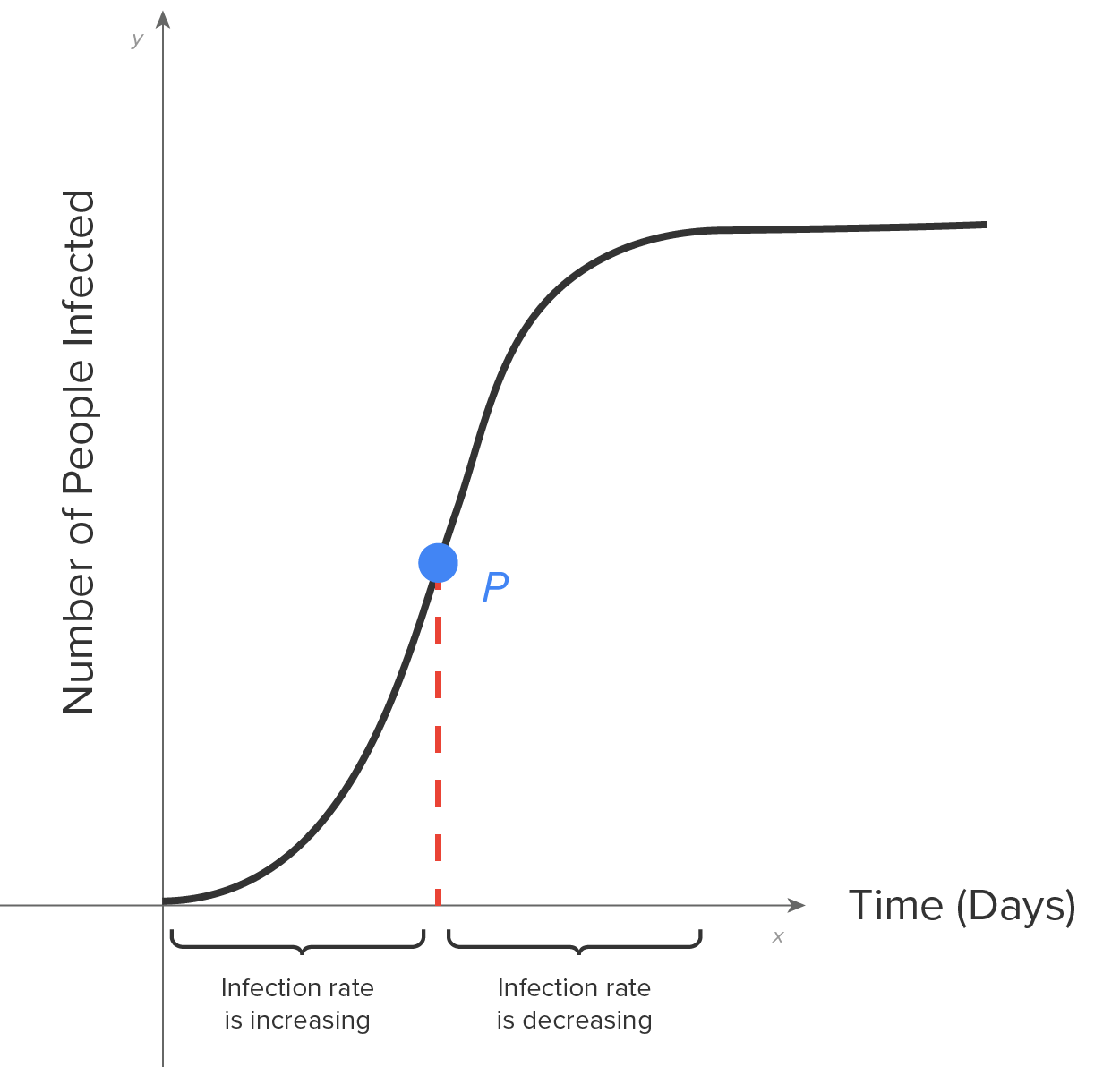
A graph provides data on the number of people infected over time (days), with an x-axis and a y-axis intersecting at the origin. The x-axis represents ‘time (days)’, and the y-axis represents the ‘number of people infected’. A vertical dashed line extends from the x-axis to a marked point labeled ‘p’, representing the inflection point. An S-shaped curve rises from the origin, passes through the point ‘P’— where the infection rate transitions from increasing to decreasing—and then levels off, running horizontally toward the end. The section of the x-axis from the origin to the dashed line is labeled ‘Infection rate is increasing’, and the section from the dashed line to the rest of the x-axis is labeled ‘Infection rate is decreasing’.

As you can see, the number of cases is increasing over the entire domain.

To the left of point P, the slopes of the tangent lines are increasing. This means that the rate of infection is increasing.

To the right of point P, the slopes of the tangent lines are decreasing. This means that the rate of infection is decreasing.

The inflection point is the transition point between these two events. In terms of disease control, this point is important since it represents the point at which the disease is beginning to get under control.

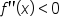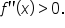
In the last tutorial, you learned that the graph of f open parentheses x close parentheses is concave down when f apostrophe apostrophe open parentheses x close parentheses less than 0 and the graph of f open parentheses x close parentheses is concave up when f apostrophe apostrophe open parentheses x close parentheses greater than 0.

big idea
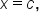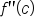As long as f open parentheses x close parentheses is continuous at x equals c comma the graph of f open parentheses x close parentheses could have a point of inflection when f apostrophe apostrophe open parentheses c close parentheses equals 0 or f apostrophe apostrophe open parentheses c close parentheses is undefined. To verify this, make a sign graph of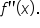 f apostrophe apostrophe open parentheses x close parentheses.

term to know
Inflection Point (Point of Inflection)
A point on a curve at which concavity changes.

2. Determining the Inflection Points of a Function

EXAMPLE

Consider the function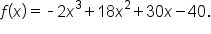 f open parentheses x close parentheses equals short dash 2 x cubed plus 18 x squared plus 30 x minus 40. Find any points of inflection.

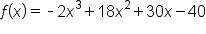
f open parentheses x close parentheses equals short dash 2 x cubed plus 18 x squared plus 30 x minus 40 Start with the original function; the domain is all real numbers.
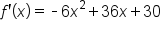
f apostrophe open parentheses x close parentheses equals short dash 6 x squared plus 36 x plus 30 Take the first derivative.
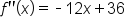
f apostrophe apostrophe open parentheses x close parentheses equals short dash 12 x plus 36 Take the second derivative.
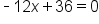
short dash 12 x plus 36 equals 0 Any inflection points could occur when 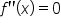f apostrophe apostrophe open parentheses x close parentheses equals 0. (Note: f apostrophe apostrophe open parentheses x close parentheses is never undefined.)
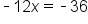
short dash 12 x equals short dash 36 Subtract 36 from both sides.
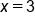
x equals 3 Divide both sides by -12.

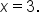
Therefore, there could be a point of inflection when x equals 3.

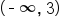Now, select one number (called a test value) inside the intervals open parentheses short dash infinity comma space 3 close parentheses and open parentheses 3 comma space infinity close parentheses to determine the sign of f apostrophe apostrophe open parentheses x close parentheses on that interval:

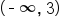
Interval open parentheses short dash infinity comma space 3 close parentheses open parentheses 3 comma space infinity close parentheses
Test Value 0 4
Value of bold italic f bold apostrophe bold apostrophe open parentheses bold x close parentheses bold equals bold short dash bold 12 bold italic x bold plus bold 36 36 -12
Behavior of bold italic f open parentheses bold x close parentheses Concave up Concave down

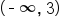Therefore, f open parentheses x close parentheses is concave up on the interval open parentheses short dash infinity comma space 3 close parentheses and concave down on the interval 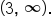open parentheses 3 comma space infinity close parentheses. Thus, a point of inflection occurs when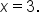 x equals 3.

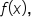On the graph of f open parentheses x close parentheses comma the inflection point is located at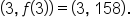 open parentheses 3 comma space f open parentheses 3 close parentheses close parentheses equals open parentheses 3 comma space 158 close parentheses.

Let’s take a look at a different function.

EXAMPLE

Consider the function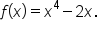 f open parentheses x close parentheses equals x to the power of 4 minus 2 x. Find any points of inflection.

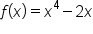
f open parentheses x close parentheses equals x to the power of 4 minus 2 x Start with the original function; the domain is all real numbers.
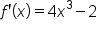
f apostrophe open parentheses x close parentheses equals 4 x cubed minus 2 Take the first derivative.
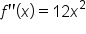
f apostrophe apostrophe open parentheses x close parentheses equals 12 x squared Take the second derivative.
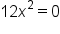
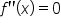12 x squared equals 0 Any inflection points could occur when f apostrophe apostrophe open parentheses x close parentheses equals 0. (Note: f apostrophe apostrophe open parentheses x close parentheses is never undefined.)
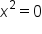
x squared equals 0 Divide both sides by 12.
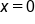
x equals 0 Take the square root of both sides.

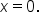
Therefore, an inflection point possibly occurs when x equals 0.

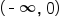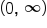Now, select one number (called a test value) inside the intervals open parentheses short dash infinity comma space 0 close parentheses and open parentheses 0 comma space infinity close parentheses to determine the sign of f apostrophe apostrophe open parentheses x close parentheses on that interval:

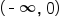
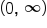
Interval open parentheses short dash infinity comma space 0 close parentheses open parentheses 0 comma space infinity close parentheses
Test Value -1 1
Value of 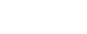bold italic f bold apostrophe bold apostrophe open parentheses bold x close parentheses bold equals bold 12 bold italic x to the power of bold 2 12 12
Behavior of 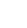bold italic f open parentheses bold x close parentheses Concave up Concave up

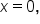Since the concavity does not change at x equals 0 comma there is no inflection point when 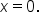x equals 0. Since there were no other possible points of inflection, 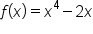f open parentheses x close parentheses equals x to the power of 4 minus 2 x has no points of inflection. As you can see, the graph is always concave up.

A graph with an x-axis and a y-axis ranging from −6 to 6. The graph has a parabolic curve that extends downward from the second quadrant, passing through (0, 0), (1, −1), then extending upward into the first quadrant.

watch
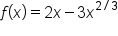In this video, we’ll analyze the function f open parentheses x close parentheses equals 2 x minus 3 x to the power of 2 divided by 3 end exponent for points of inflection.

summary
In this lesson, you learned that the point of inflection is defined as the point on a curve where it transitions between being concave up and concave down (and the tangent line exists). This point is useful in modeling an epidemic, for example, since it can represent the point at which the disease is beginning to get under control. 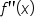You also learned that to determine the inflection points of a function, first find all values in the domain of f open parentheses x close parentheses where f apostrophe apostrophe open parentheses x close parentheses is either 0 or undefined, then use a graph of the signs of f apostrophe apostrophe left parenthesis x right parenthesis to determine the x-values where inflection points occur.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Inflection Point (Point of Inflection)

A point on a curve at which concavity changes.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.