Table of Contents |
You have 60 pieces of candy to give a group of x people, and you want to distribute them evenly.
If there are 13 people in the room, then each person would get 60/13 = 4.615… pieces of candy. Since this is impossible and you want to be fair to each person, you would give each person 4 pieces of candy, with some left over.
So, what would be a mathematical rule for this situation?
Let 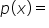 the number of pieces of candy each person receives when there are x people.
the number of pieces of candy each person receives when there are x people.
Then, the value of 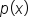 is found as follows:
is found as follows:
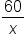 is a whole number, then use
is a whole number, then use 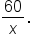
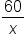 is not a whole number, then use the next whole number less than
is not a whole number, then use the next whole number less than 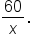
This leads us to a need to define another function, called the greatest integer function, which is denoted 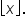 The piecewise definition of
The piecewise definition of  is as follows:
is as follows:

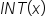
|
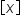
|
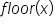
|
Here are a few function values for 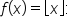
| Function Statement | Reasoning |
|---|---|
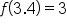
|
Since 3.4 is not an integer, the function returns the greatest integer below 3.4, which is 3. |
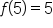
|
Since 5 is an integer, the function returns 5. |
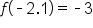
|
Since -2.1 is not an integer, the function returns the greatest integer that is below -2.1, which is -3. |
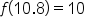
|
Since 10.8 is not an integer, the function returns the greatest integer that is below 10.8, which is 10. |
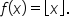

The graph of the basic greatest integer function is shown below.
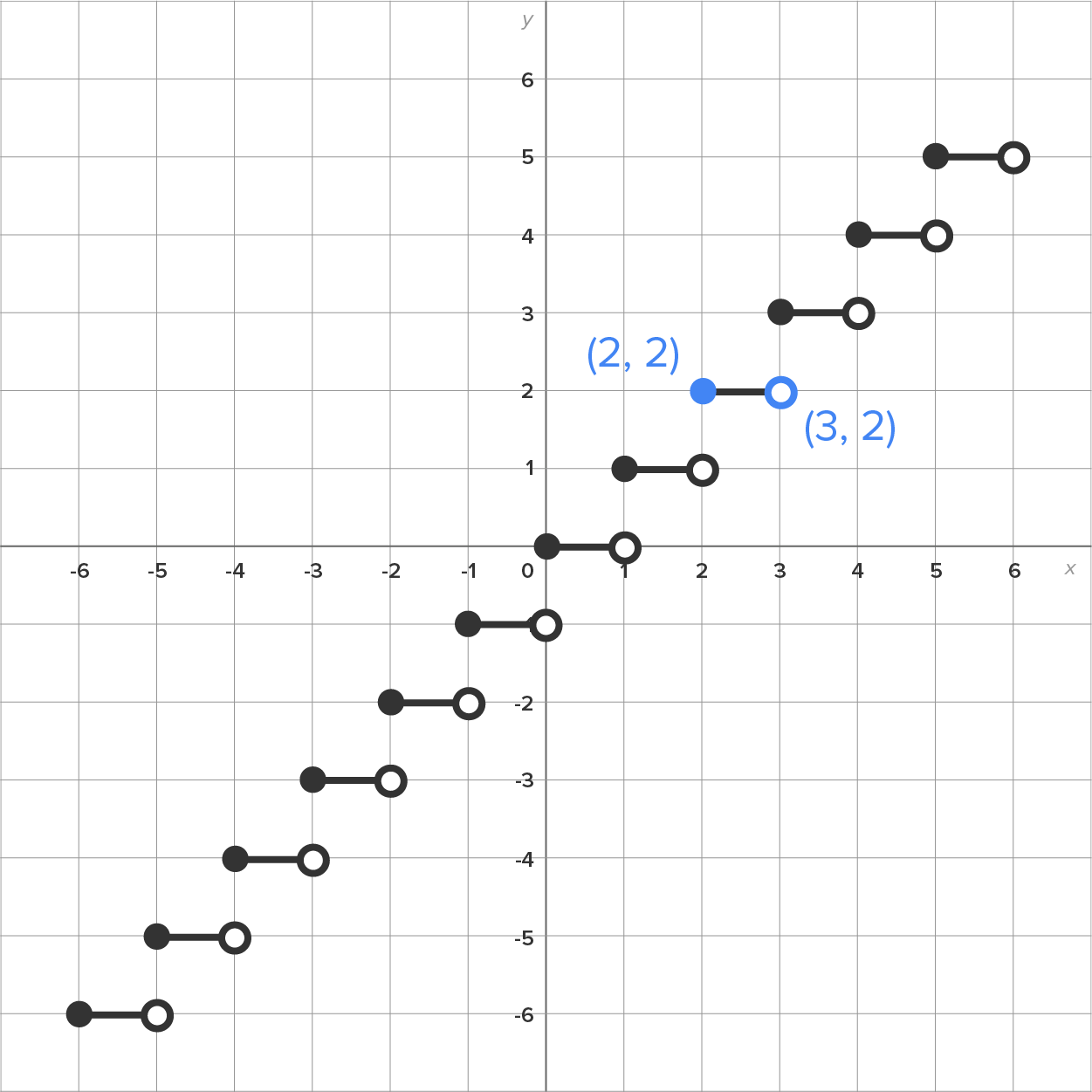
Note, the “stair step” pattern continues indefinitely in both directions.
To understand how this graph works, consider the two points that are labelled 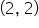 and
and 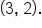 If
If 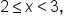 the greatest integer function returns the value of 2. We can see this by using some input-output pairs:
the greatest integer function returns the value of 2. We can see this by using some input-output pairs:

|
2 | 2.2 | 2.5 | 2.8 | 2.9 | 2.99 | 2.999 | 2.9999 |
|---|---|---|---|---|---|---|---|---|

|
2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
|
(2, 2) | (2.2, 2) | (2.5, 2) | (2.8, 2) | (2.9, 2) | (2.99, 2) | (2.999, 2) | (2.9999, 2) |
As soon as the value of x jumps to exactly 3, then the greatest integer function returns a value of 3, which means the graph moves to the next “stair step.”
Let’s now return to the situation where you were handing out candy to a group of x people.
To find the number of pieces, we calculate 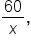 then round down if necessary. This is the essence of a greatest integer function!
then round down if necessary. This is the essence of a greatest integer function!
Using the greatest integer function, the number of pieces received by each person is:
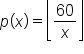
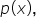 with selected points labelled:
with selected points labelled:
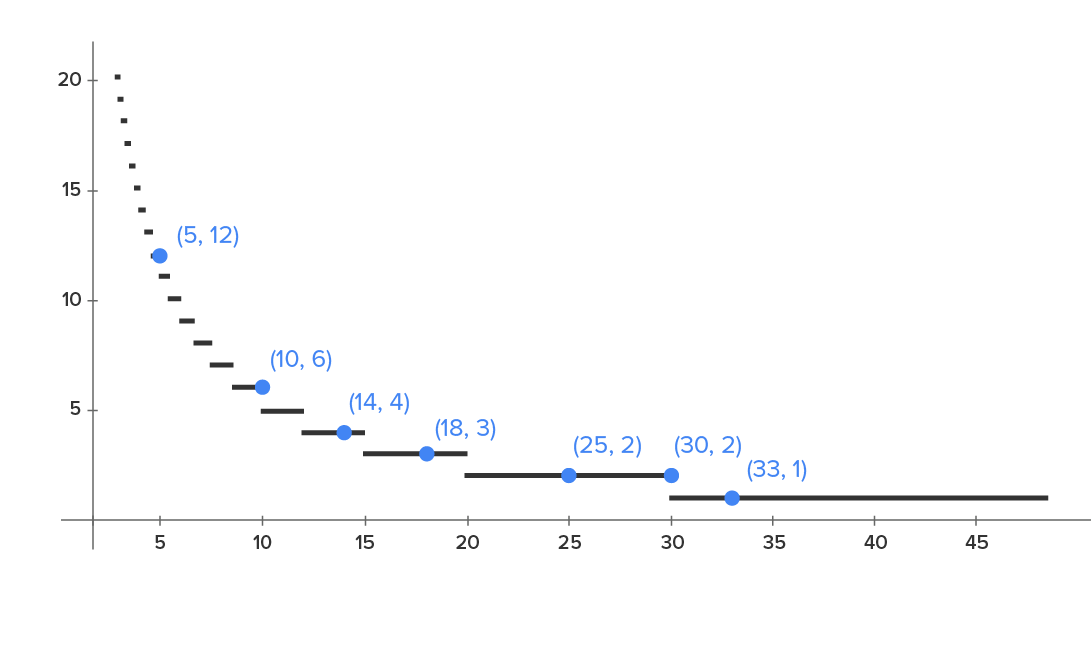
Note, the piece of the graph where 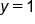 would extend out to the point
would extend out to the point 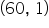 until falling to 0 for
until falling to 0 for 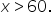 Why is this? If you have more than 60 people in your group and you only have 60 pieces of candy to give out, there is no way to give the same amount of candy to each of them (so each person would receive no candy). On the bright side, that means you get to keep it all.
Why is this? If you have more than 60 people in your group and you only have 60 pieces of candy to give out, there is no way to give the same amount of candy to each of them (so each person would receive no candy). On the bright side, that means you get to keep it all.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.