Table of Contents |
Consider the function 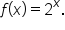 A table of values as well as its graph are shown below.
A table of values as well as its graph are shown below.

|
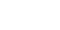
|
|---|---|
| -3 |
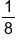
|
| -2 |
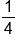
|
| -1 |
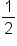
|
| 0 |
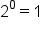
|
| 1 |
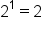
|
| 2 |
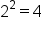
|
| 3 |
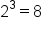
|
| 4 |
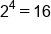
|
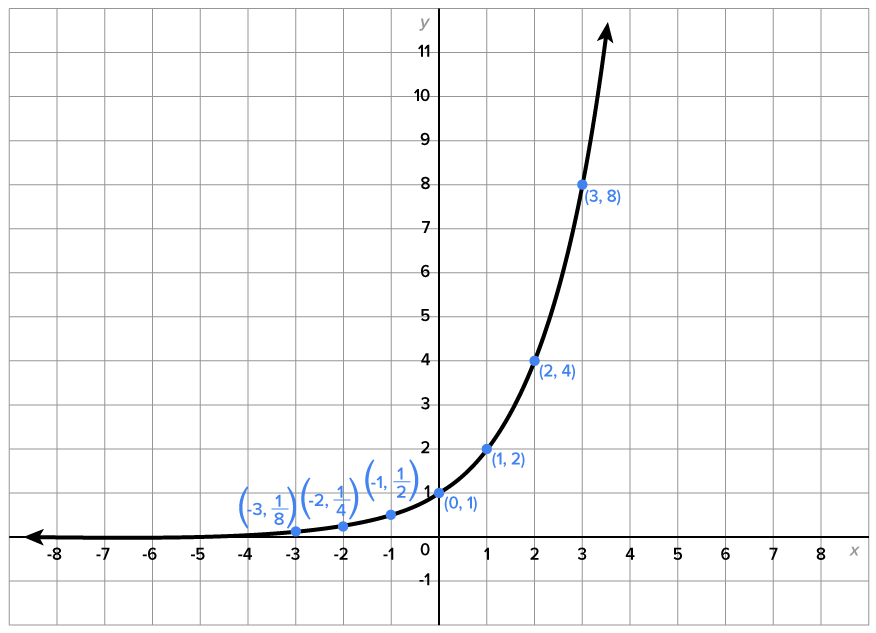
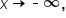
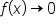 from above, and as
from above, and as 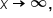
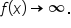
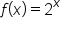 has a horizontal asymptote of
has a horizontal asymptote of 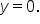
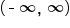 and the range is
and the range is 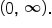
 is
is 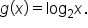 Its table of values and graph are shown below.
Its table of values and graph are shown below.

|
|
|---|---|
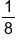
|
-3 |
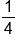
|
-2 |
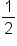
|
-1 |
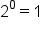
|
0 |
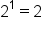
|
1 |
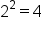
|
2 |
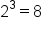
|
3 |
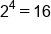
|
4 |
 from the right,
from the right,  , and as
, and as 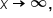
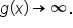
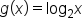 has a vertical asymptote of
has a vertical asymptote of 
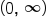 and the range is
and the range is 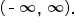
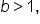 the graph of
the graph of 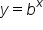 has a shape similar to the graph of
has a shape similar to the graph of 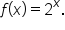 This means that the graph of
This means that the graph of 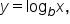 when
when 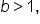 will look similar to the graph of
will look similar to the graph of 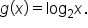 This includes
This includes 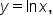 since e is approximately 2.71828, which is greater than 1, and
since e is approximately 2.71828, which is greater than 1, and 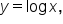 which is base 10.
which is base 10.
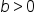 and
and 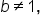 the graph of
the graph of 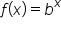 passes through the point
passes through the point 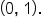 Then, the graph of its inverse,
Then, the graph of its inverse, 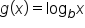 , passes through the point
, passes through the point 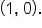
EXAMPLE
Sketch the graph of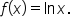

|
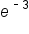
|
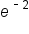
|
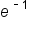
|
1 |
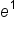
|
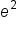
|
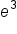
|
|---|---|---|---|---|---|---|---|
Approximate 
|
0.0498 | 0.1353 | 0.3679 | 1 | 2.7183 | 7.3891 | 20.0855 |
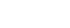
|
-3 | -2 | -1 | 0 | 1 | 2 | 3 |
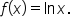 Note the vertical asymptote
Note the vertical asymptote 

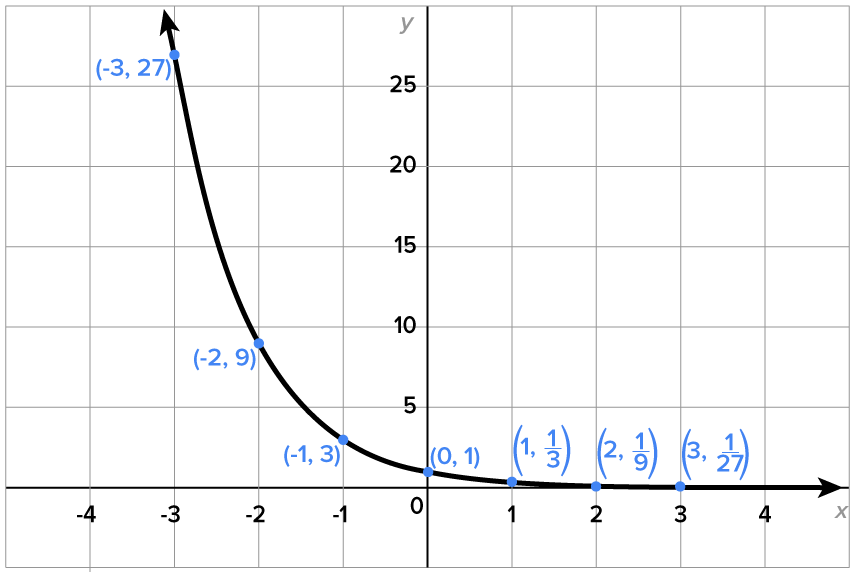
Consider the function 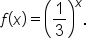 A table of values as well as its graph are shown below.
A table of values as well as its graph are shown below.

|
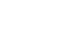
|
|---|---|
| -3 | 27 |
| -2 | 9 |
| -1 | 3 |
| 0 | 1 |
| 1 |
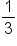
|
| 2 |
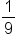
|
| 3 |
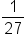
|
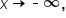
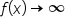 , and as
, and as 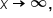
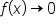 from above.
from above.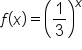 has a horizontal asymptote of
has a horizontal asymptote of 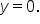
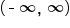 and the range is
and the range is 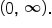
 is
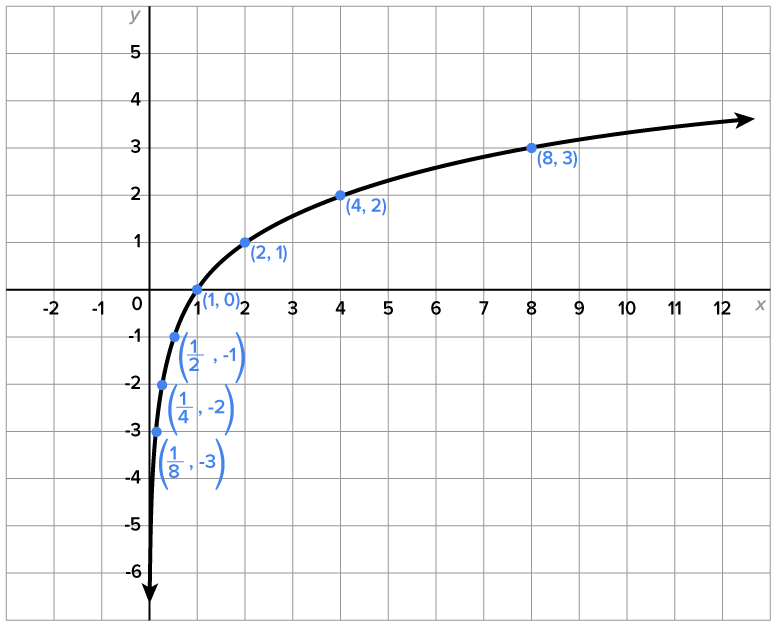
is 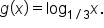 Its table of values and graph are shown below.
Its table of values and graph are shown below.

|

|
|---|---|
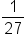
|
3 |
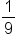
|
2 |
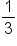
|
1 |
| 1 | 0 |
| 3 | -1 |
| 9 | -2 |
| 27 | -3 |
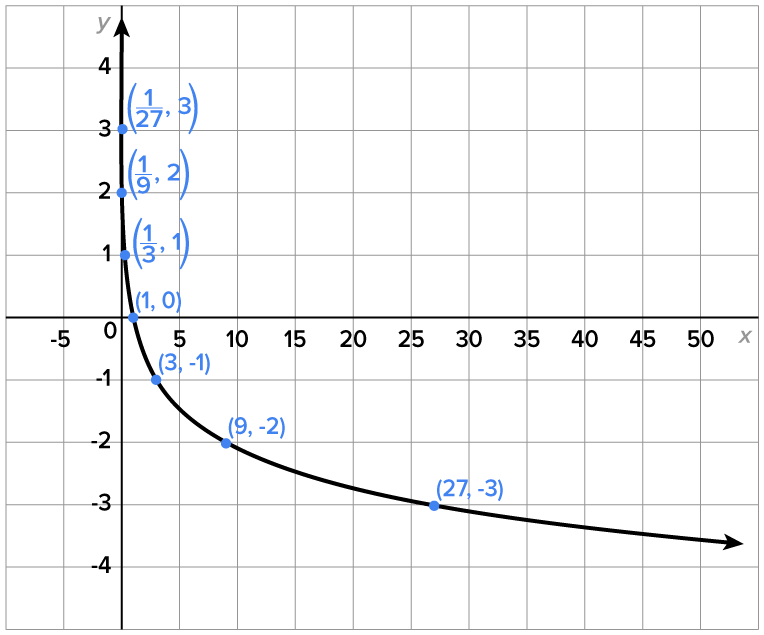
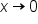 from the right,
from the right, 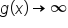 , and as
, and as 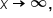

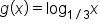 has a vertical asymptote of
has a vertical asymptote of 
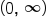 and the range is
and the range is 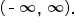
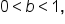 the graph of
the graph of 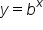 has a shape similar to the graph of
has a shape similar to the graph of 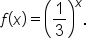 This means that the graph of
This means that the graph of 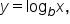 when
when 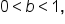 will look similar to the graph of
will look similar to the graph of 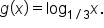
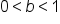 and
and 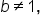 the graph of
the graph of 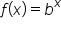 passes through the points
passes through the points 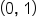 and
and 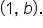 Then, the graph of its inverse,
Then, the graph of its inverse, 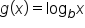 , passes through the points
, passes through the points 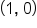 and
and 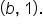 This means that
This means that 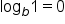 and
and 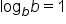 for all values of b such that
for all values of b such that 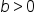 and
and 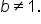
In summary, here are the possible shapes of 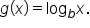

|
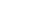
|
|---|---|

|

|
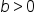 and
and 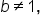 the domain of
the domain of 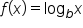 is
is 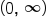 and its range is
and its range is 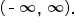 Also note the following:
Also note the following:
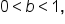 the function is decreasing on its domain.
the function is decreasing on its domain. 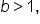 the function is increasing on its domain.
the function is increasing on its domain.Since the graph of a logarithmic function passes the horizontal line test, logarithmic functions are also one-to-one. Then, logarithmic functions also have the inverse property.
The one-to-one property for logarithmic functions tells us that if two logarithmic expressions with the same base are equal to each other, then the arguments must also be equal. It also tells us that if two quantities are equal, their logarithms in the same base are also equal. This property will be used more frequently when solving equations.
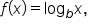 where
where 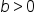 and
and 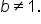 Then, for quantities R and S,
Then, for quantities R and S, 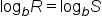 if and only if
if and only if 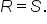
Now that we know what the graph of a logarithmic function looks like, we can observe relationships between different graphs.
First, let’s compare two logarithmic graphs with different bases.
EXAMPLE
In this example, we’ll graph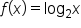 and
and 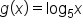 on the same pair of axes.
on the same pair of axes.

|
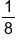
|
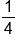
|
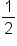
|
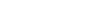
1 | 2 | 4 | 8 |
|---|---|---|---|---|---|---|---|
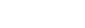
|
-3 | -2 | -1 | 0 | 1 | 2 | 3 |

|
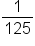
|
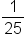
|
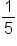
|
1 | 5 | 25 | 125 |
|---|---|---|---|---|---|---|---|
|
-3 | -2 | -1 | 0 | 1 | 2 | 3 |
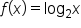 and the thicker graph is
and the thicker graph is 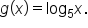
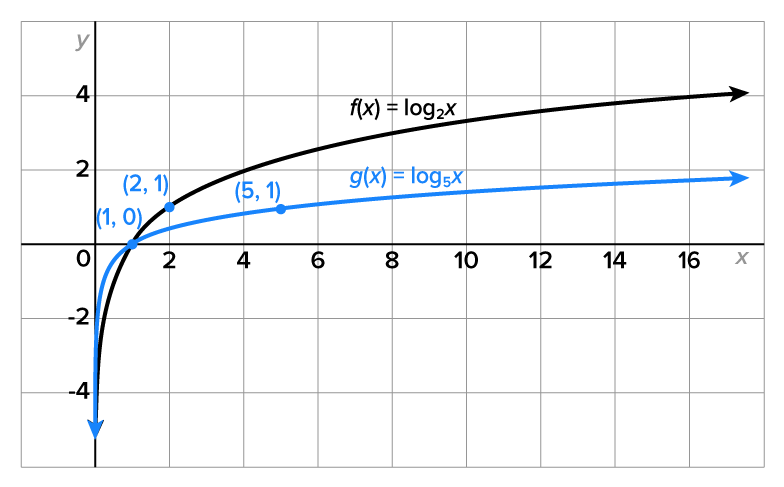
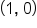 and have vertical asymptote
and have vertical asymptote 
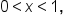 the graph of g is above the graph of f.
the graph of g is above the graph of f. 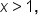 the graph of f is above the graph of g.
the graph of f is above the graph of g. 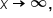 the logarithmic function with the smaller base will be above the graph of the logarithmic function with the larger base. Later in this course, we will actually see that the graphs of f and g are constant multiples of one another.
the logarithmic function with the smaller base will be above the graph of the logarithmic function with the larger base. Later in this course, we will actually see that the graphs of f and g are constant multiples of one another.
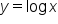 and the other is
and the other is 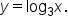

Let’s now do an exploration where we compare two logarithmic functions, but this time, the bases are reciprocals of each other.
EXAMPLE
Consider the functions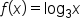 and
and 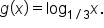 The table below shows their values for selected values of x.
The table below shows their values for selected values of x.

|
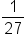
|
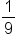
|
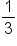
|
1 | 3 | 9 | 27 |
|---|---|---|---|---|---|---|---|
|
-3 | -2 | -1 | 0 | 1 | 2 | 3 |

|
3 | 2 | 1 | 0 | -1 | -2 | -3 |
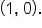
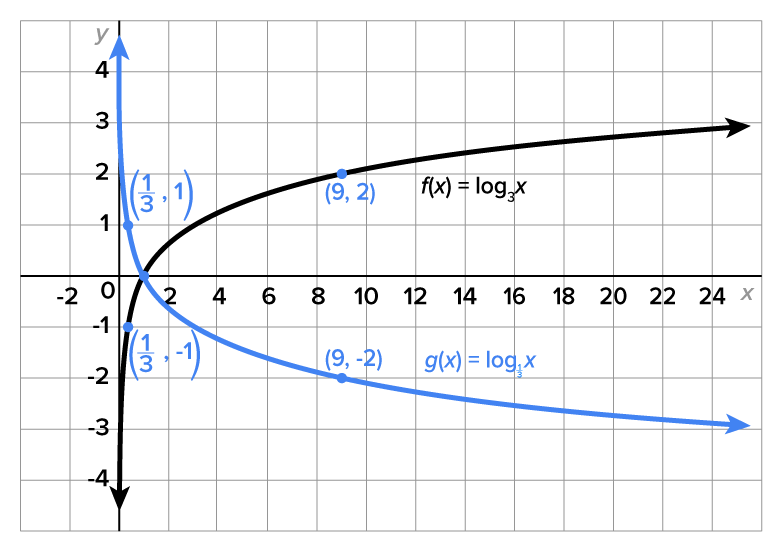
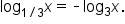
As a result of the last example, we have the following.
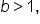
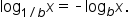
This result is important since it establishes a correspondence between logarithms with bases that are reciprocals of each other. Going forward, you’ll notice that all applications seen in this course (and in future courses) use bases that are larger than 1. This is because the common and natural logarithms both use bases that are larger than 1.
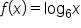 and
and 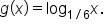
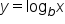 and
and 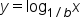 are reflections of each other over the x-axis. Because of this fact, we focus on logarithmic functions with bases that are greater than 1. This way, we can still reference the natural and common logarithms.
are reflections of each other over the x-axis. Because of this fact, we focus on logarithmic functions with bases that are greater than 1. This way, we can still reference the natural and common logarithms.
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS