
Table of Contents |
Recall that 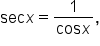 meaning that if the value of
meaning that if the value of 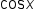 is known, then
is known, then 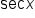 is its reciprocal.
is its reciprocal.
Consider now this table of values.

|
0 |
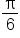
|
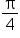
|
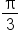
|
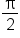
|
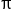
|
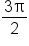
|
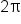
|
|---|---|---|---|---|---|---|---|---|

|
1 |
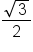
|
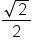
|
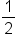
|
0 | -1 | 0 | 1 |

|
1 |
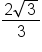
|
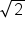
|
2 | undef. | -1 | undef. | 1 |
Since 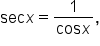 we can build the graph of the secant function from the cosine function, as shown in the figure below.
we can build the graph of the secant function from the cosine function, as shown in the figure below.
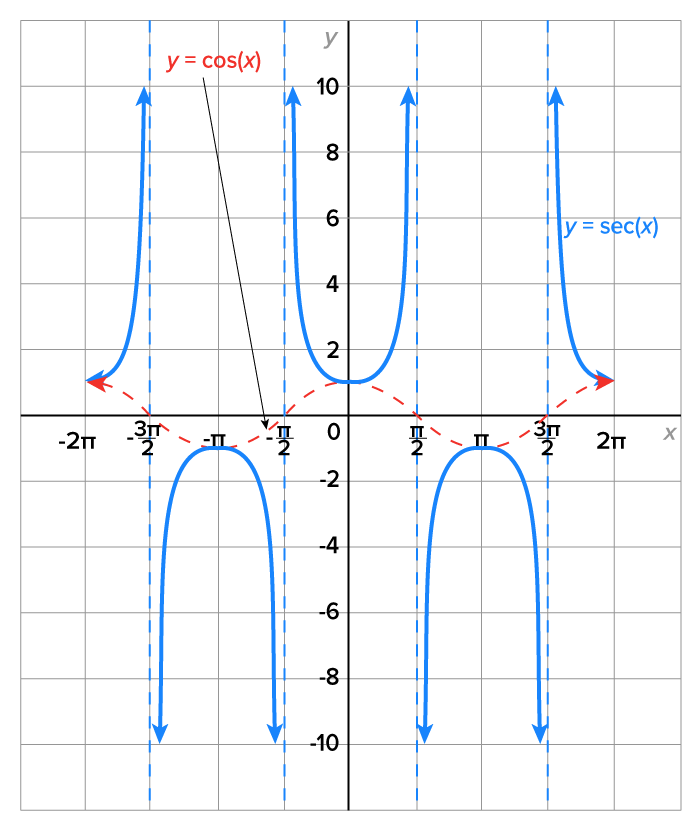
Properties of the graph:
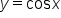 has its x-intercepts.
has its x-intercepts. 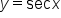 is the set of all real numbers excluding odd multiples of
is the set of all real numbers excluding odd multiples of 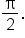
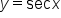 is
is 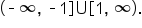
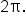
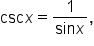 meaning that if the value of
meaning that if the value of 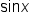 is known, then
is known, then 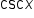 is its reciprocal.
is its reciprocal.
Consider now this table of values.

|
0 |
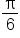
|
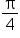
|
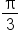
|
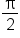
|
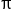
|
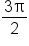
|
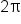
|
|---|---|---|---|---|---|---|---|---|

|
0 |
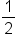
|
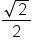
|
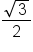
|
1 | 0 | -1 | 0 |

|
undef. | 2 |
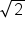
|
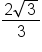
|
1 | undef. | -1 | undef. |
Since 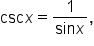 we can build the graph of the cosecant function from the sine function, as shown in the figure below.
we can build the graph of the cosecant function from the sine function, as shown in the figure below.
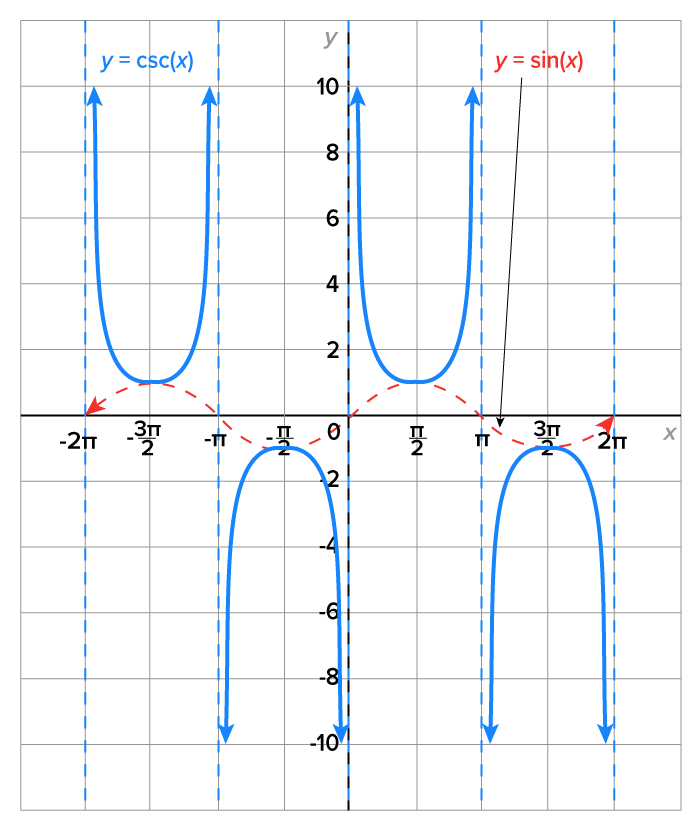
Properties of the graph:
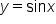 has its x-intercepts.
has its x-intercepts. 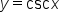 is the set of all real numbers excluding integer multiples of
is the set of all real numbers excluding integer multiples of 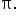
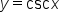 is
is 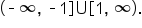
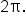
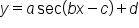 and
and 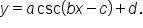
 is not related to amplitude since the secant and cosecant graphs are not bounded. This value simply determines vertical stretch or compression, and a reflection over the x-axis if
is not related to amplitude since the secant and cosecant graphs are not bounded. This value simply determines vertical stretch or compression, and a reflection over the x-axis if 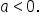
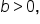 the period is
the period is 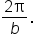
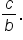

Before getting to the graphs of the tangent and cotangent functions, the figure below shows the unit circle with angles  and
and 
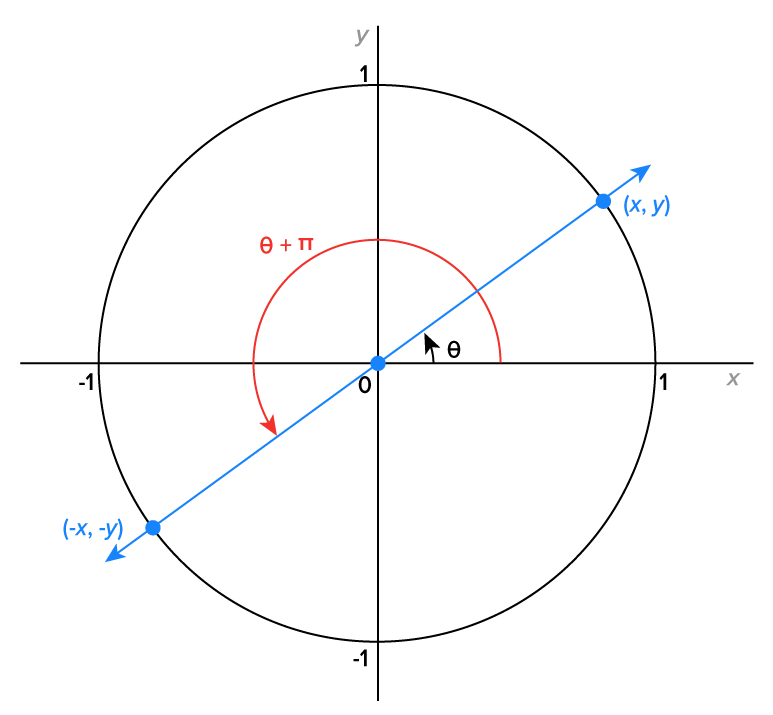
Assuming that 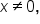 recall that
recall that 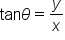 when the terminal side of angle
when the terminal side of angle  intercepts the unit circle at the point
intercepts the unit circle at the point 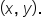
Then, for the angles  and
and 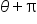 in the figure, we have
in the figure, we have 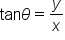 and
and 
In general, this means that when 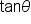 is defined, then
is defined, then 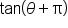 has the same value.
has the same value.
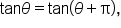 this means that the period of the tangent function is
this means that the period of the tangent function is 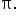
Note that the value of the tangent function is the slope of the line containing the points 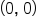 and
and 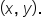
Recall also that 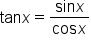 and that
and that 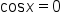 when x is any odd multiple of
when x is any odd multiple of 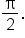 Then,
Then, 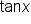 is undefined when x is any odd multiple of
is undefined when x is any odd multiple of 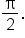
The graph of the function 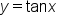 is shown below.
is shown below.
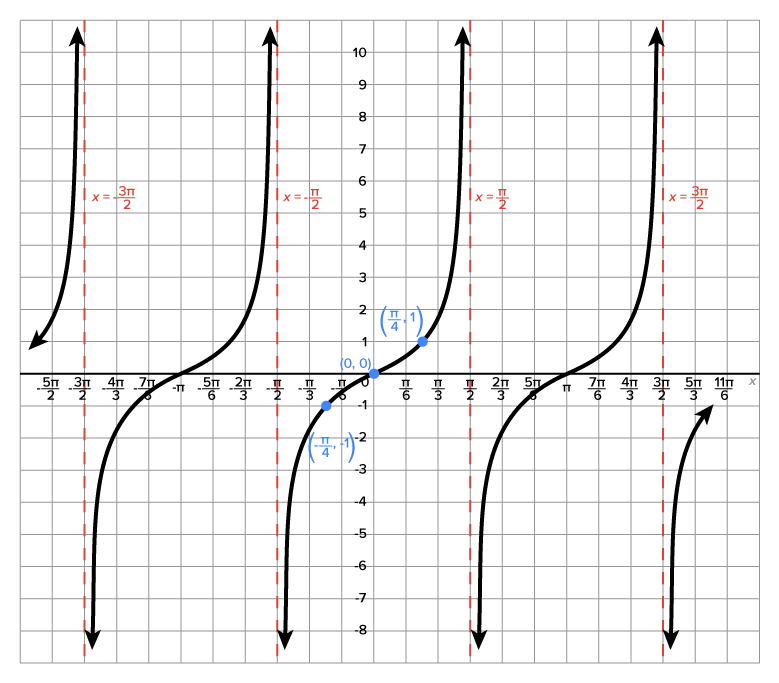
Properties of the graph:
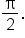
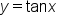 is the set of all real numbers excluding multiples of
is the set of all real numbers excluding multiples of 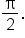
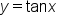 is
is 
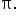
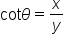 when the terminal side of angle
when the terminal side of angle  intercepts the unit circle at the point
intercepts the unit circle at the point 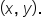
Since these are reciprocal values of the tangent function, the basic cotangent function also has a period of 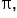 meaning that
meaning that 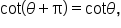 as long as
as long as 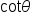 is defined.
is defined.
Since 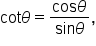 the cotangent function is undefined for all values of
the cotangent function is undefined for all values of  where
where 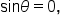 or
or 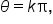 where k is an integer.
where k is an integer.
All of this information considered, below is the graph of 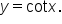 Even though it is not marked with a dashed line, there is also a vertical asymptote at
Even though it is not marked with a dashed line, there is also a vertical asymptote at 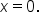
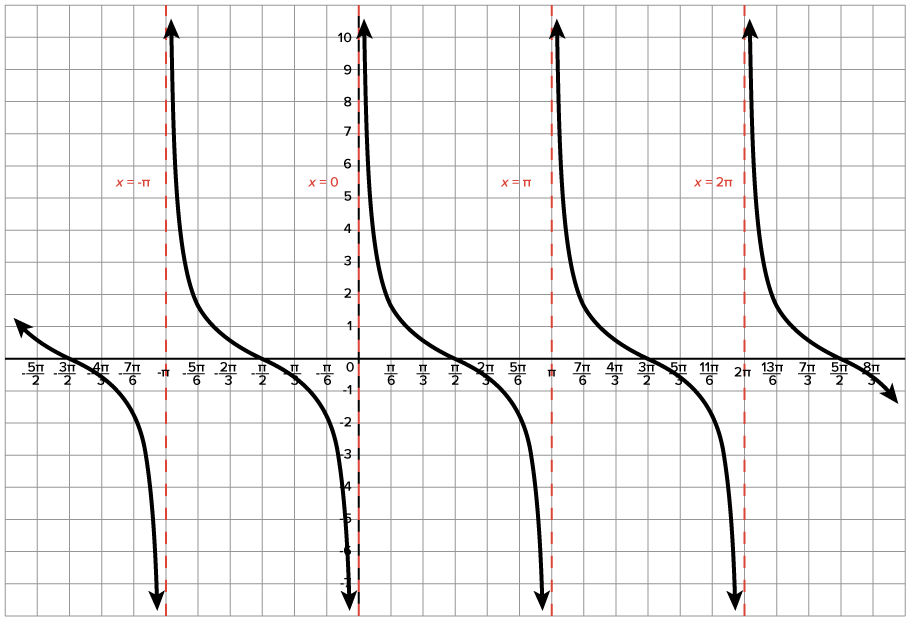
Properties of the graph:
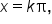 where k is an integer.
where k is an integer. 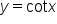 is the set of all real numbers excluding integer multiples of
is the set of all real numbers excluding integer multiples of 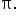
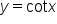 is
is 
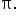
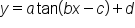 and
and 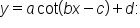
 is not related to amplitude since the tangent and cotangent graphs are not bounded. This value simply determines vertical stretch or compression, and a reflection over the x-axis if
is not related to amplitude since the tangent and cotangent graphs are not bounded. This value simply determines vertical stretch or compression, and a reflection over the x-axis if 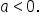
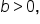 the period is
the period is 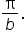
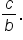
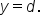

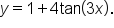
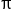 rather than
rather than 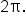
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.