Table of Contents |
Consider the unit circle shown below, with all points corresponding to special angles and multiples of special angles labeled.
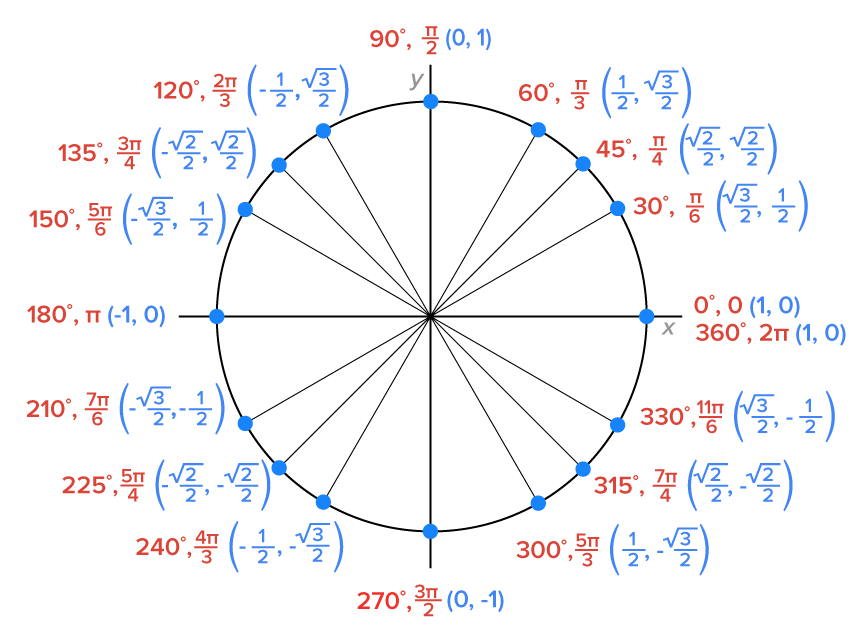
As  increases from one quadrantal angle to the next, the behavior of
increases from one quadrantal angle to the next, the behavior of  is shown in the table.
is shown in the table.
As  Increases From: Increases From:
|
 (y-coordinate): (y-coordinate):
|
|---|---|
0 to 
|
increases from 0 to 1 |
 to to 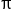
|
decreases from 1 to 0 |
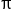 to to 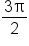
|
decreases from 0 to -1 |
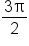 to to 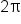
|
increases from -1 to 0 |
We’re going to use this information to sketch the graph of the sine function in the xy-coordinate system.
Let 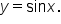 The table above means that the graph of
The table above means that the graph of 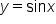 has the following key points:
has the following key points:
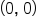
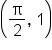
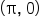
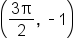


|
0 |
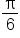
|
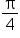
|
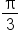
|
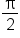
|
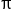
|
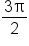
|
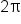
|
|---|---|---|---|---|---|---|---|---|

|
0 |
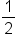
|
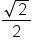
|
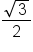
|
1 | 0 | -1 | 0 |
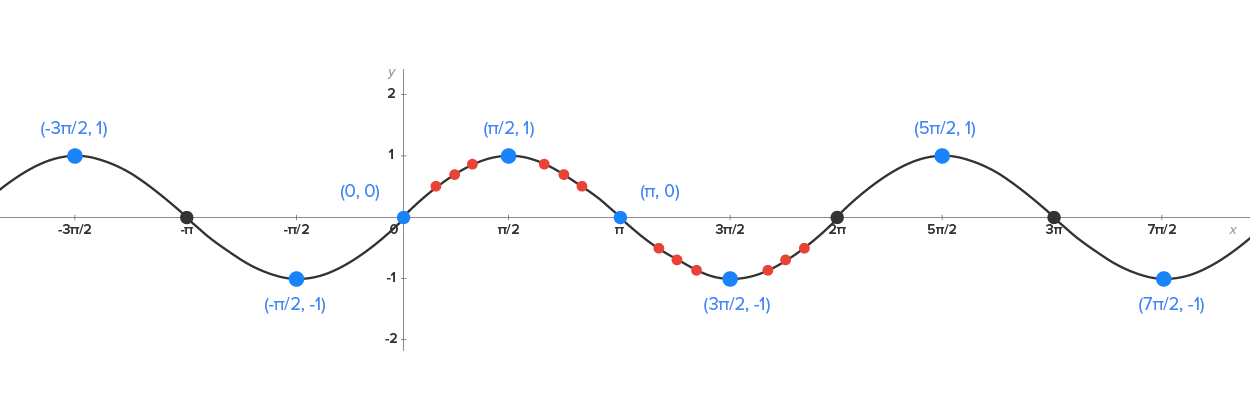
Using these points, the graph of 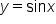 on the interval
on the interval 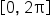 is shown below.
is shown below.
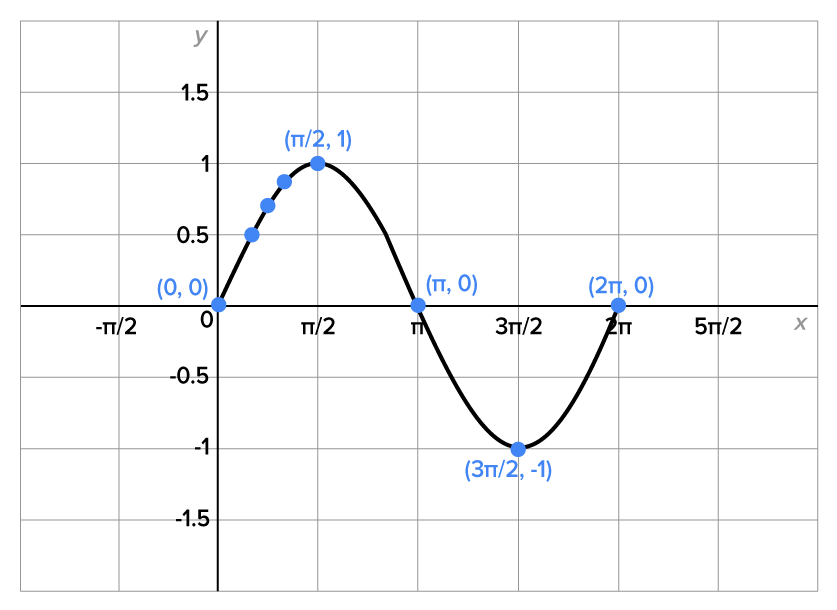
This is the most important period of the sine graph, since all other periods repeat this one. Note again the key points on the graph:
| Key Point |
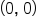
|
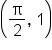
|
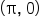
|
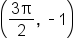
|

|
|---|---|---|---|---|---|
| Description | Starting point, x-intercept | Maximum | x-intercept | Minimum point | x-intercept |
The following are properties of one period of the basic sine graph:
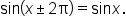 Because of this relationship, we say that the sine function has a period of
Because of this relationship, we say that the sine function has a period of 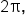 meaning that the values of
meaning that the values of 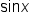 are equal when x is increased or decreased by a multiple of
are equal when x is increased or decreased by a multiple of 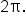 As a result, the complete graph of
As a result, the complete graph of 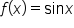 is shown below.
is shown below.
The graph continues in this pattern indefinitely. Since there are no breaks or holes in the graph, the domain of 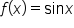 is the set of all real numbers, also written in interval notation as
is the set of all real numbers, also written in interval notation as  The range of this function is
The range of this function is 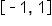 since the smallest output value is -1 and the largest output value is 1.
since the smallest output value is -1 and the largest output value is 1.
Recall from an earlier lesson that the sine function is odd, meaning that 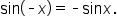 In the xy-coordinate system, this means that the graph is symmetric with respect to the origin.
In the xy-coordinate system, this means that the graph is symmetric with respect to the origin.
Since  is the “middle value,” we call the line
is the “middle value,” we call the line  the horizontal midline, which is the line that represents the average of the maximum and minimum values of the function.
the horizontal midline, which is the line that represents the average of the maximum and minimum values of the function.
Now, let’s examine the cosine function.
As  increases from one quadrantal angle to the next, the behavior of
increases from one quadrantal angle to the next, the behavior of  is shown in the table.
is shown in the table.
As  Increases From: Increases From:
|
 (x-coordinate): (x-coordinate):
|
|---|---|
0 to 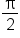
|
decreases from 1 to 0 |
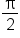 to to 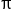
|
decreases from 0 to -1 |
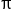 to to 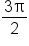
|
increases from -1 to 0 |
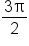 to to 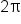
|
increases from 0 to 1 |
We’re going to use this information to sketch the graph of the cosine function in the xy-coordinate system.
Let 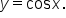 The table above means that the graph of
The table above means that the graph of 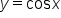 has the following key points:
has the following key points:
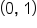

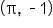
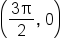
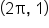

|
0 |
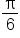
|
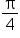
|
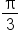
|
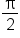
|
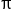
|
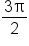
|
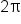
|
|---|---|---|---|---|---|---|---|---|

|
1 |
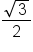
|
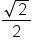
|
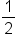
|
0 | -1 | 0 | 1 |
Recall that 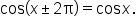 Because of this relationship, we say that the cosine function has a period of
Because of this relationship, we say that the cosine function has a period of 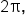 meaning that the values of
meaning that the values of 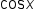 are equal when x is increased or decreased by a multiple of
are equal when x is increased or decreased by a multiple of 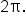 As a result, the complete graph of
As a result, the complete graph of 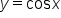 is shown below.
is shown below.
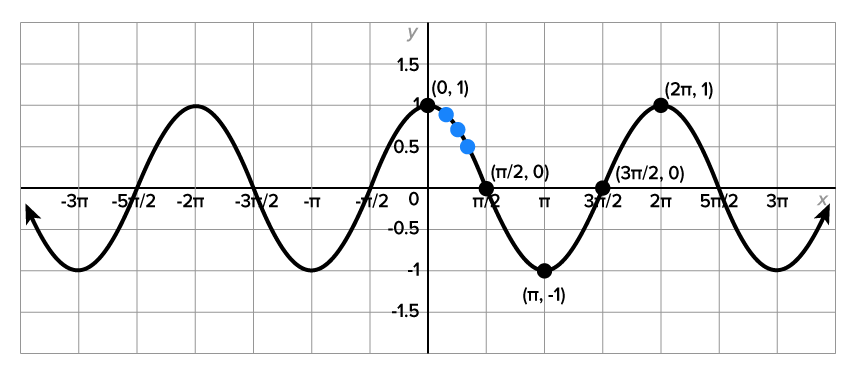
Recall from an earlier lesson that the cosine function is even, meaning that 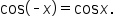 In the xy-coordinate system, this means that the graph is symmetric with respect to the y-axis.
In the xy-coordinate system, this means that the graph is symmetric with respect to the y-axis.
The most important period of the cosine graph is the one that starts at 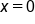 and ends at
and ends at 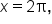 since all other periods repeat this one. Note again the key points on the graph:
since all other periods repeat this one. Note again the key points on the graph:
| Key Point |
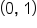
|

|
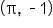
|
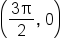
|

|
|---|---|---|---|---|---|
| Description | Starting point, maximum value | x-intercept | Minimum point | Ending point, x-intercept | Maximum value |
The following are properties of one period of the basic cosine graph:
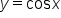 is the set of all real numbers, also written in interval notation as
is the set of all real numbers, also written in interval notation as  The range of this function is
The range of this function is 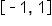 since the smallest output value is -1 and the largest output value is 1.
since the smallest output value is -1 and the largest output value is 1.
The graphs of sine and cosine functions are used to model several real-life situations, such as heights of ocean waves and seasonal temperatures. Graphs that resemble sine and cosine graphs are called sinusoidal graphs, or sinusoids.
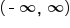 and range
and range 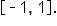 Both functions have a period equal to
Both functions have a period equal to 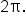 The horizontal midline of each graph is
The horizontal midline of each graph is 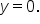
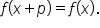 In other words, if the graph of
In other words, if the graph of  is shifted horizontally by p units to the left or to the right, the result is the original graph.
is shifted horizontally by p units to the left or to the right, the result is the original graph. A sinusoidal function has equation 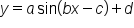 or
or 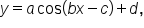 where
where 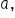 b, c, and d are real numbers with
b, c, and d are real numbers with 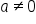 and
and 
In the next two parts, we’ll see what the roles of 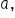 b, c, and d have in shaping the graphs of
b, c, and d have in shaping the graphs of 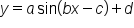 or
or 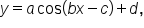 as compared to
as compared to 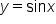 and
and 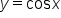 , respectively.
, respectively.
Recall that for some nonzero constant 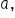 the graph of
the graph of 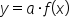 is a vertical stretch of the graph of
is a vertical stretch of the graph of 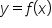 if
if 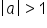 and a vertical compression if
and a vertical compression if 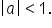 If
If 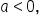 then the graph is also reflected over the x-axis.
then the graph is also reflected over the x-axis.
Consider the graph of 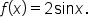 Its graph, along with the graph of
Its graph, along with the graph of 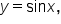 is shown below.
is shown below.
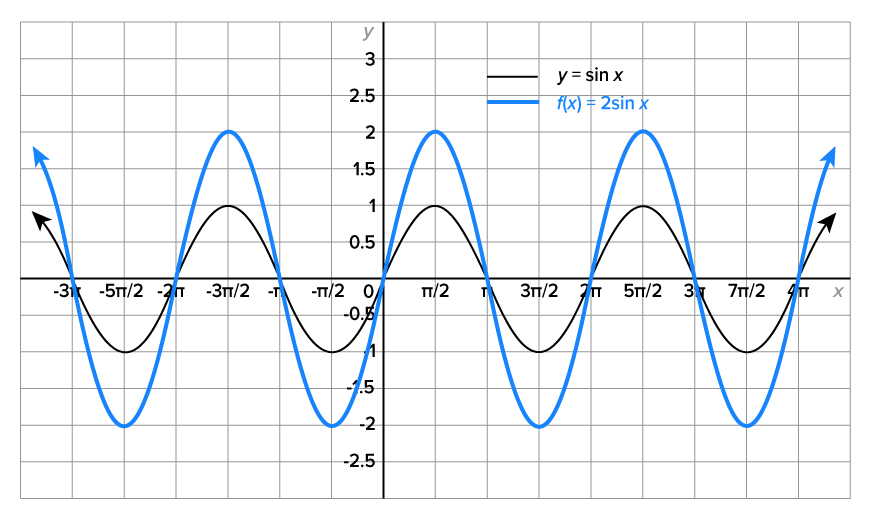
The graph of 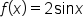 is a vertical stretch of the graph of
is a vertical stretch of the graph of 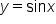 by a factor of 2. Note that the domain is
by a factor of 2. Note that the domain is 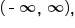 the range is
the range is 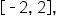 and the period is
and the period is 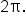
Now consider the graph of 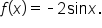 Its graph, along with the graph of
Its graph, along with the graph of 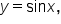 is shown below.
is shown below.
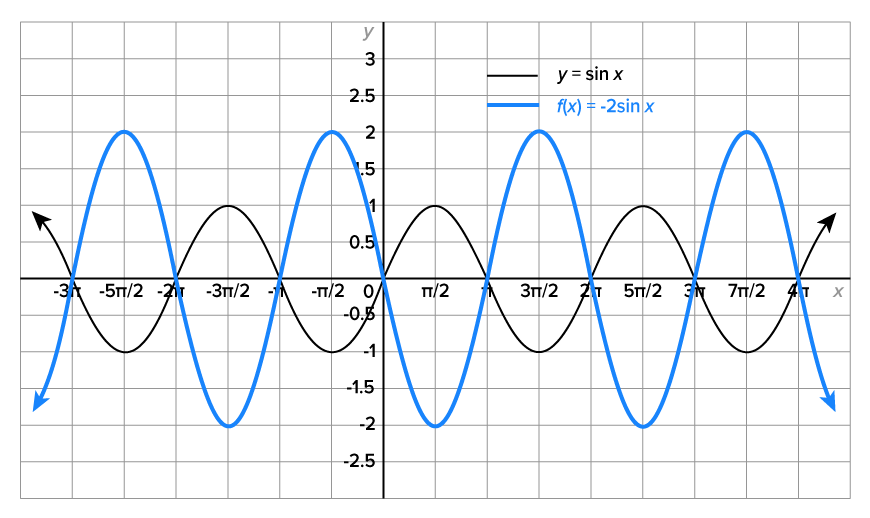
The graph of 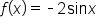 is a vertical stretch of the graph of
is a vertical stretch of the graph of 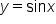 by a factor of 2 and is also reflected over the x-axis. Note that the domain is
by a factor of 2 and is also reflected over the x-axis. Note that the domain is 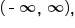 the range is
the range is 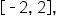 and the period is
and the period is 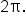
Lastly, consider the graph of 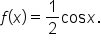 Its graph, along with the graph of
Its graph, along with the graph of  is shown below.
is shown below.
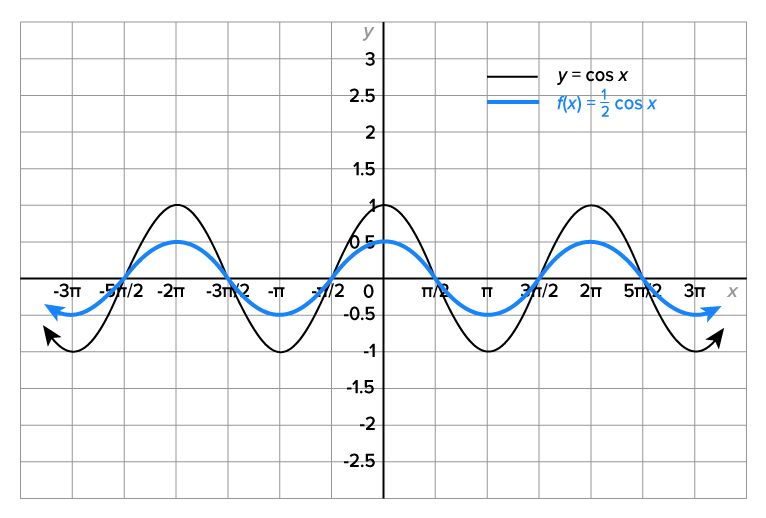
The graph of 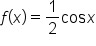 is a vertical compression of the graph of
is a vertical compression of the graph of 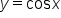 by a factor of
by a factor of 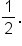 Note that the domain is
Note that the domain is 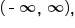 the range is
the range is 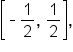 and the period is
and the period is 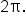
To better describe the vertical stretch factor, we define the amplitude of a sinusoidal graph.
Then, the graphs of 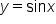 and
and 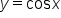 have amplitude 1.
have amplitude 1.
Now consider the graphs of 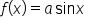 and
and 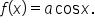 From the examples above, when
From the examples above, when 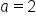 or
or 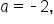 the amplitude is 2. When
the amplitude is 2. When 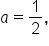 the amplitude is
the amplitude is 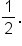
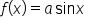 and
and 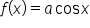 have amplitude
have amplitude 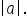
We’ll now investigate sinusoidal graphs in the form 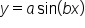 and
and 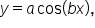 where
where 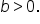
Consider the function 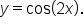
The graphs of 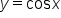 and
and 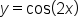 on the interval
on the interval 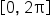 are shown below.
are shown below.
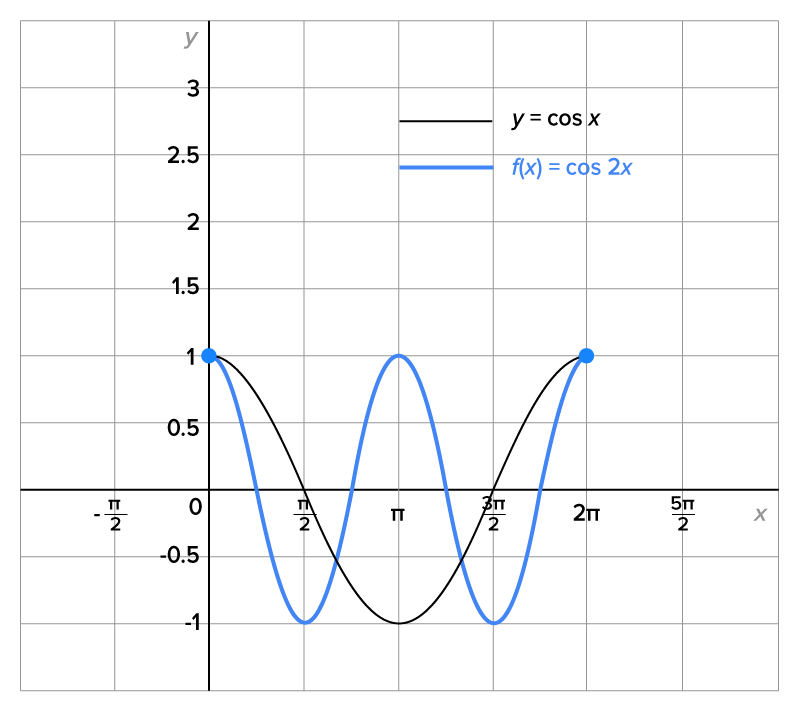
The graph of 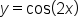 undergoes two complete cycles between
undergoes two complete cycles between 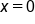 and
and 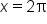 and its first complete cycle between
and its first complete cycle between 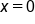 and
and 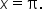
This means that the period of 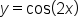 is
is 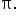
In general, suppose 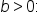
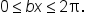
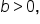 divide all three parts by b, which gives
divide all three parts by b, which gives 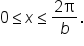
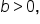 the graph of either
the graph of either 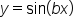 or
or 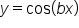 has period
has period 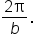
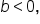 then the even/odd identities can be used to rewrite the trigonometric function so that the angle contains a positive coefficient of the variable.
then the even/odd identities can be used to rewrite the trigonometric function so that the angle contains a positive coefficient of the variable.
EXAMPLE
Consider the equation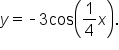
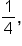 the period of the function is
the period of the function is 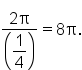
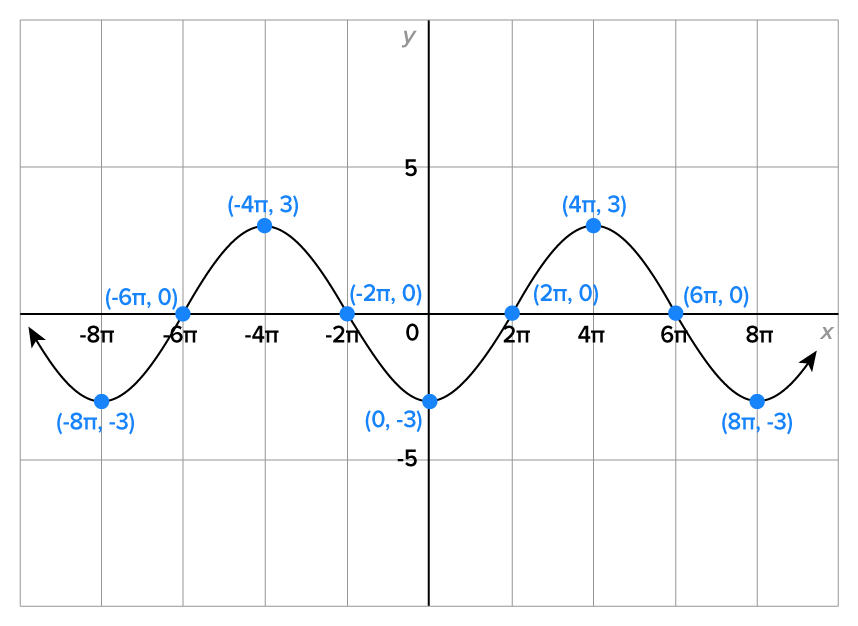
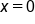 to
to 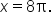
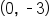 and
and 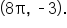
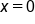 and
and 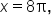 which is at
which is at 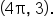
 and
and 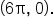
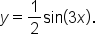
Recall that the graph of 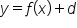 is a vertical shift of d units above the graph of
is a vertical shift of d units above the graph of 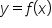 if
if 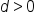 and d units below the graph of
and d units below the graph of 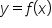 if
if 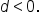
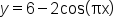 relates to the graph of
relates to the graph of 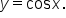
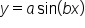 and
and 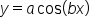 have midline
have midline 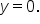 When the graph shifts vertically by d units, the midline shifts along with it, and becomes
When the graph shifts vertically by d units, the midline shifts along with it, and becomes 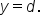
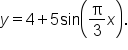
Given the graph of 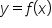 and a positive constant k:
and a positive constant k:
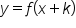 shifts the graph to the left k units.
shifts the graph to the left k units. 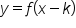 shifts the graph to the right k units.
shifts the graph to the right k units.For example, consider the equations 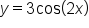 and
and 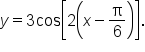
The graph of 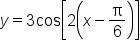 is a horizontal translation to the right
is a horizontal translation to the right 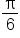 units from the graph of
units from the graph of 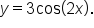
Note: the function 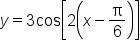 could also be written
could also be written 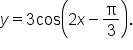 When there is a coefficient of x in the expression for the angle, it may need to be factored out in order to find the phase shift.
When there is a coefficient of x in the expression for the angle, it may need to be factored out in order to find the phase shift.
EXAMPLE
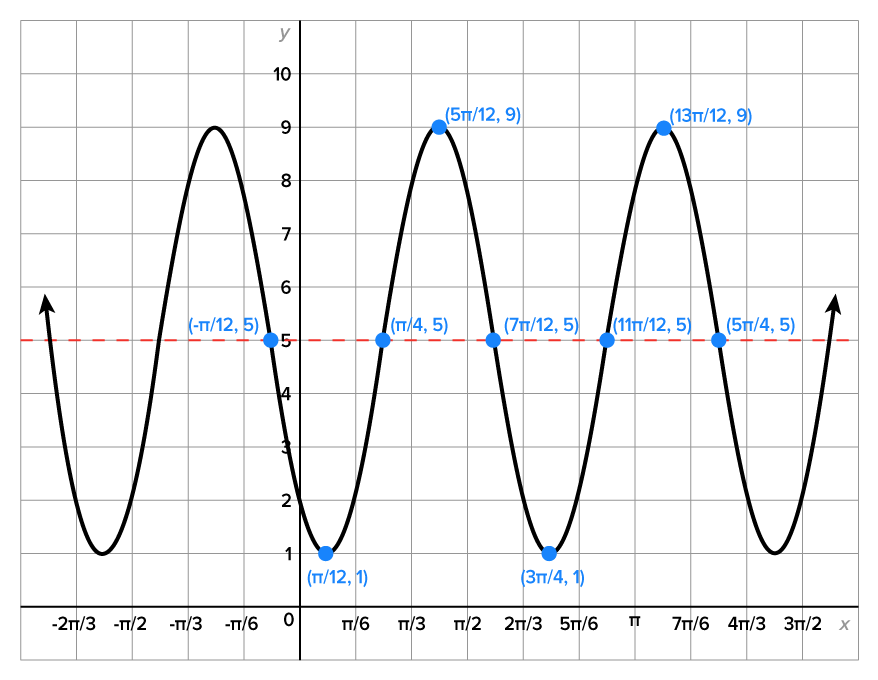
Consider the equation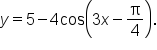
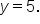 This also means that the minimum and maximum values shift upward 5 units to 1 and 9, respectively.
This also means that the minimum and maximum values shift upward 5 units to 1 and 9, respectively. 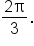
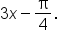
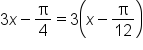
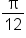 units to the right.
units to the right. 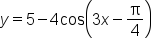 , along with the midline,
, along with the midline,  are shown below.
are shown below.
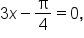 which gives
which gives 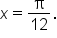 This result tells you that the point with x-coordinate
This result tells you that the point with x-coordinate 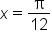 is the new “start” of the curve, which indicates a phase shift of
is the new “start” of the curve, which indicates a phase shift of 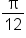 units to the right since the original starting place was
units to the right since the original starting place was 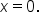
In general, given the graph of 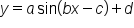 or
or 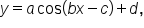 consider the angle
consider the angle 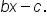 Factoring out b, we obtain
Factoring out b, we obtain 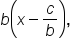 which indicates a phase shift of
which indicates a phase shift of 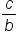 units.
units.
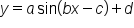 or
or 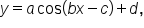 the phase shift is
the phase shift is 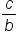 units. A negative value indicates a shift to the left, while a positive value indicates a shift to the right.
units. A negative value indicates a shift to the left, while a positive value indicates a shift to the right.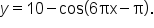
Using the aspects of a sinusoidal graph that we discussed earlier, we can write the equation of a sinusoidal function given its graph.
The goal is to write a function in the form 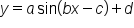 or
or 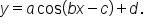 The goal is to use the most convenient curve, which means avoiding a phase shift, if possible.
The goal is to use the most convenient curve, which means avoiding a phase shift, if possible.
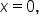 then use a cosine function.
then use a cosine function. 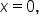 then use a sine function.
then use a sine function. EXAMPLE
Write the equation of the function whose graph is shown in the figure below.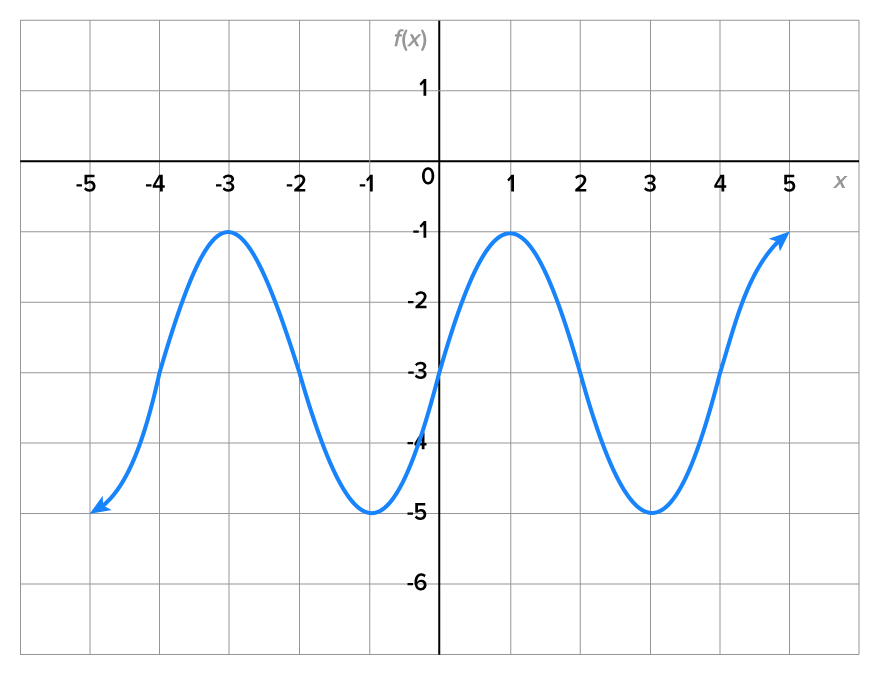
| Property of Graph | Information About Function |
|---|---|
The midline of this graph is 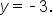
|
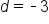
|
The graph passes through the midline at 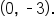
|
The model has the form 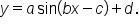 Since the graph passes through its midline at Since the graph passes through its midline at 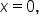 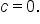
|
| The function has a maximum value of -1 and a minimum value of -5. |
Since the points where the maximum and minimum values occur are two units above and below the midline, the amplitude is 2. Since the graph resembles a non-reflected sine curve, 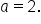
|
| The period of this function is 4. |
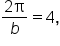 which means which means 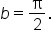
|
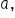 b, c, and d, the equation for the graph is
b, c, and d, the equation for the graph is 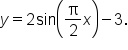
EXAMPLE
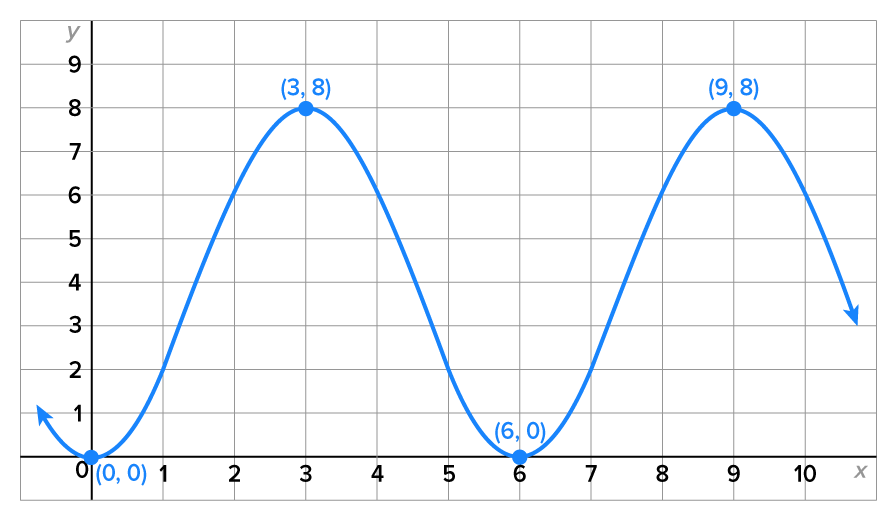
Write the equation of the function whose graph is shown in the figure below.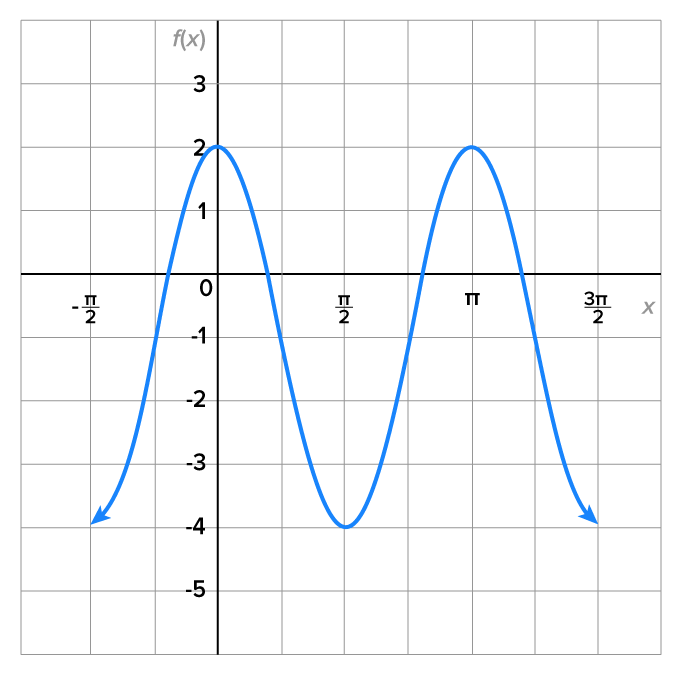
| Property of Graph | Information About Function |
|---|---|
The midline of this graph is 
|
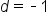
|
The graph attains its maximum value when 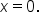
|
This is a non-reflected cosine graph with no phase shift; therefore,  and and 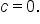 The model has the form 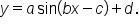
|
| The function has a maximum value of 2 and a minimum value of -4. |
Since these are three units from the midline, the amplitude is 3. Since the graph resembles a non-reflected cosine curve, 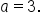
|
The period of this function is 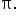
|
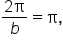 which means which means 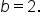
|
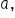 b, c, and d, the equation for the graph is
b, c, and d, the equation for the graph is 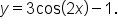
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.