Table of Contents |
When graphing a linear inequality, we generally follow these steps:
| Endpoint IS included in interval | Endpoint IS NOT included in interval |
|---|---|
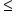 or or 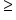
|
< or > |

|

|
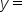 using either a solid or dashed line.
using either a solid or dashed line.
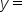 rather than with an inequality symbol. Just remember to use the appropriate line.
rather than with an inequality symbol. Just remember to use the appropriate line.
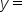 (with the variable y isolated on one side), it is simple enough to once again examine the inequality symbol to see which portion of the coordinate plane to shade.
(with the variable y isolated on one side), it is simple enough to once again examine the inequality symbol to see which portion of the coordinate plane to shade.
EXAMPLE
Graph the linear inequality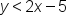 .
.
| Step | Explanation | Graph |
|---|---|---|
| 1. Use solid or dashed line. | To start, we note that the inequality symbol is strict, thus we will use a dashed line. |

|
2. Graph the equation of the line as 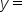 . .
|
Next, we note the y-intercept of -5 and the positive slope of 2 to create the start of our graph. |
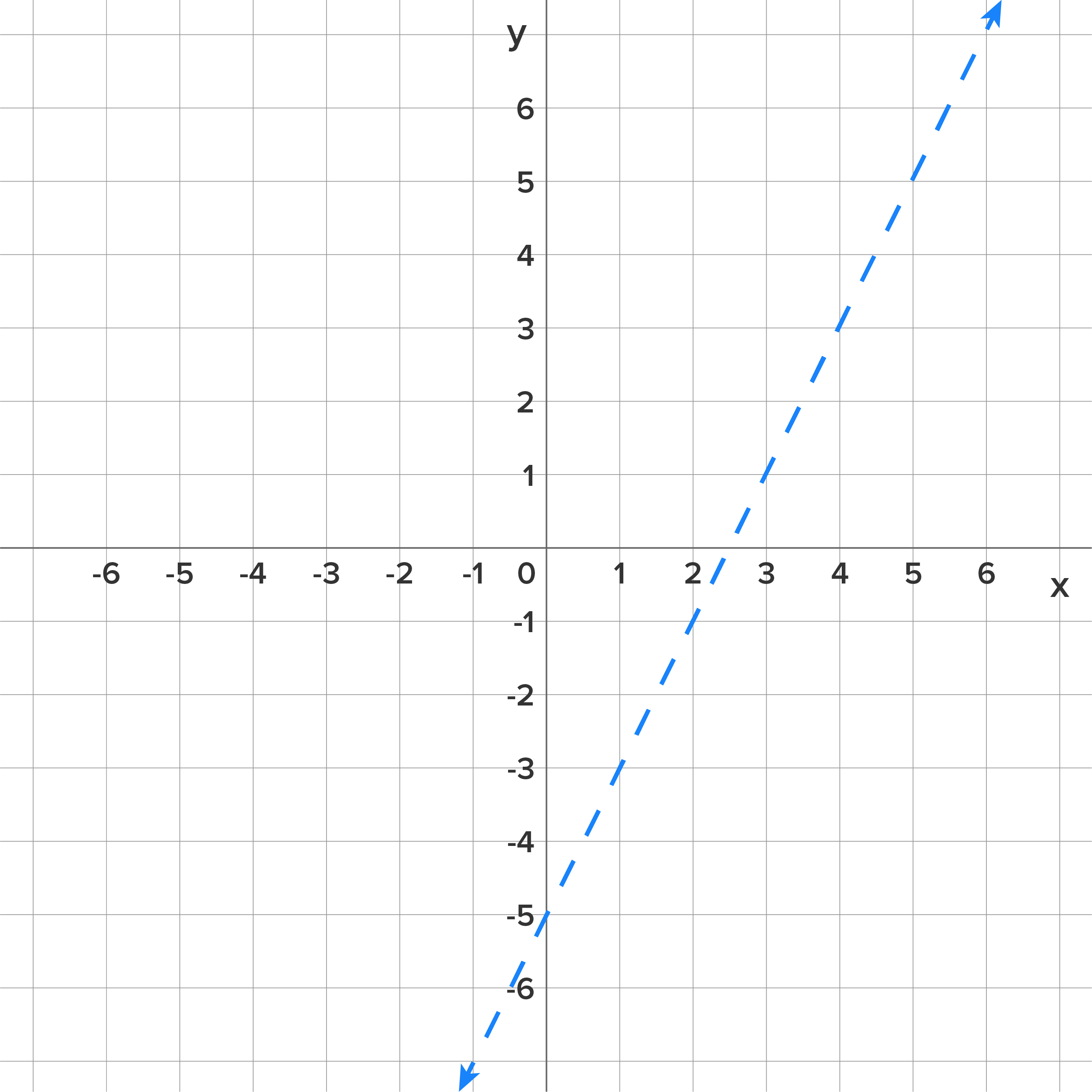
|
| 3. Shade above or below the line. |
Since our inequality is 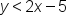 , a less-than inequality, we know to shade everything below our dashed line. , a less-than inequality, we know to shade everything below our dashed line.
|
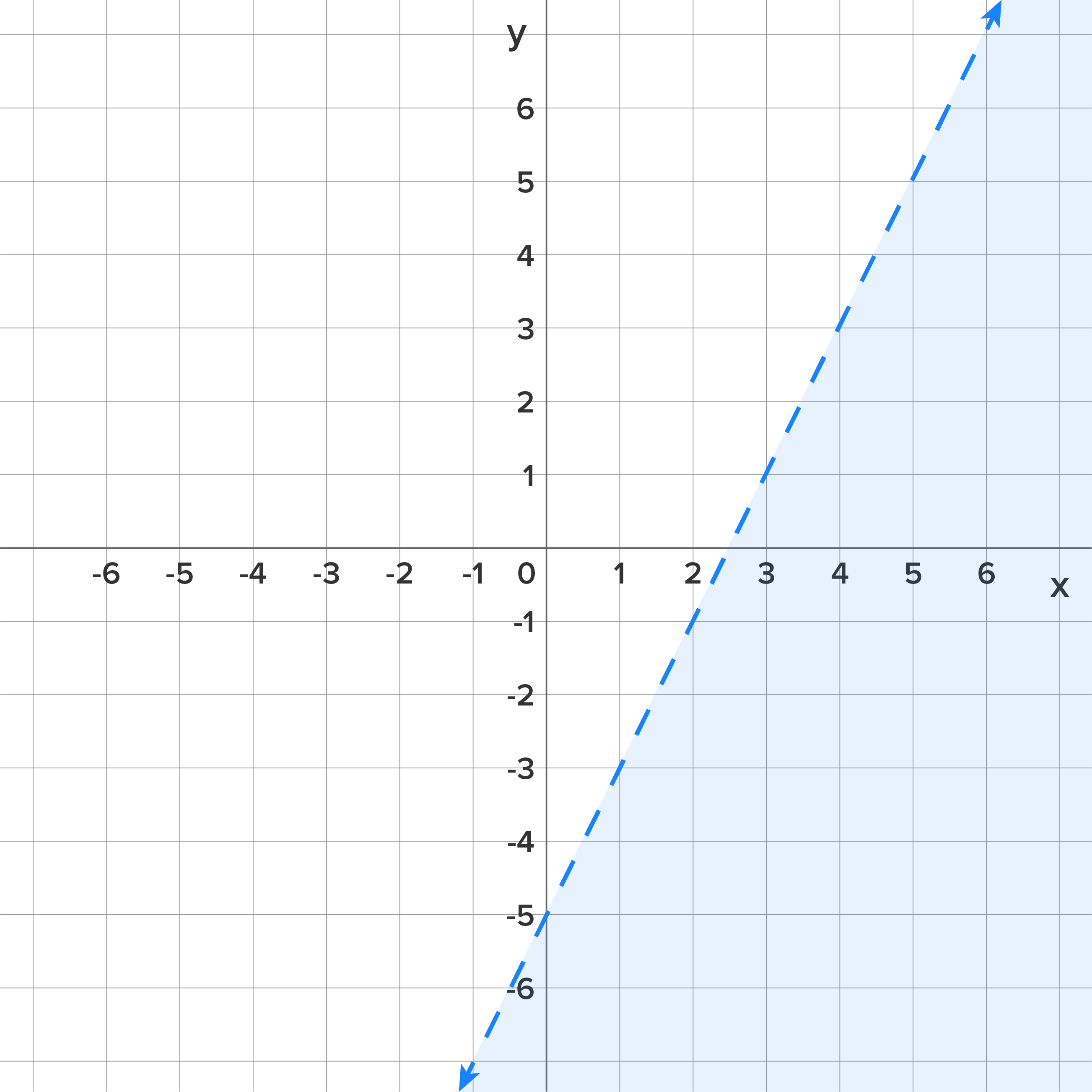
|
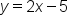 is considered the boundary line, where coordinates on one side of the line are solutions, and coordinates on the other side of the line are non-solutions. The highlighted region is known as the solution region, as it shows all possible x- and y-values that satisfy the inequality.
is considered the boundary line, where coordinates on one side of the line are solutions, and coordinates on the other side of the line are non-solutions. The highlighted region is known as the solution region, as it shows all possible x- and y-values that satisfy the inequality.
Results Driven: Skill in Action |
While using the above method to determine which half of the coordinate plane to shade, there is a more mathematically sound method. This method will be particularly useful when graphing non-linear inequalities, where "above the line" and "below the line" aren't as clear cut.
A test point is any coordinate (x, y) that does not lie on the boundary line. We can think of it as being a representative for all other coordinates on that side of the boundary line. If our test point satisfies the inequality, it represents a solution, as do all the other points on that side. If our test point does not satisfy the inequality, then it represents a non-solution, and the other side of the boundary line should be shaded.
EXAMPLE
Consider the example from above. Suppose we have completed Step 2 and have drawn our boundary line. Now we need to determine which side to shade.
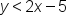
|
Our inequality |
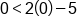
|
Use (0, 0) as our test point. |
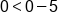
|
Evaluate 2(0). |
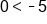
|
Evaluate 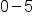 . . 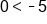 is a false statement, meaning (0, 0) is not in solution region is a false statement, meaning (0, 0) is not in solution region
|

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.