Table of Contents |
The graphs of rational functions have asymptotes, which are lines that aren't part of the curve itself but dictate certain behavior about the curve. The main characteristic of asymptotes is that the curve continues to approach the asymptote at the extreme ends of the graph.
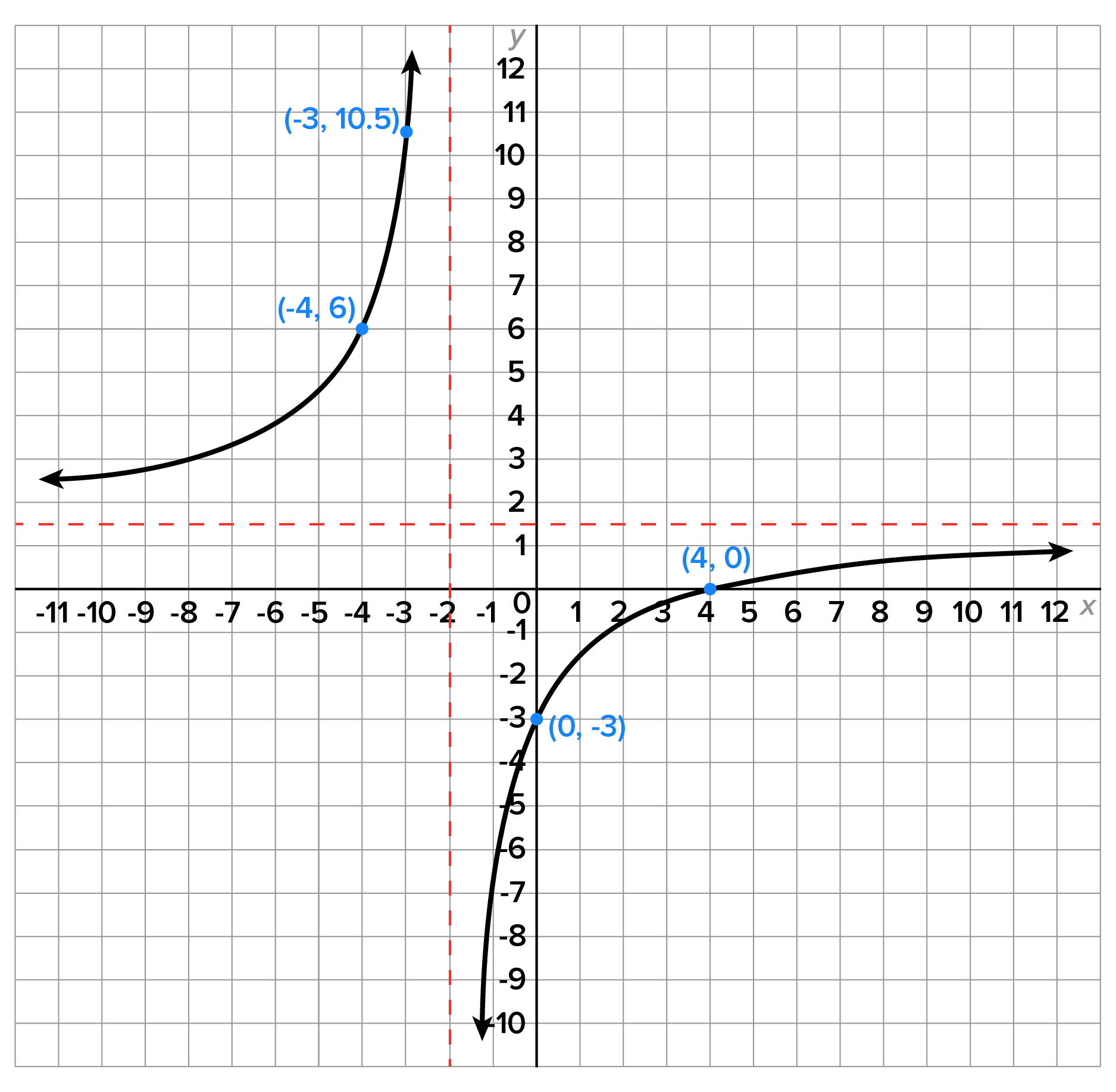
Let's explore three different types of asymptotes on the graphs of rational functions.
One type of asymptote is a vertical asymptote, which is a vertical line that a curve approaches from the left or right.
EXAMPLE
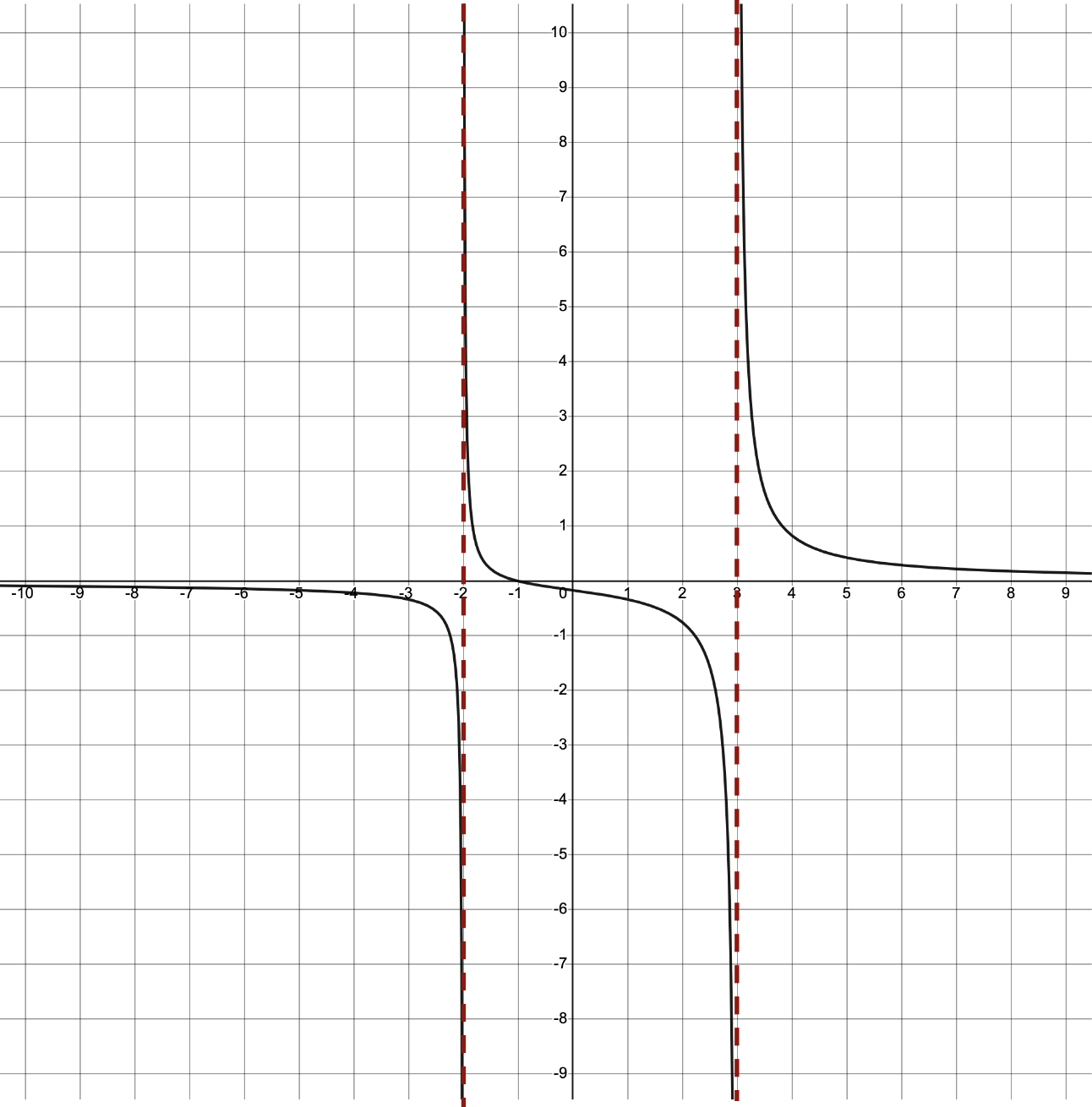
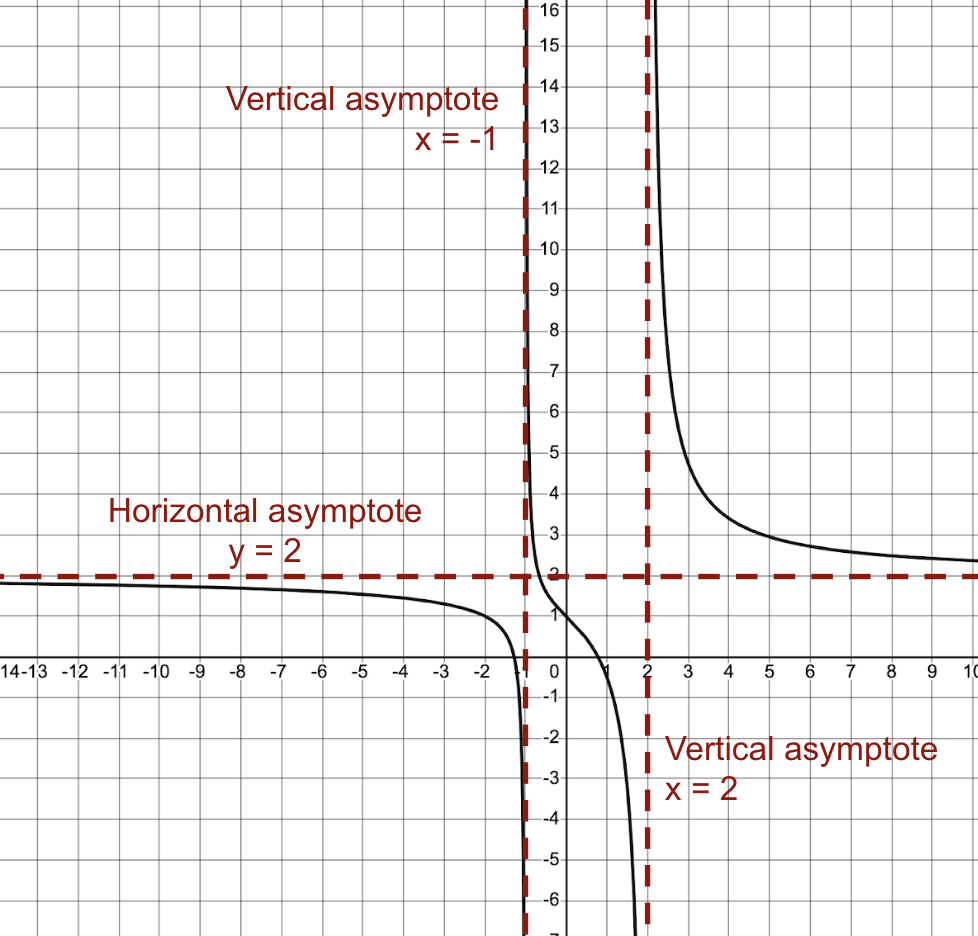
Below is the graph of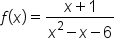 .
.
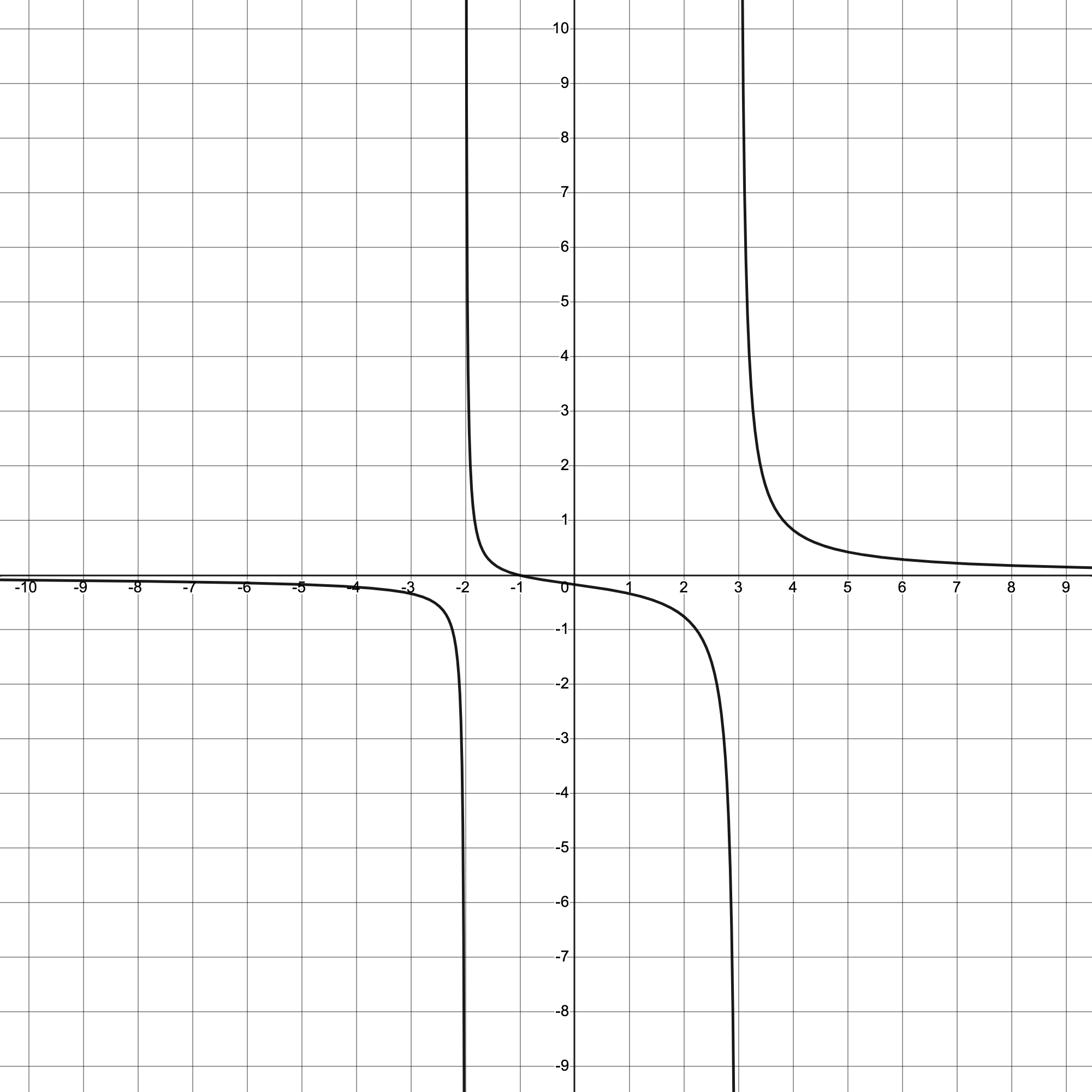
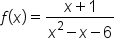
|
Set denominator equal to zero |
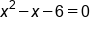
|
Factor the quadratic expression |
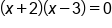
|
Set each factor equal to zero |
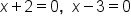
|
Solve each x in each factor |
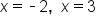
|
Our solutions |
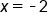 and
and 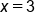 drawn in as dashed vertical lines.
drawn in as dashed vertical lines.
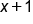 , plug in
, plug in 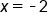 and
and 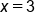 .
.
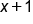
|
Plug in 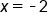
|
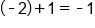
|
Plug in 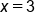
|
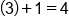
|
Both result in a non-zero numerator |
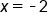 and
and 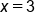 .
.
Another type of asymptote is a horizontal asymptote, which is a horizontal line that a curve approaches from above or below. To find horizontal asymptotes of a rational function, we must analyze the degrees of the polynomials in the numerator and denominator of the fraction.
In general, we can say:
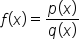
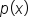 is
is 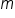 .
.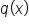 is
is 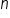 .
.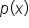 and
and 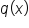 can help us determine the equation to horizontal asymptotes:
can help us determine the equation to horizontal asymptotes:
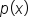 is less than the degree of
is less than the degree of 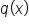 , in other words, if
, in other words, if 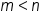 , then the horizontal asymptote is the line
, then the horizontal asymptote is the line 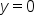 .
.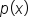 and
and 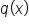 have the same degree, in other words, if
have the same degree, in other words, if 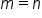 , then the horizontal asymptote is the line
, then the horizontal asymptote is the line 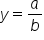 , where a and b are the leading coefficients of the polynomials (we'll get to this later).
, where a and b are the leading coefficients of the polynomials (we'll get to this later). EXAMPLE
Let's consider the previous rational function, as it also has a horizontal asymptote. The equation, once again, is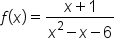 .
.
 , and the degree of the denominator is 2 because there is an
, and the degree of the denominator is 2 because there is an 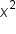 . Since the numerator has a smaller degree, the horizontal asymptote is the line
. Since the numerator has a smaller degree, the horizontal asymptote is the line 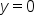 . Here is the graph of the equation once more:
. Here is the graph of the equation once more:
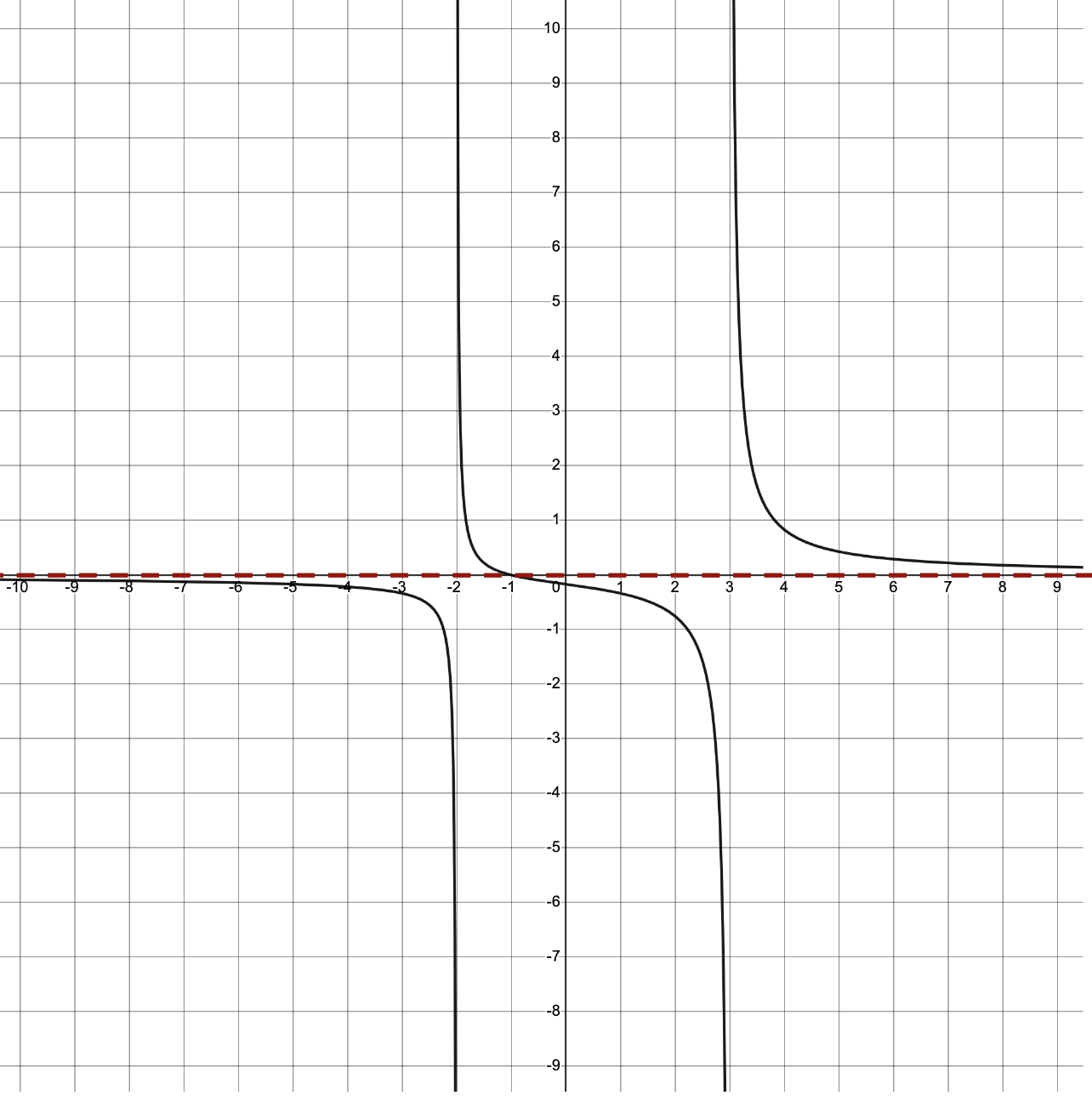
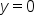 , or the x-axis of the graph, is the horizontal asymptote: the curve tends towards this horizontal line as x approaches positive and negative infinity.
, or the x-axis of the graph, is the horizontal asymptote: the curve tends towards this horizontal line as x approaches positive and negative infinity.
Next, let's consider the case where the degrees are equal. In this case, the horizontal asymptote is found by dividing the leading coefficients of the polynomials. The leading coefficient is the coefficient of the highest degree term in the polynomial.
EXAMPLE
Consider the function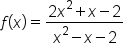 .
.
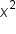 , so they are both second-degree polynomials. This means that we divide the leading coefficients to find the horizontal asymptote. The leading coefficients are 2 (from the
, so they are both second-degree polynomials. This means that we divide the leading coefficients to find the horizontal asymptote. The leading coefficients are 2 (from the 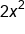 in the numerator) and 1 (from the
in the numerator) and 1 (from the 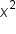 in the denominator). Therefore, the horizontal asymptote is the line
in the denominator). Therefore, the horizontal asymptote is the line 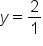 , which is just
, which is just 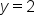 .
.
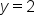 as the horizontal asymptote.
as the horizontal asymptote.
With horizontal asymptotes, we considered either when the degrees of the polynomials in the numerator and denominator are equal, or if the degree in the denominator is greater. If the degree in the numerator is one greater, then the rational function has an oblique (or slant) asymptote. When this happens, the equation for the oblique asymptote is 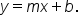
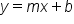 . If the degree in the numerator is greater by more than one degree, the equation for the oblique asymptote will not be linear.
. If the degree in the numerator is greater by more than one degree, the equation for the oblique asymptote will not be linear.
EXAMPLE
Consider the function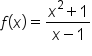 .
.
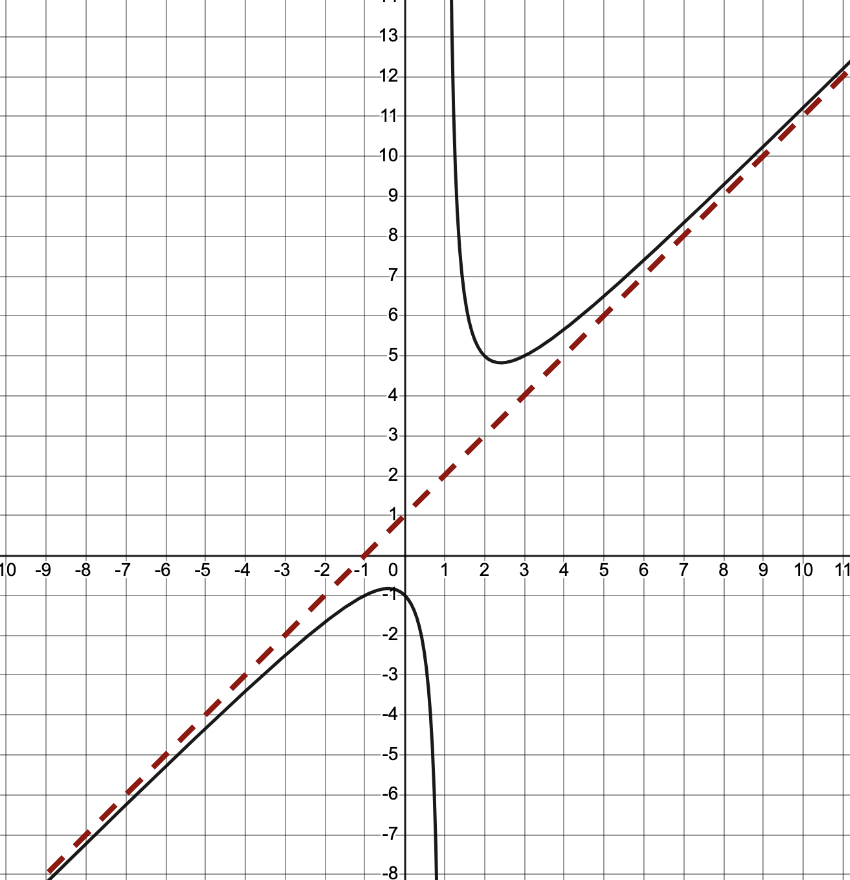
When the degree of the numerator is at least 2 higher than the degree of the denominator, for example in 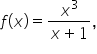 there is no horizontal asymptote nor oblique asymptote; we simply call it a nonlinear asymptote. These are not discussed in this course.
there is no horizontal asymptote nor oblique asymptote; we simply call it a nonlinear asymptote. These are not discussed in this course.
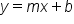 , where
, where 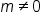 .
.Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License