Table of Contents |
Notice that the exponential equation 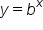 can be written in the form of
can be written in the form of 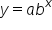 , if
, if 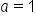 or
or 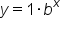 . If the base is a positive number greater than 1, then the general form of the graph will look like this:
. If the base is a positive number greater than 1, then the general form of the graph will look like this:
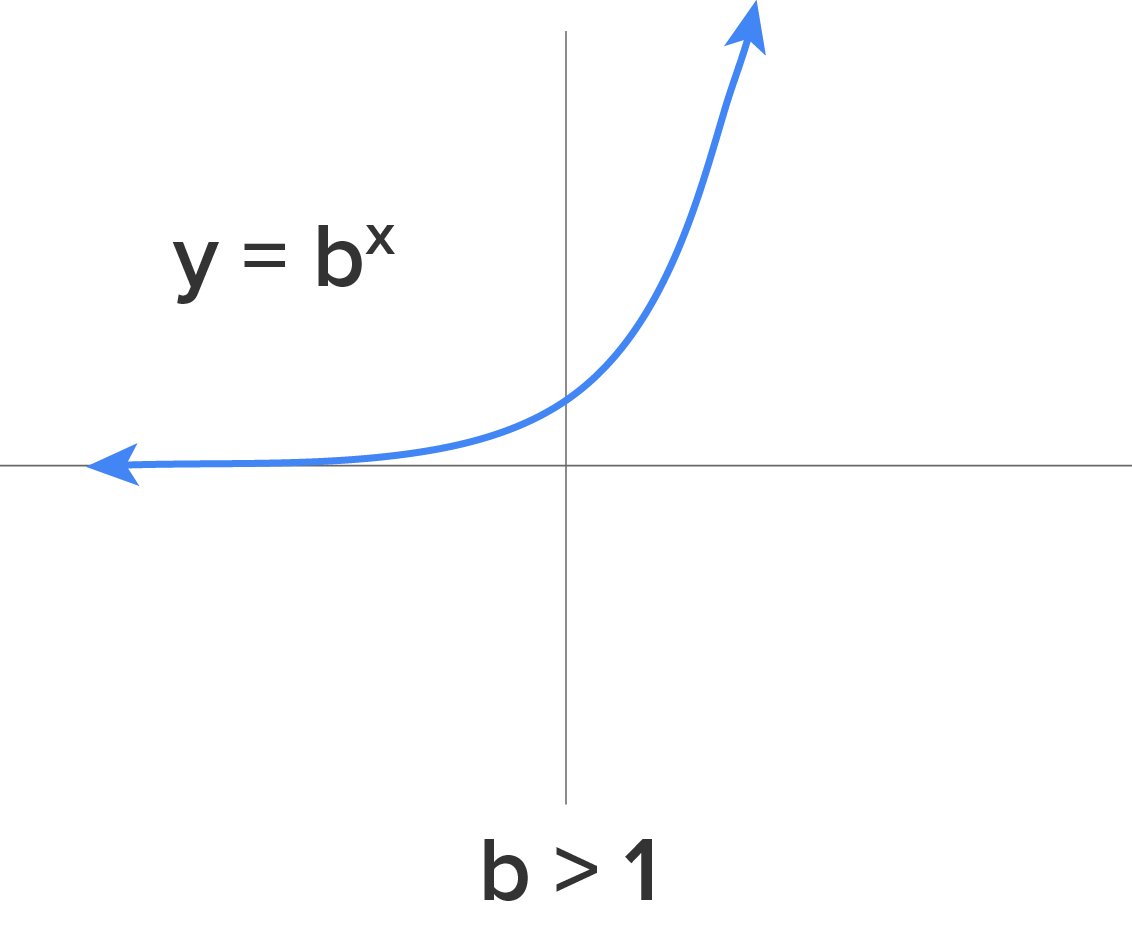
We see that, in this case, as x gets larger (approaches positive infinity), the value of y also increases and approaches positive infinity. The larger the base, b, the faster that y increases to positive infinity. On the other hand, as x gets smaller (approaches negative infinity), the value of y gets smaller as well, but it approaches zero, rather than negative infinity. Again, there are restrictions to the base of exponential equations, such that the base must be greater than 0 and cannot equal 1.
Looking at the graph of the exponential function, the domain of 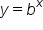 , or the values that x can take on in the equation, are all x values from negative infinity to positive infinity.
, or the values that x can take on in the equation, are all x values from negative infinity to positive infinity.
However, the range, or the y values that will output from the equation, is greater than zero to positive infinity. As the x value approaches negative infinity, the y values approach 0 but never actually touch the x-axis. There are no x values that make y a negative number (when both 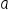 and b are both positive). The range of an exponential function is greater than zero to positive infinity.
and b are both positive). The range of an exponential function is greater than zero to positive infinity.
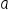 and b are positive:
and b are positive:
We can plot points on an exponential graph by evaluating the function at different values of x. The evaluated y can be put into our coordinate point (x, y). For example, if we evaluate the function 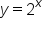 at
at 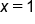 , then we will get
, then we will get 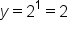 . So, when
. So, when 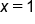 , the evaluated y from the function is 2, or
, the evaluated y from the function is 2, or 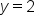 . This means that the point (1, 2) is on the graph of the function
. This means that the point (1, 2) is on the graph of the function 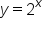 .
.
What is the y-intercept of equations in the form 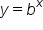 ? Recall, the y-intercept of an equation is the point on the graph at which the line or curve touches or crosses the y-axis. This always occurs when
? Recall, the y-intercept of an equation is the point on the graph at which the line or curve touches or crosses the y-axis. This always occurs when 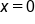 . Let's return to the equation
. Let's return to the equation 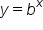 . When x equals 0 or
. When x equals 0 or 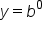 , the y evaluates to 1 because any base number raised to a power of zero is 1 when using the zero property of exponents.
, the y evaluates to 1 because any base number raised to a power of zero is 1 when using the zero property of exponents.
This holds true for all forms of the exponential equation 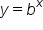 , such as
, such as 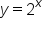 or
or 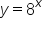 . The y-intercept for these equations evaluates to (0, 1).
. The y-intercept for these equations evaluates to (0, 1).
What is the y-intercept of equations in the form 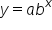 ? Let’s substitute
? Let’s substitute 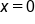 into the general equation.
into the general equation.
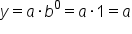
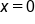 , then
, then 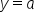 . So, the y-intercept of the exponential equation of the form
. So, the y-intercept of the exponential equation of the form 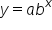 is at the point (0,
is at the point (0, 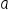 ), because
), because 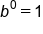 . We can deduce that the y-intercept depends on the value of
. We can deduce that the y-intercept depends on the value of 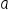 in this case. For the general exponential equation
in this case. For the general exponential equation 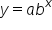 , the y-intercept has the coordinates (0,
, the y-intercept has the coordinates (0, 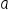 ).
).
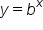 , the y-intercept has coordinates (0, 1) because
, the y-intercept has coordinates (0, 1) because 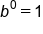 for any accepted base. For equations in the form
for any accepted base. For equations in the form 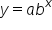 , the y-intercept has coordinates (0,
, the y-intercept has coordinates (0, 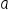 ), for the same reasons above. Notice
), for the same reasons above. Notice 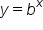 is the specific case when
is the specific case when 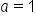 .
.
Now that we can evaluate exponential functions, we can use this to plot points on a graph to visualize the exponential graphs. We already know that the y-intercept of the exponential equation is (0, 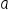 ).
).
EXAMPLE
Graph the function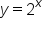 .
.
| x | y = 2x | (x, y) |
|---|---|---|
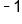
|
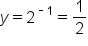
|
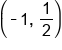
|
|
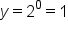
|
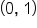
|
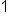
|
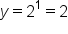
|
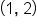
|
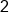
|
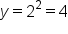
|
|
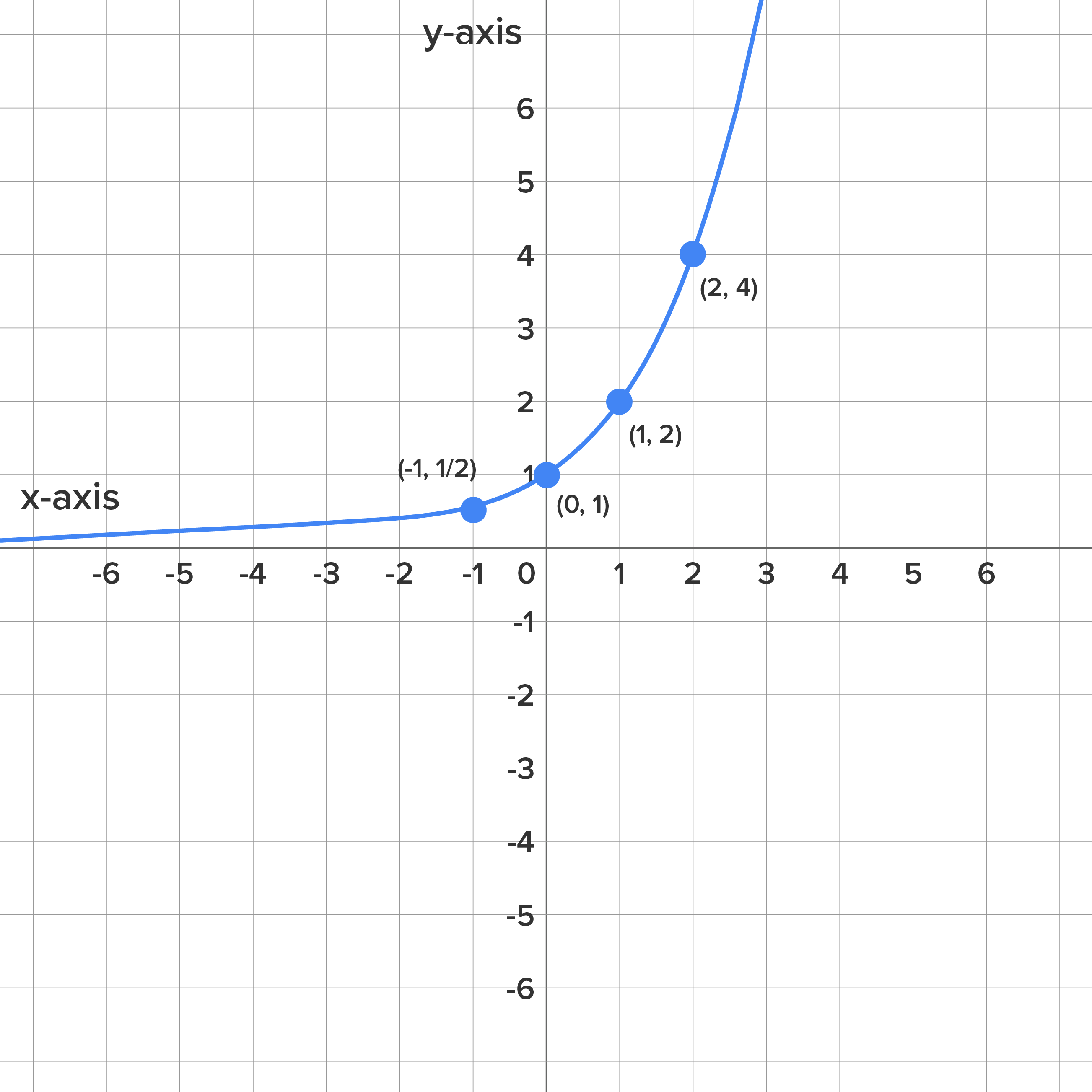
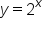 graph.
graph.
EXAMPLE
Graph the function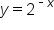 .
.
| x | y = 2x | (x, y) |
|---|---|---|
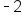
|
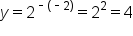
|
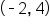
|
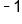
|
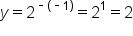
|
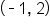
|
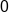
|
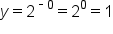
|
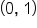
|
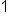
|
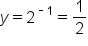
|
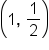
|
|
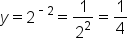
|
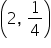
|
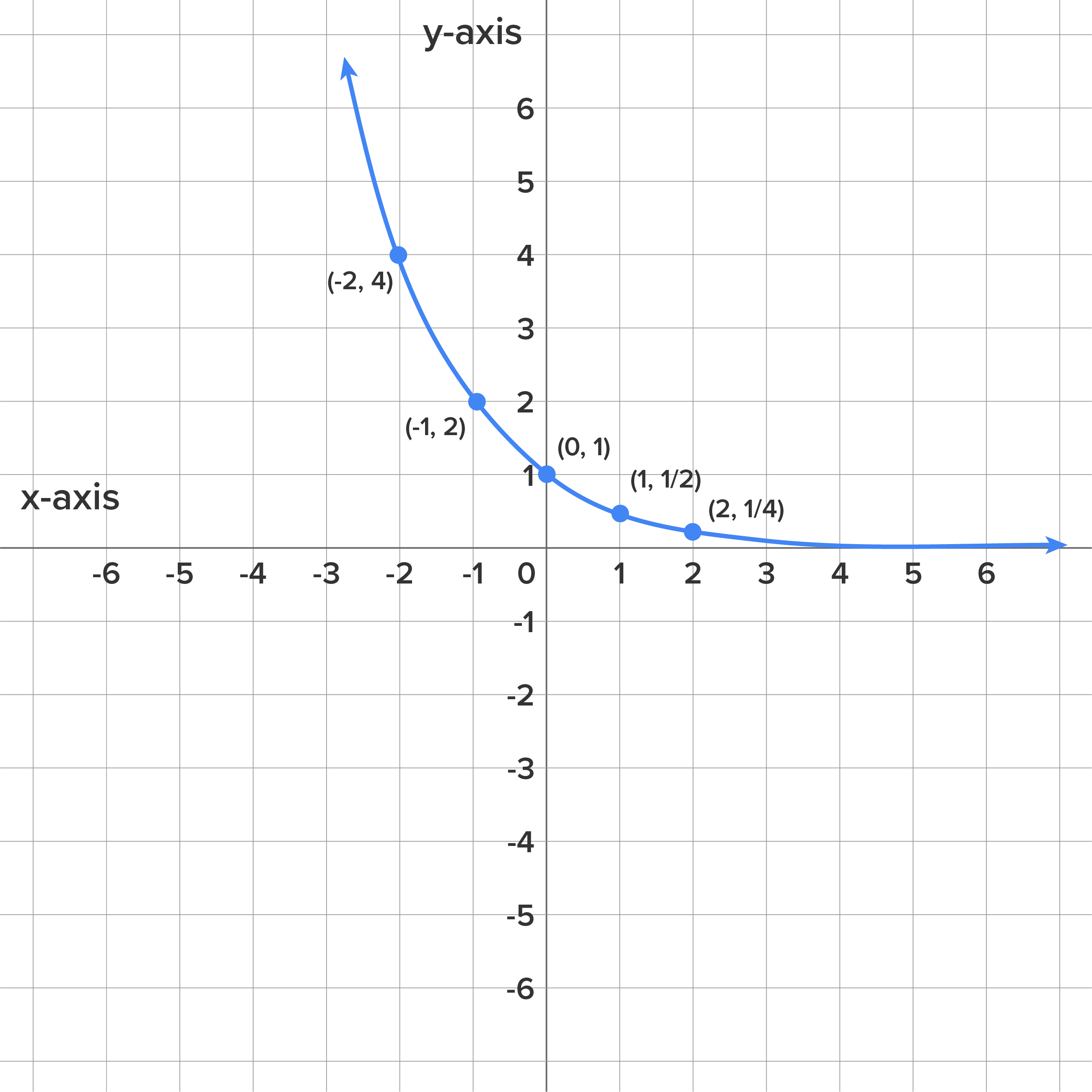
If we compare the graphs of 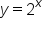 and
and 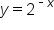 , we can see that it is the same graph reflected over the y-axis. Both graphs have the same y-intercept (0, 1). But,
, we can see that it is the same graph reflected over the y-axis. Both graphs have the same y-intercept (0, 1). But, 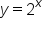 approaches positive infinity as x approaches positive infinity and approaches zero as x approaches negative infinity. For
approaches positive infinity as x approaches positive infinity and approaches zero as x approaches negative infinity. For 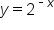 , it is the opposite. As x approaches positive infinity,
, it is the opposite. As x approaches positive infinity, 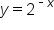 approaches zero, and increases toward positive infinity as x approaches negative infinity.
approaches zero, and increases toward positive infinity as x approaches negative infinity.
As we saw with the graphs of 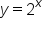 and
and 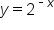 , a negative sign in the exponent can reflect the graph over the y-axis. If a and b are both positive, the graphs will generally look like:
, a negative sign in the exponent can reflect the graph over the y-axis. If a and b are both positive, the graphs will generally look like:
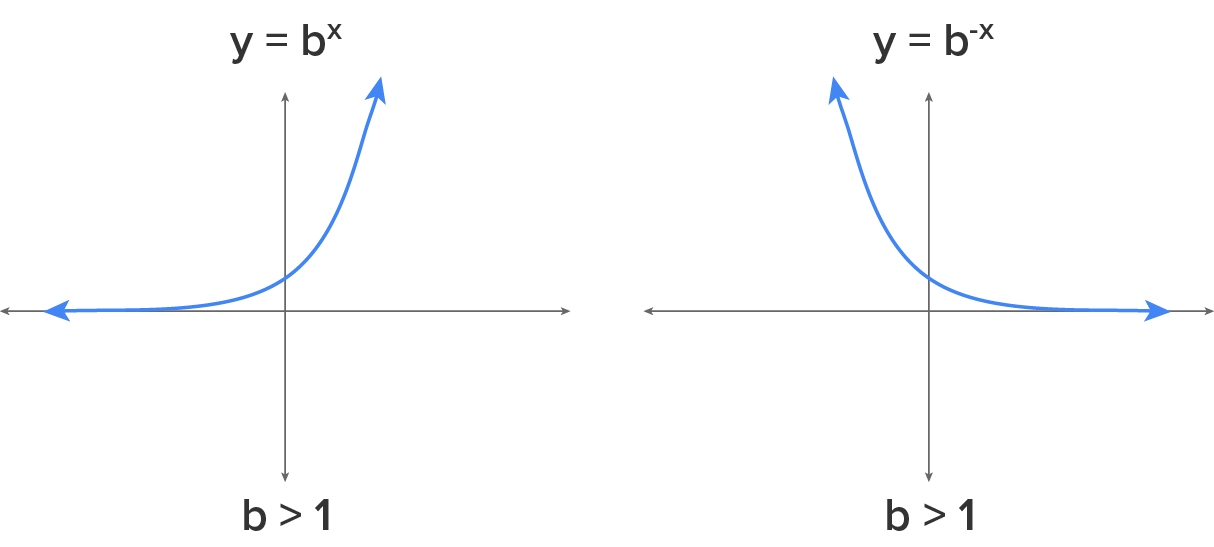
What happens to the graphs when 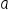 is negative? If we reverse the signs of
is negative? If we reverse the signs of 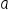 , we end up with different variations of the general exponential curve. The graph will reflect over the x-axis. If we look at the specific example of
, we end up with different variations of the general exponential curve. The graph will reflect over the x-axis. If we look at the specific example of 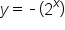 , the y-intercept for this function is (0, -1) according to the property of the exponential function. Below are the general graphs of the exponential functions when
, the y-intercept for this function is (0, -1) according to the property of the exponential function. Below are the general graphs of the exponential functions when 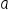 is negative. These patterns are illustrated in the graphs below:
is negative. These patterns are illustrated in the graphs below:
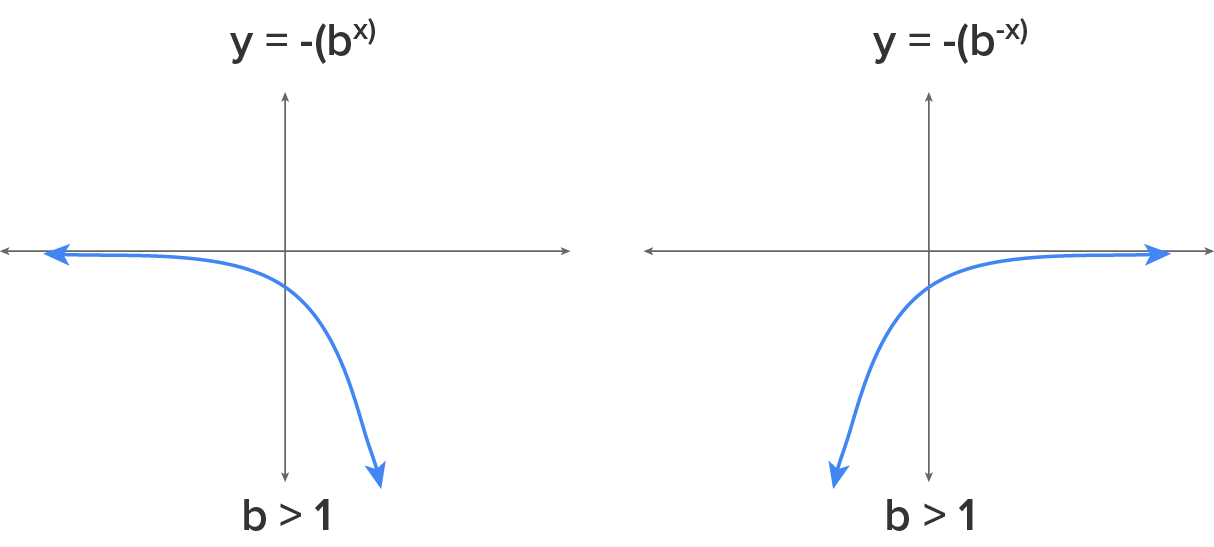
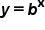 , noting that this exponential equation can be written in the form of
, noting that this exponential equation can be written in the form of 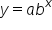 , if
, if 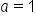 or
or 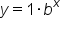 . As x gets larger (approaches positive infinity), the value of y also increases and approaches positive infinity; on the other hand, as x gets smaller (approaches negative infinity), the value of y gets smaller as well, but it approaches zero, rather than negative infinity. You examined the domain and range of
. As x gets larger (approaches positive infinity), the value of y also increases and approaches positive infinity; on the other hand, as x gets smaller (approaches negative infinity), the value of y gets smaller as well, but it approaches zero, rather than negative infinity. You examined the domain and range of 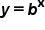 , noting that for exponential functions where
, noting that for exponential functions where 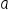 and b are positive, the domain is all x values and the range is restricted to y values greater than zero. You learned that the y-intercept of an exponential equation in the form
and b are positive, the domain is all x values and the range is restricted to y values greater than zero. You learned that the y-intercept of an exponential equation in the form 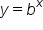 has coordinates (0, 1) because
has coordinates (0, 1) because 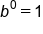 for any accepted base. For equations in the form
for any accepted base. For equations in the form 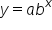 , the y-intercept has coordinates (0,
, the y-intercept has coordinates (0, 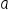 ). You practiced graphing exponential equations by selecting several values of x to evaluate in the function and plotting the points on the graph. Lastly, you learned about other features of the graph
). You practiced graphing exponential equations by selecting several values of x to evaluate in the function and plotting the points on the graph. Lastly, you learned about other features of the graph 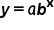 , such as when
, such as when 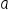 is negative and when the exponent is negative. A negative exponent reflects the graph over the y-axis, while a negative
is negative and when the exponent is negative. A negative exponent reflects the graph over the y-axis, while a negative 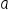 coefficient reflects the graph over the x-axis.
coefficient reflects the graph over the x-axis.Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.