Table of Contents |
To learn more about the graph of the equation 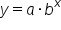 , let's look at a specific case.
, let's look at a specific case.
EXAMPLE
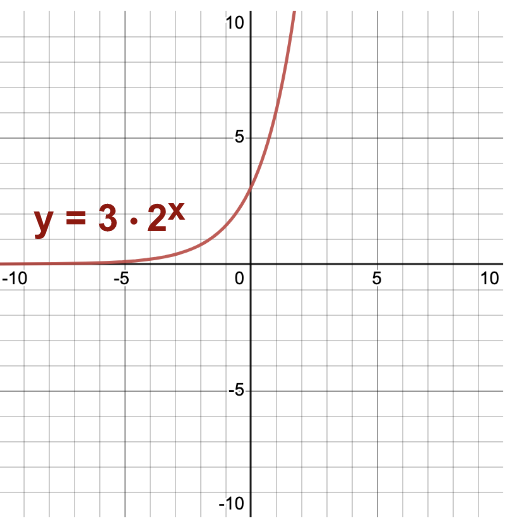
Below is a sketch of the graph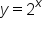 . Notice that the base b to the exponential expression is 2, and there is an implied scalar multiplier of 1 in front of this expression, which would be the a in the equation:
. Notice that the base b to the exponential expression is 2, and there is an implied scalar multiplier of 1 in front of this expression, which would be the a in the equation:
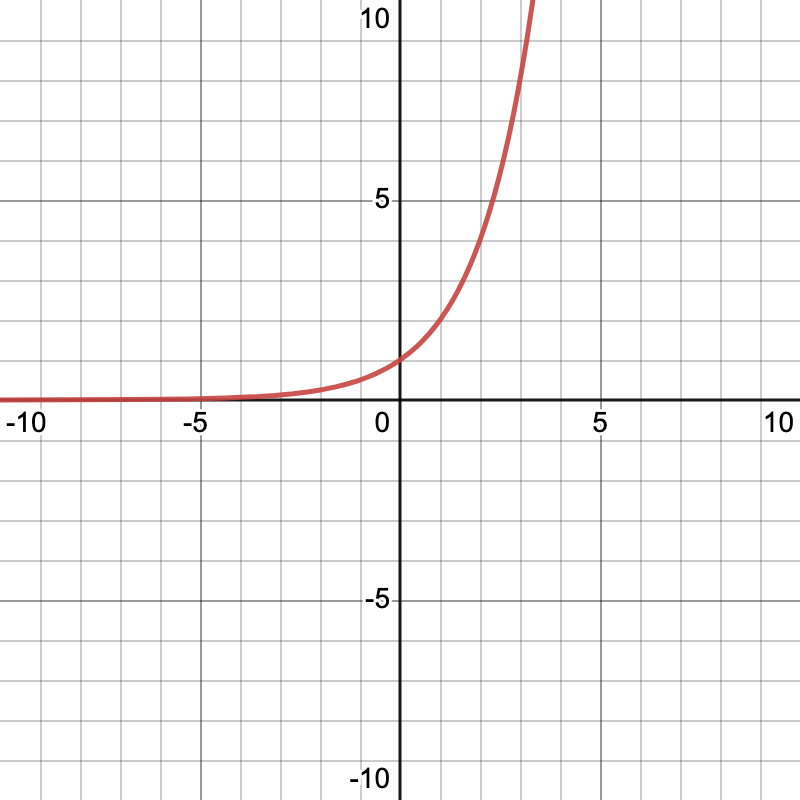
This behavior is characteristic of exponential functions with a base larger than 1. If the base was between 0 and 1, then the behavior would be much different: y would tend towards zero as x gets larger, but tend toward infinity as x gets smaller.
EXAMPLE
Consider the graph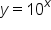 .
.
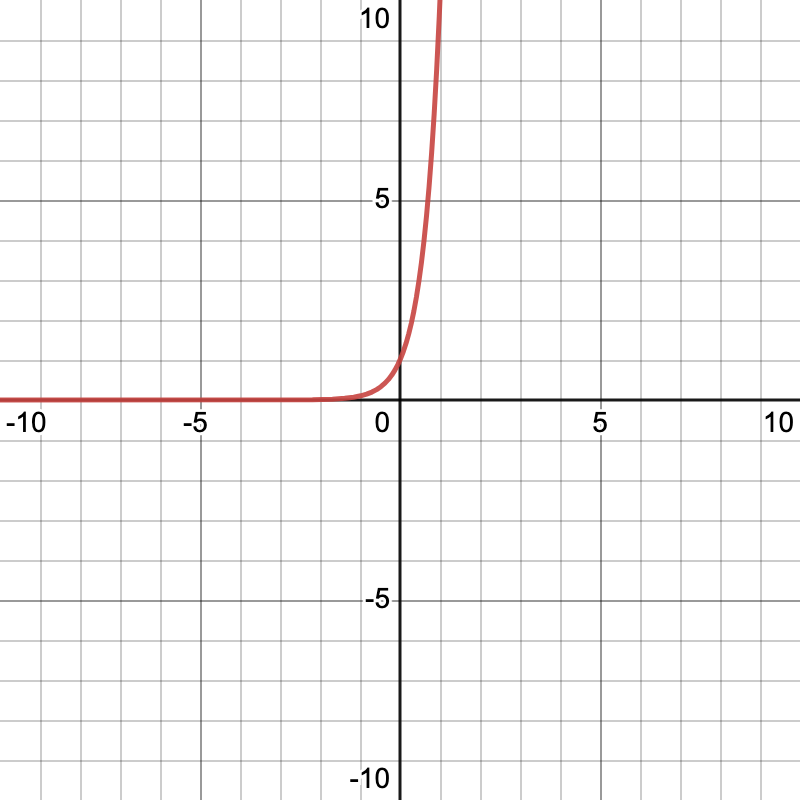
The y-intercept to any equation is the point on the graph at which the line or curve touches or crosses the y-axis. This always occurs when 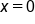 .
.
EXAMPLE
Let's return to the equation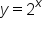 . When x equals 0, y evaluates to 1, because any base number raised to a power of zero is 1. So we can say when x equals 0,
. When x equals 0, y evaluates to 1, because any base number raised to a power of zero is 1. So we can say when x equals 0, 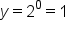 . That must mean this also holds true for the equation
. That must mean this also holds true for the equation 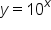 from the second example above.
from the second example above.
For the equation 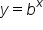 , the y-intercept is at the point (0, 1) because when x equals 0, y equals 1.
, the y-intercept is at the point (0, 1) because when x equals 0, y equals 1.
But what about the y-intercept of equations in the form 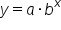 ? We already know that
? We already know that 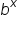 evaluates to 1 when x equals 0 for any base. We can deduce that the y-intercept depends on the value of
evaluates to 1 when x equals 0 for any base. We can deduce that the y-intercept depends on the value of  in this case.
in this case.
For the general exponential equation 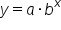 , the y-intercept has the coordinates
, the y-intercept has the coordinates 
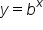 , the y-intercept has coordinates (0, 1).
, the y-intercept has coordinates (0, 1).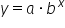 , the y-intercept has coordinates
, the y-intercept has coordinates 
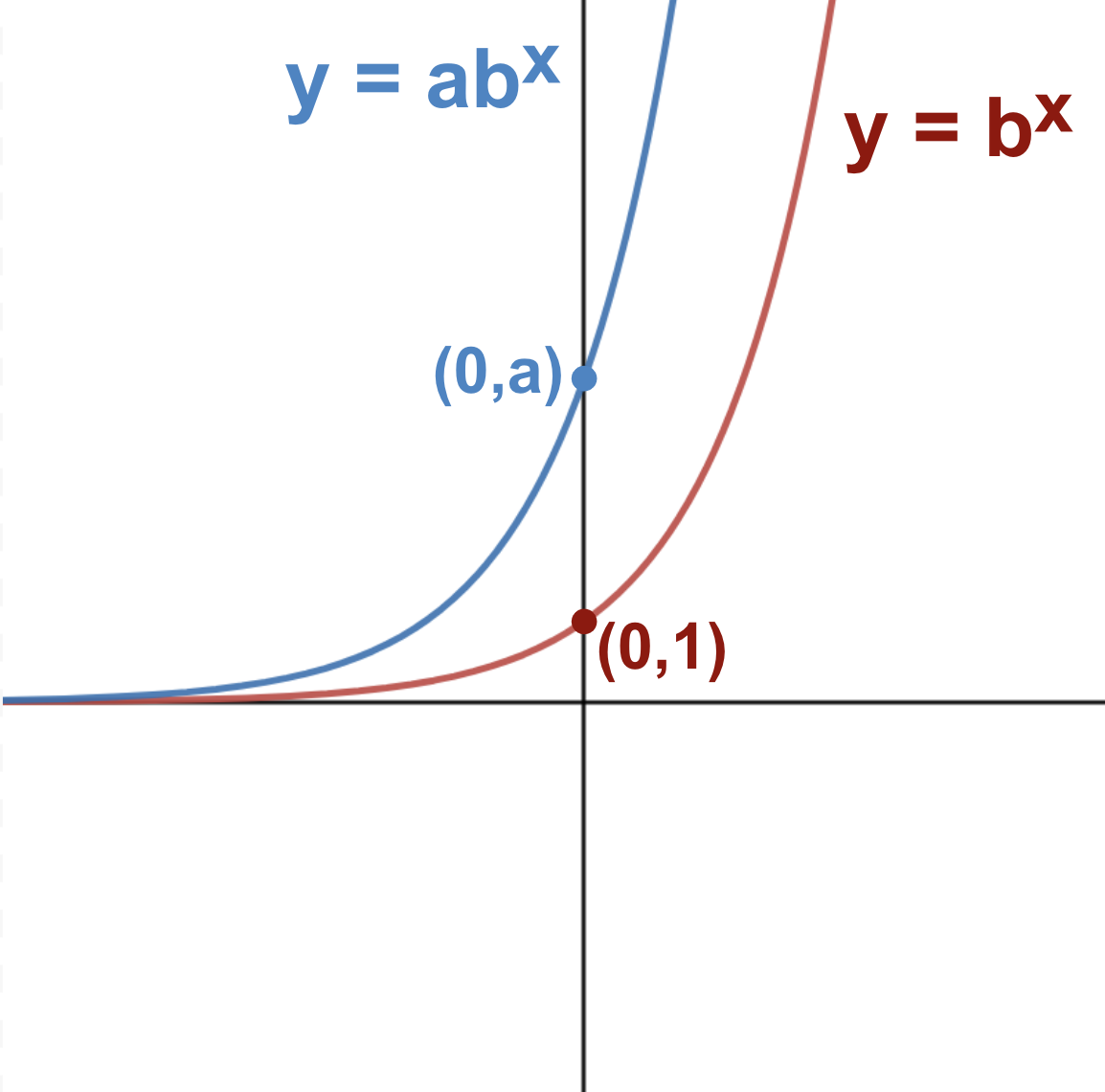
The general exponential equation 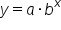 has a positive
has a positive  and a positive x. If we reverse the signs of
and a positive x. If we reverse the signs of  and x in the general exponential equation, we end up with different variations of the general exponential curve. More specifically, these are reflections about either the x- or y-axes or perhaps both, if the signs of both
and x in the general exponential equation, we end up with different variations of the general exponential curve. More specifically, these are reflections about either the x- or y-axes or perhaps both, if the signs of both  and x are reversed. These patterns are illustrated in the graphs below:
and x are reversed. These patterns are illustrated in the graphs below:
Let's look at the characteristics of each case.
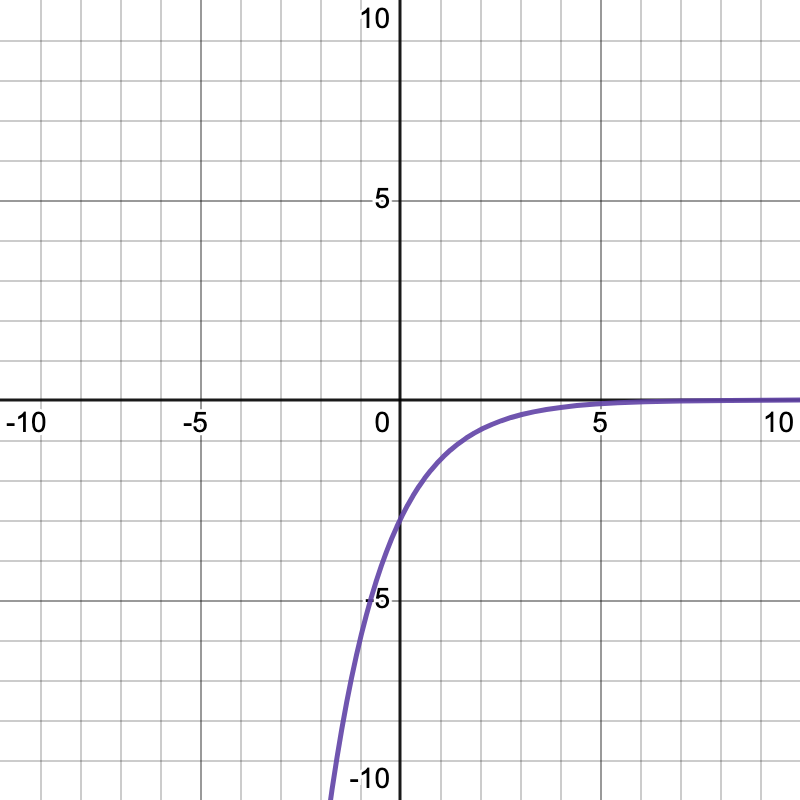
Having a positive  and a positive exponent is the general exponential equation:
and a positive exponent is the general exponential equation:
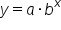
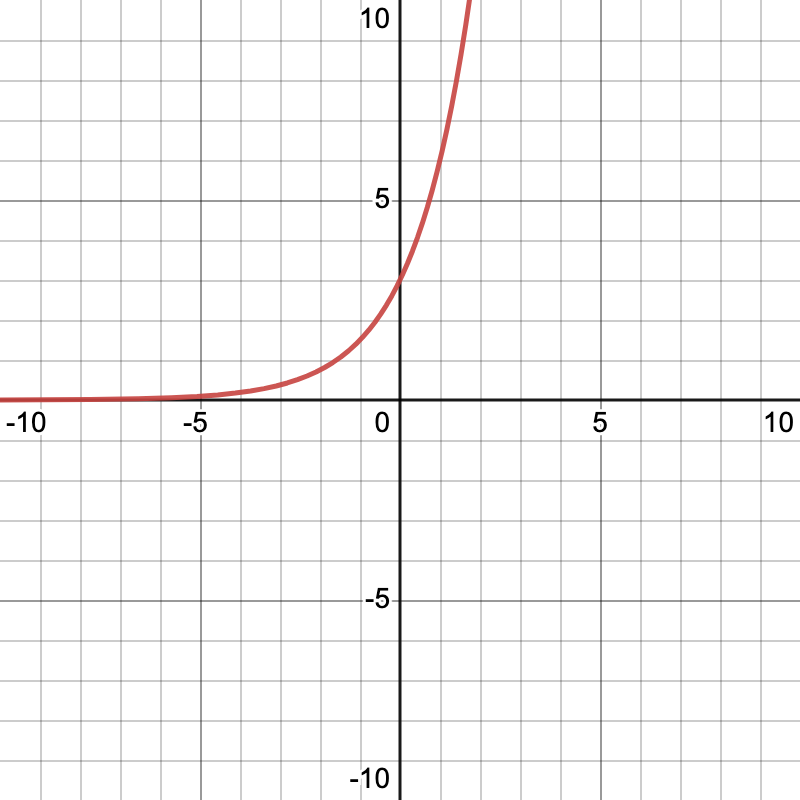
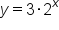 . In this graph, as x is tending toward positive infinity, y goes to positive infinity, and as x goes to negative infinity, y approaches 0.
. In this graph, as x is tending toward positive infinity, y goes to positive infinity, and as x goes to negative infinity, y approaches 0.
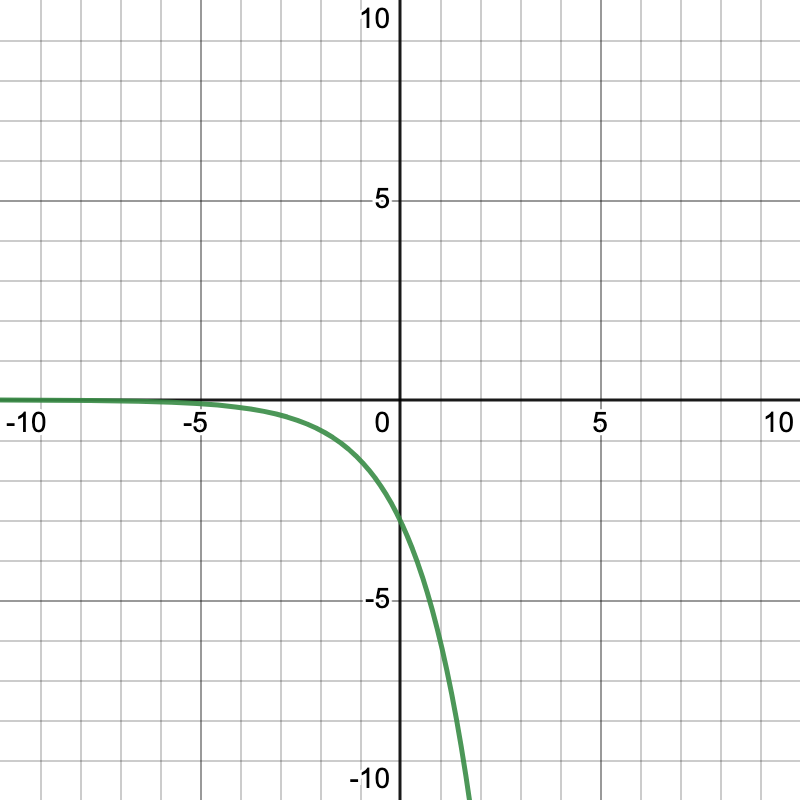
Let's take a further look into the next comparison of having a positive or negative exponent, but still having a positive 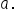
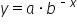
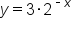 . A similar equation to
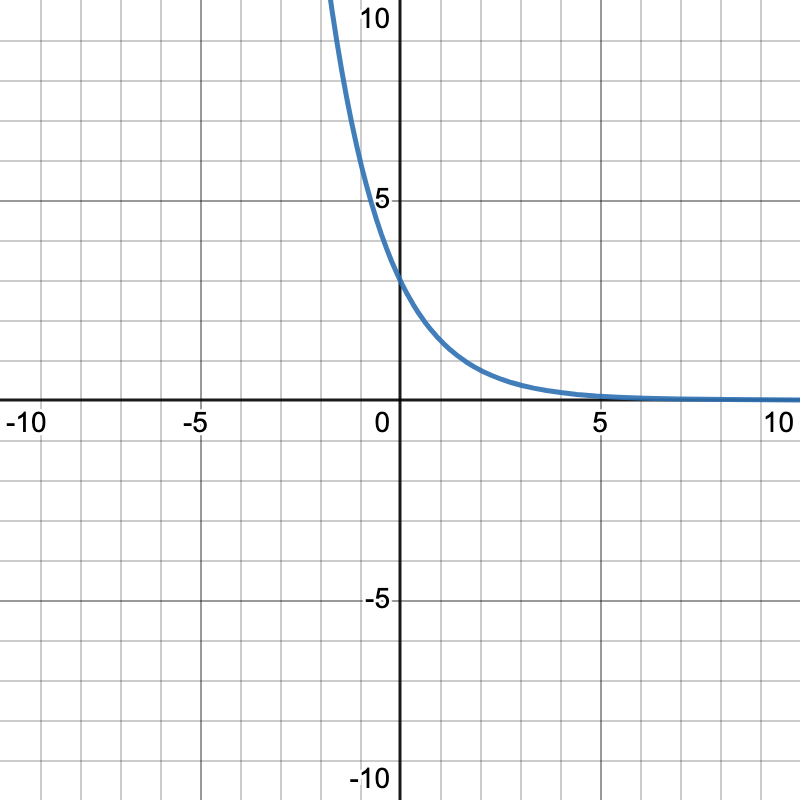
. A similar equation to 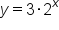 , but this equation has a negative exponent. We can see that since negative x and positive x are opposite, their graphs have opposite effects. When our exponent is negative, as x approaches positive infinity, now y is approaching 0, and as x is approaching negative infinity, then our y is approaching positive infinity.
, but this equation has a negative exponent. We can see that since negative x and positive x are opposite, their graphs have opposite effects. When our exponent is negative, as x approaches positive infinity, now y is approaching 0, and as x is approaching negative infinity, then our y is approaching positive infinity.
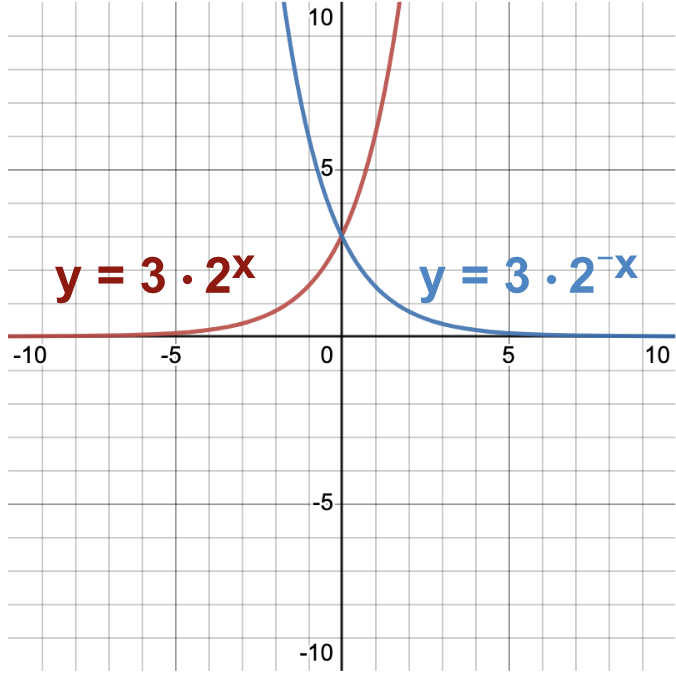
The next characteristic we'll look at is comparing the equations and graphs of exponential equations when the value of 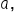 the number in front of the base, is positive or negative.
the number in front of the base, is positive or negative.
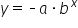
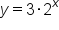 . Let's compare that to the equation and graph of
. Let's compare that to the equation and graph of 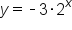 . In the graphs, we can see that it looks like the graph is reflected over the x-axis. When the
. In the graphs, we can see that it looks like the graph is reflected over the x-axis. When the  value is negative, as the x-values approach positive infinity, the y-values approach negative infinity. It's decreasing instead of increasing. Also, notice that as the x-values approach negative infinity, the y-values are still approaching 0 as they were with a graph of our equation with a positive
value is negative, as the x-values approach positive infinity, the y-values approach negative infinity. It's decreasing instead of increasing. Also, notice that as the x-values approach negative infinity, the y-values are still approaching 0 as they were with a graph of our equation with a positive  value.
value.
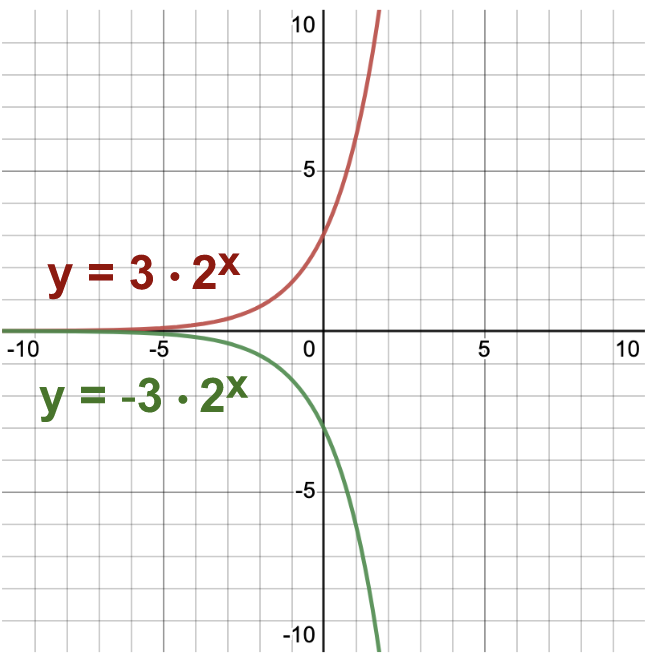
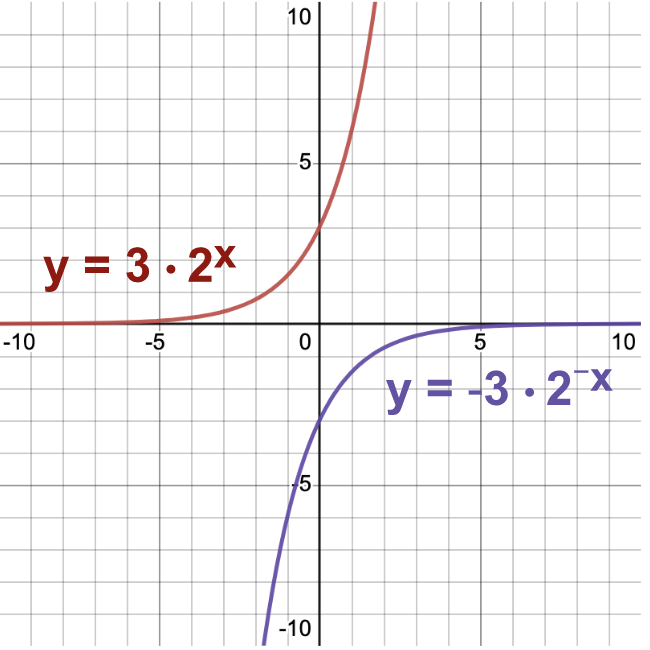
Finally let's look at the characteristics of exponential equations that have both a negative  value and a negative exponent.
value and a negative exponent.
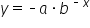
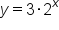 and
and 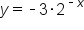 . This second equation has both a negative
. This second equation has both a negative  value and a negative exponent. When the equation has a negative
value and a negative exponent. When the equation has a negative  and negative exponent, as the x-values approach positive infinity, we see that the y-values approach 0, and as the x-values approach negative infinity, we see that the y-values are also approaching negative infinity.
and negative exponent, as the x-values approach positive infinity, we see that the y-values approach 0, and as the x-values approach negative infinity, we see that the y-values are also approaching negative infinity.
|
|
|---|---|
|
|
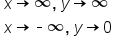
|
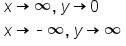
|
|
|
|
|
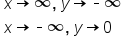
|
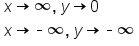
|
 is an exponential equation. The graph of
is an exponential equation. The graph of 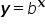 has certain characteristics. The y-intercept of the
has certain characteristics. The y-intercept of the 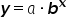 function is equal to the value of
function is equal to the value of  in the equation. Other features of the graph include looking at cases when
in the equation. Other features of the graph include looking at cases when  is negative and when the exponent is negative. A negative exponent reflects the graph over the y-axis. while a negative
is negative and when the exponent is negative. A negative exponent reflects the graph over the y-axis. while a negative  coefficient reflects the graph over the x-axis.
coefficient reflects the graph over the x-axis.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License