Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Graph of a Logarithmic Function

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn to identify features of a logarithmic graph. Specifically, this lesson will cover:

Table of Contents

1. Graph of Exponential; Functions vs. Logarithmic Functions

Exponents and logarithms are inverse operations. This means that as functions, they are inverses of each other. There is a special relationship between inverse functions on a graph: the line 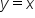y equals x is a line of symmetry or reflection between a function and its inverse. So, we should expect this relationship to hold true when examining the graphs of an exponential function and a logarithmic function:

EXAMPLE

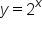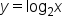The functions y equals 2 to the power of x and y equals log subscript 2 x are inverses. In the table below you see some key points that are on each graph.

x bold italic y bold equals bold 2 to the power of bold x Point x bold italic y bold equals bold log subscript bold 2 bold italic x Point
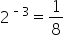
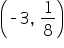
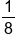
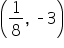
-3 2 to the power of short dash 3 end exponent equals 1 over 8 open parentheses short dash 3 comma space 1 over 8 close parentheses 1 over 8 log subscript 2 open parentheses 1 over 8 close parentheses equals short dash 3 open parentheses 1 over 8 comma space short dash 3 close parentheses
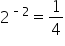
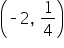
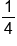
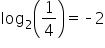
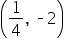
-2 2 to the power of short dash 2 end exponent equals 1 fourth open parentheses short dash 2 comma space 1 fourth close parentheses 1 fourth log subscript 2 open parentheses 1 fourth close parentheses equals short dash 2 open parentheses 1 fourth comma space short dash 2 close parentheses
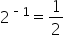
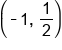
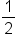
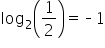
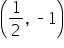
-1 2 to the power of short dash 1 end exponent equals 1 half open parentheses short dash 1 comma space 1 half close parentheses 1 half log subscript 2 open parentheses 1 half close parentheses equals short dash 1 open parentheses 1 half comma space short dash 1 close parentheses
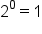
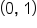
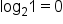
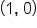
0 2 to the power of 0 equals 1 open parentheses 0 comma space 1 close parentheses 1 log subscript 2 1 equals 0 open parentheses 1 comma space 0 close parentheses
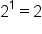
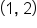
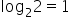
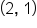
1 2 to the power of 1 equals 2 open parentheses 1 comma space 2 close parentheses 2 log subscript 2 2 equals 1 open parentheses 2 comma space 1 close parentheses
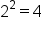
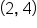
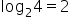
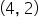
2 2 squared equals 4 open parentheses 2 comma space 4 close parentheses 4 log subscript 2 4 equals 2 open parentheses 4 comma space 2 close parentheses
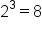
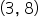
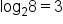
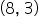
3 2 cubed equals 8 open parentheses 3 comma space 8 close parentheses 8 log subscript 2 8 equals 3 open parentheses 8 comma space 3 close parentheses

The graphs of each are below.



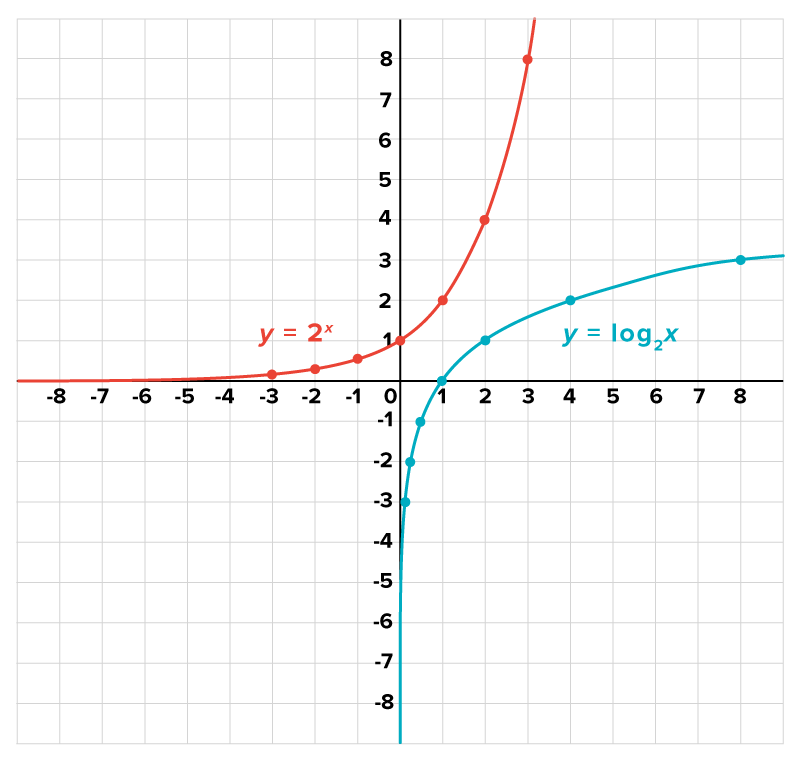
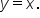Note how the graphs together have symmetry with the line y equals x. This is visual evidence that they are inverses. This is what the graph of a logarithmic function looks like. We’ll get into more details in the coming material.

2. Domain and Range of Logarithmic Functions

As we can see in the graph above, since a function is symmetrical to its inverse about the line 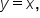y equals x comma we can interchange x- and y-values to plot points on a function's inverse. This also means that the domain and range of a function switches as we describe the domain and range of its inverse. That is, the domain of a function becomes the range of its inverse, and the range of a function becomes the domain of its inverse.

Looking at the graph of the exponential function, we can see that the domain is all real x-values, written 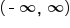open parentheses short dash infinity comma space infinity close parentheses in interval notation. This means that the range of logarithmic functions is all real y-values, written open parentheses short dash infinity comma space infinity close parentheses.

However, when looking at the range of the general exponential function graphed above, we see that the range is 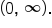open parentheses 0 comma space infinity close parentheses. As the x-values approach negative infinity, the y-values approach 0 but never actually touch the x-axis. Also, there are no x values that make y negative (at least in this case). So, the range of an exponential function is positive y-values written 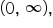open parentheses 0 comma space infinity close parentheses comma which means the domain of the logarithmic function is restricted to positive x-values, written 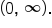open parentheses 0 comma space infinity close parentheses. Inputting a negative value (or zero) into the logarithmic function will yield a non-real answer.

hint
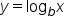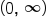The logarithmic function y equals log subscript b x has domain open parentheses 0 comma space infinity close parentheses and range open parentheses short dash infinity comma space infinity close parentheses.

We can use this idea to find domain and range of logarithmic functions that have inputs other than x.

EXAMPLE

Find the domain and range of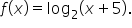 f open parentheses x close parentheses equals log subscript 2 open parentheses x plus 5 close parentheses.

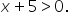Domain: We need to make sure that we are applying the logarithm to a positive number. This means that x plus 5 greater than 0. If we solve this inequality, we have 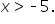x greater than short dash 5. Using interval notation, this is written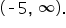 open parentheses short dash 5 comma space infinity close parentheses.

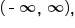Range: Since the range of any logarithmic function is the set of all real numbers, the range of this function is also open parentheses short dash infinity comma space infinity close parentheses comma written using interval notation. 

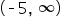In conclusion, the domain is open parentheses short dash 5 comma space infinity close parentheses and the range is open parentheses short dash infinity comma space infinity close parentheses.

try it
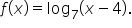
Consider the function f open parentheses x close parentheses equals log subscript 7 open parentheses x minus 4 close parentheses.
What is the domain of the function? 
Set x minus 4 greater than 0 and solve. The result is open parentheses 4 comma space infinity close parentheses.
What is the range of the function? 
The range of a logarithmic function is all real numbers. In interval notation, we can say that the range of this function is open parentheses short dash infinity comma space infinity close parentheses.

3. Finding the x-intercept of a Logarithmic Function

Earlier, we looked at the graph of 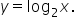y equals log subscript 2 x. Note that the graph passed through the point 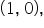open parentheses 1 comma space 0 close parentheses comma making this the graph’s x-intercept.

In general, for any base b, the graph of 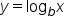y equals log subscript b x has its x-intercept at the point 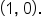open parentheses 1 comma space 0 close parentheses. This is because 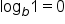log subscript b 1 equals 0 for any positive base b (except 1).

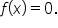Recall that in general, the graph of y equals f open parentheses x close parentheses has x-intercept when f open parentheses x close parentheses equals 0. That is, we replace f open parentheses x close parentheses with 0, then solve for x.

EXAMPLE

Find the x-intercept of the graph of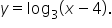 y equals log subscript 3 open parentheses x minus 4 close parentheses.

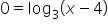
0 equals log subscript 3 open parentheses x minus 4 close parentheses Replace y with 0.
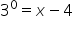
3 to the power of 0 equals x minus 4 Rewrite the equation in exponential form.
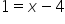
1 equals x minus 4 Simplify 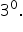3 to the power of 0.
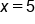
x equals 5 Add 4 to both sides to solve for x.

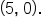
Therefore, the x-intercept is open parentheses 5 comma space 0 close parentheses.

4. Finding the Vertical Asymptote of a Logarithmic Function

Recall that the graph of an exponential function 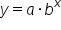y equals a times b to the power of x has a horizontal asymptote at 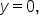y equals 0 comma meaning that the graph approaches this line in the long run (but never touches it).

Since the logarithmic function is the inverse of the exponential function, it stands to reason that the function 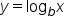y equals log subscript b x has a vertical asymptote at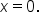 x equals 0.

Note that the location of the vertical asymptote corresponds to the value of x where the input of the logarithmic function is also 0.

EXAMPLE

Find the equation of the vertical asymptote of the function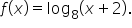 f open parentheses x close parentheses equals log subscript 8 open parentheses x plus 2 close parentheses.

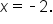The vertical asymptote corresponds to the value of x where x plus 2 equals 0 comma or x equals short dash 2. Therefore, the equation of the vertical asymptote is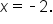 x equals short dash 2.

The graph of f open parentheses x close parentheses is shown below, with the vertical asymptote drawn as a dashed line.

try it
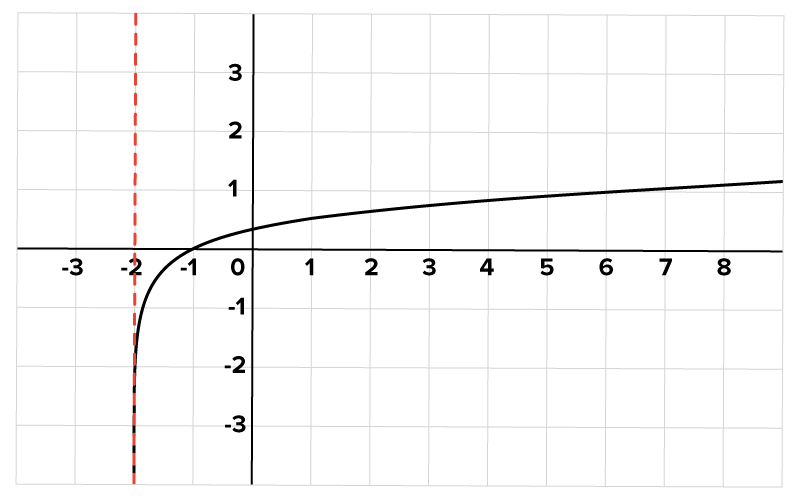
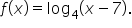
Consider the function f open parentheses x close parentheses equals log subscript 4 open parentheses x minus 7 close parentheses.
Find the x-intercept of the graph of f  (x  ).
Solving log subscript 4 open parentheses x minus 7 close parentheses equals 0 comma you would get x equals 8. The x-intercept is open parentheses 8 comma space 0 close parentheses.
Write the equation of the vertical asymptote of the graph of f  (x  ).
Setting x minus 7 equals 0 comma we have x equals 7. This is the equation of the vertical asymptote. 

Notice that the graph of a logarithmic function appears to “level off” as x rightwards arrow infinity. This is not the case though since we know that the range of a logarithmic function is all real numbers. In other words, it may appear that a logarithmic function has a horizontal asymptote, but it doesn’t.

summary
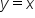When comparing the graph of exponential functions versus the graph of logarithmic functions, the graph of an exponential function reflected over the line y equals x is the graph of a logarithmic function. This is because exponential and logarithmic functions are inverses of each other. The domain of a logarithmic function is the set of all values of x for which the input to the logarithm is positive whole the range of a logarithmic function is the set of all real numbers. The x-intercept of a logarithmic function is the value of x for which the logarithm is equal to 0. The vertical asymptote of a logarithmic function is found by setting the input equal to 0, then solving for x. Even though it is visually deceiving, the graph of a logarithmic function has no horizontal asymptote.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.