Table of Contents |
In the previous example, notice that each term is twice its previous term.
This is an example of a geometric sequence. A geometric sequence is a sequence in which every term after the first term is obtained by multiplying some constant to the previous term. This constant is called the common ratio, which is denoted r.
The sequence 5, 10, 20, 40, 80, … from above has common ratio 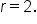 When taking any two consecutive terms and dividing the second by the first, the ratio is equal to the common ratio.
When taking any two consecutive terms and dividing the second by the first, the ratio is equal to the common ratio.
There are two ways to determine if a sequence is geometric:
EXAMPLE
Consider the sequence 2, -6, 18, -54, ….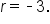
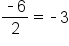
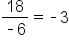
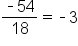
EXAMPLE
Consider the sequence 2, 6, 12, 36, 108, ….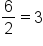 , but
, but 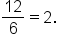 There is no common ratio.
There is no common ratio.
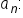
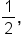
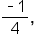
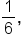
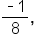 ...
...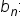 27, 18, 12, 8, ...
27, 18, 12, 8, ... 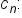 1, -1, 1, -1, …
1, -1, 1, -1, …When given the first term and a common ratio, a geometric sequence is formed by multiplying by the common ratio r to get each subsequent term.
EXAMPLE
A geometric sequence is to have first term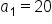 and common ratio
and common ratio 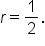 Write the next three terms of the sequence.
Write the next three terms of the sequence.
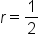 tells us that we multiply each term by
tells us that we multiply each term by 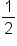 to get the next term.
to get the next term.
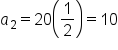
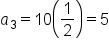
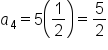
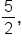 ….
….
A similar idea can be used to relate two terms of an geometric sequence with common ratio r.
EXAMPLE
A geometric sequence has term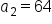 and common ratio
and common ratio 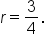

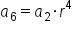
|
Starting at 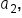 multiply the common ratio 4 times to get the value of multiply the common ratio 4 times to get the value of 
|
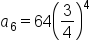
|
Substitute 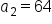 and and 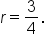
|
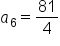
|
Simplify. |
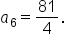
We can also use this strategy to find a missing common ratio if two terms are known.
EXAMPLE
A geometric sequence has terms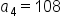 and
and 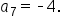 What is the common ratio r, and what is the value of
What is the common ratio r, and what is the value of 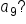
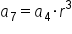
|
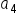 and and 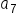 are 3 spaces apart in the sequence; therefore, multiply are 3 spaces apart in the sequence; therefore, multiply 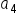 by r three times to get the value of by r three times to get the value of 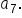
|
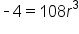
|
Substitute 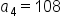 and and 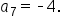
|
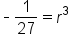
|
Divide both sides by 108. |
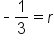
|
Take the cube root of both sides. |
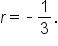
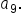
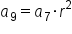
|
Since 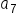 is known, relate it to is known, relate it to 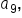 which is 2 spaces after which is 2 spaces after 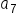 in the sequence. in the sequence.
|
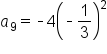
|
Substitute 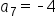 and and 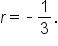
|
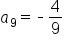
|
Simplify. |
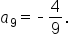
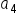 is also known, we could have used the equation
is also known, we could have used the equation 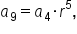 which gives the same results.
which gives the same results.
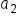 and
and 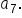
The recursive formula for a geometric sequence with first term 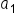 is
is 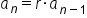 for
for 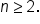
It is also possible to find an explicit formula for the nth term, which is always more desirable.
Suppose a geometric sequence has first term 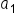 and we wish to find a formula for
and we wish to find a formula for 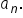
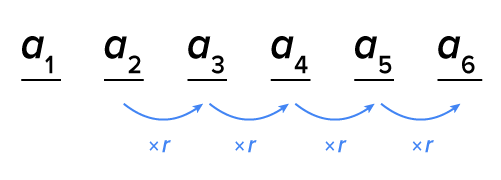
The picture below shows the first six terms of a geometric sequence, and how r is multiplied to get each subsequent term.
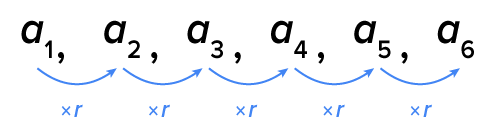
From the sequence, we have the following relationships between 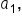 r, and the other terms of the sequence:
r, and the other terms of the sequence:
| Equation | Relationship |
|---|---|
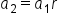
|
Multiply r to 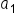 to get the value of to get the value of 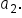
|
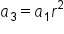
|
Multiply r twice to 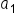 to get the value of to get the value of 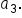
|
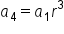
|
Multiply r three times to 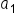 to get the value of to get the value of 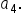
|
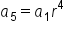
|
Multiply r four times to 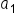 to get the value of to get the value of 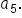
|
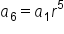
|
Multiply r five times to 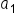 to get the value of to get the value of 
|
This pattern continues.
Notice that the number of times 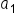 is multiplied by r is one less than the position of the term we seek.
is multiplied by r is one less than the position of the term we seek.
This leads to the following formula, which is the most conventional way to find the nth term of a geometric sequence.
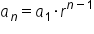
EXAMPLE
Find a formula for the nth term: 400, 440, 484, …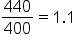 and
and 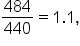 we assume that this sequence is geometric with common ratio
we assume that this sequence is geometric with common ratio 
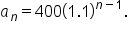
EXAMPLE
Find a formula for the nth term: 27, -18, 12, -8, …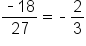
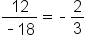
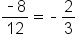
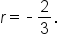
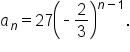
Geometric sequences can be used in applied situations that involve a percent increase or decrease.
EXAMPLE
The starting salary at a new job is $60,000 and is expected to increase by 2% each year.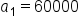 and
and 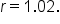
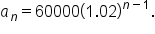
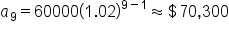 to the nearest whole dollar.
to the nearest whole dollar.
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS