Table of Contents |
The amount of time between the present and future is called the number of periods. A period is a general block of time. Usually, a period is 1 year. The number of periods can be represented as either t or n.
Suppose you are making an investment, such as depositing your money in a bank. If you plan on leaving the money there for 1 year, you’re making a single-period investment.
You can calculate an investment with the following formulas:
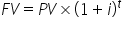
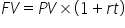
In each equation, the variables are defined as follows:
We will address these formulas later, but note that for a single period of 1 year, when t = 1, both formulas become FV = PV × (1 + i).
Thus, in a single period, there is only one formula you need to know:
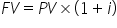
IN CONTEXT
Suppose you deposit $100 into a bank account that pays 3% interest. What is the balance in your account after 1 year?
In this case, your PV is $100 and your interest is 3%. You want to know the value of your investment in the future, so you’re solving for FV. Since this is a single-period investment, t (or n) is 1.
Plugging the numbers into the formula, you get this:
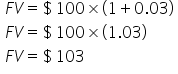
Your balance will be $103 in 1 year.
Multiperiod investments take place over more than one period, usually multiple years. They can accrue either simple or compound interest. There are two primary ways of determining how much an investment will be worth in the future if the time frame is more than one period.
The first concept of accruing or earning interest is called simple interest. With simple interest, you earn interest only on the amount you originally invested, or the principal. Your total balance will go up each period, because you earn interest each period, but the interest is paid only on the amount you originally borrowed/deposited.
Simple interest is expressed through the following formula:
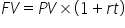
IN CONTEXT
Suppose you make a deposit of $100 in the bank and earn 5% interest per year. After 1 year, you earn 5% interest, or $5, bringing your total balance to $105. One more year passes, and it’s time to accrue more interest. Since simple interest is paid only on your principal ($100), you earn 5% of $100, not 5% of $105. That means you earn another $5 in the second year and will earn $5 for every year of the investment.
The second way of accruing interest is called compound interest. In this case, interest is paid at the end of each period based on the balance in the account. In simple interest, it is only how much the principal is that matters. In compound interest, it is what the balance is that matters. Compound interest is named as such because the interest compounds: Interest is paid on interest.
Compound interest is expressed through the following formula:
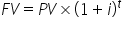
IN CONTEXT
Suppose you make the same $100 deposit into a bank account that pays 5%, but this time, the interest is compounded. After the first year, you will again have $105. At the end of the second year, you also earn 5%, but it’s 5% of your balance, or $105. You earn $5.25 in interest in the second year, bringing your balance to $110.25. In the third year, you earn interest of 5% of your balance, or $110.25. You earn $5.51 in interest, bringing your total to $115.76.
When calculating the future value (FV), you are calculating how much a given amount of money today will be worth some time in the future. In order to calculate the FV, the other three variables (present value, interest rate, and number of periods) must be known.
It is also important to remember that the interest rate and the number of periods must be in the same units. That is, if the interest rate is 5% per year, one period is 1 year. However, if the interest rate is 5% per month, t or n must reflect the number of periods in terms of months.
IN CONTEXT
Example 1: Compound, Yearly Loan, Yearly Interest
What is the FV of a $500, 10-year loan with 7% annual interest?
In this case, the PV is $500, t is 10 years, and i is 7% per year. The next step is to plug these numbers into an equation. But recall that there are two different formulas for the two different types of interest: simple interest and compound interest. If the problem doesn’t specify how the interest is accrued, assume it is compound interest, at least for business problems.
So, using the compound interest formula, we see that the FV is equal to $983.58:
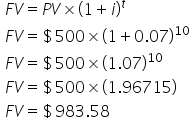
In practical terms, you just calculated how much your loan will be in 10 years. This calculation assumes that you don’t need to make any payments during the 10 years and that the interest compounds. Unless the problem states otherwise, it is safe to make these assumptions—you will be told if there are payments during the 10-year period or if it is simple interest.
IN CONTEXT
Example 2: Compound, Yearly Loan, Monthly Interest
Suppose we want to again find the FV of an $800, 10-year loan but with an interest rate of 1% per month.
Remember that the interest rate and number of periods must be in the same units. In this case, the loan is in units of years, but the interest rate is in units of months. In order to get our total number of periods (t), we multiply 12 months by 10 years, which equals 120 periods.
Therefore, we can see that the FV is equal to $2,640.31:
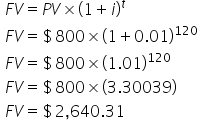
IN CONTEXT
Example 3: Simple, Yearly Loan, Yearly Interest
Suppose you take out a $5,000, 8-year loan, with this one accruing 5% interest per year. The loan accrues interest on the principal only. What is the total FV?
Since the loan is accruing interest on just the principal, this means that we will use the simple interest formula and get an FV of $7,000:
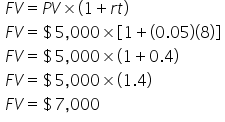
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BOUNDLESS FINANCE" PROVIDED BY LUMEN LEARNING BOUNDLESS COURSES. ACCESS FOR FREE AT LUMEN LEARNING BOUNDLESS COURSES. LICENSED UNDER CREATIVE COMMONS ATTRIBUTION-SHAREALIKE 4.0 INTERNATIONAL.