Fundamental Counting Principle

1. Fundamental Counting Principle

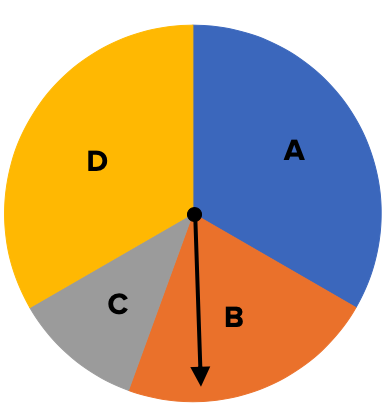
Consider a chance experiment where you roll the die below and spin this spinner.

Each of these spinning sections is not equally likely. But there are, in fact, four sections. How many different outcomes of this experiment are possible?

One way to visualize this is with something we call a tree diagram. To start, we're going to enumerate all the possible outcomes that could happen from the first chance experiment, which is rolling the die. So, we're going to make a tree with six possibilities for the die: 1, 2, 3, 4, 5, and 6.

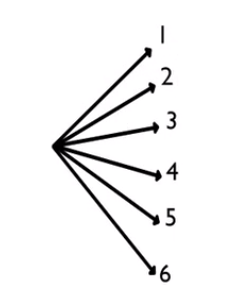
Next in the tree are all the possibilities for the spinner, for each possibility for the die. For instance, if a 1 is rolled, the spinner might spin A, B, C, or D. If a 2 is rolled, the spinner might land on A, B, C, or D, etc. Each outcome represents a different path: One path is 1, C, for example. Another path is 1, D, and so forth. What you end up seeing are 24 different outcomes. There are six branches for the die, each of which has four outcomes for the spinner. So, it's like calculating 6 times 4.

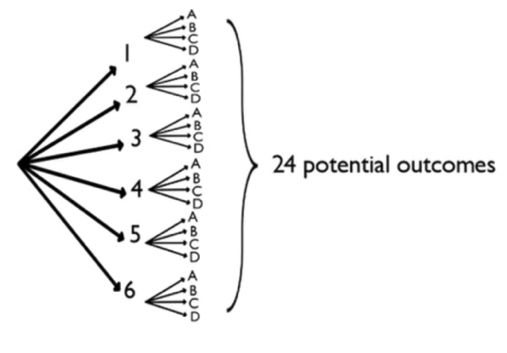
In fact, that's what the fundamental counting principle says. It says if you do two chance experiments, A and B, then experiment A has m potential outcomes, and experiment B has n potential outcomes. It follows, then, that there are m times n potential outcomes when experiments A and B are performed together.

terms to know

Tree Diagram

A way to visualize the different "paths" that a sequence of chance experiments could take.

Fundamental Counting Principle

If chance experiment A has m possible outcomes for one trial, and chance experiment B has n possible outcomes for its trial (independent of the first trial), then there are m times n (m x n) potential outcomes when A and B are done together.

2. Applying the Fundamental Counting Principle

The fundamental counting principle can actually extend beyond just two experiments. It can extend to three, four, five, or however many experiments are being conducted together, by simply multiplying the number of potential outcomes for each consecutive experiment.

think about it

In the example above, there were six outcomes for the die and four outcomes for the spinner, so there were 6 x 4, or 24 potential outcomes. But what if we added another spinner that had three outcomes? How do you think we would find the number of potential outcomes?

Using the definition of the fundamental counting principle, we can apply the following formula to find the number of possible outcomes for independent events to occur together.

formula to know

Fundamental Counting Principle

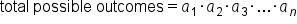
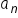where is the number of ways for a specific independent event.

IN CONTEXT

A family is going to have three children. How many different orderings of children are there in terms of boys and girls?

The first child could be a boy or a girl. If you start with a boy, you could have another boy, and the third child could be a girl. Another outcome is that you could have three boys.

If you start with a girl, the second and third child could both be boys. Another outcome could be that you have two girls, then have a boy.

As you can see, there are many different outcomes. To find all possible outcomes, you can create a tree diagram.



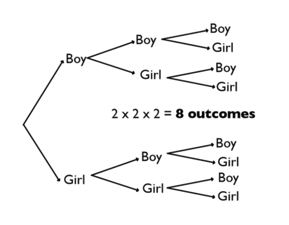
Looking at all the tree diagram branches here, you can see there are eight possible outcomes.

An easier way to do it would be to use the fundamental counting principle. For the first child, there are two options; for the second child, two options; and for the third child, two options.

So, 2 x 2 x 2 = 8 outcomes. The tree diagram isn't really necessary. The number of choices for each of the children multiplied by each outcome for the children is what is needed.