 to sketch the graph of its derivative,
to sketch the graph of its derivative, 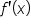 . Specifically, this lesson will cover:
. Specifically, this lesson will cover:
Table of Contents |
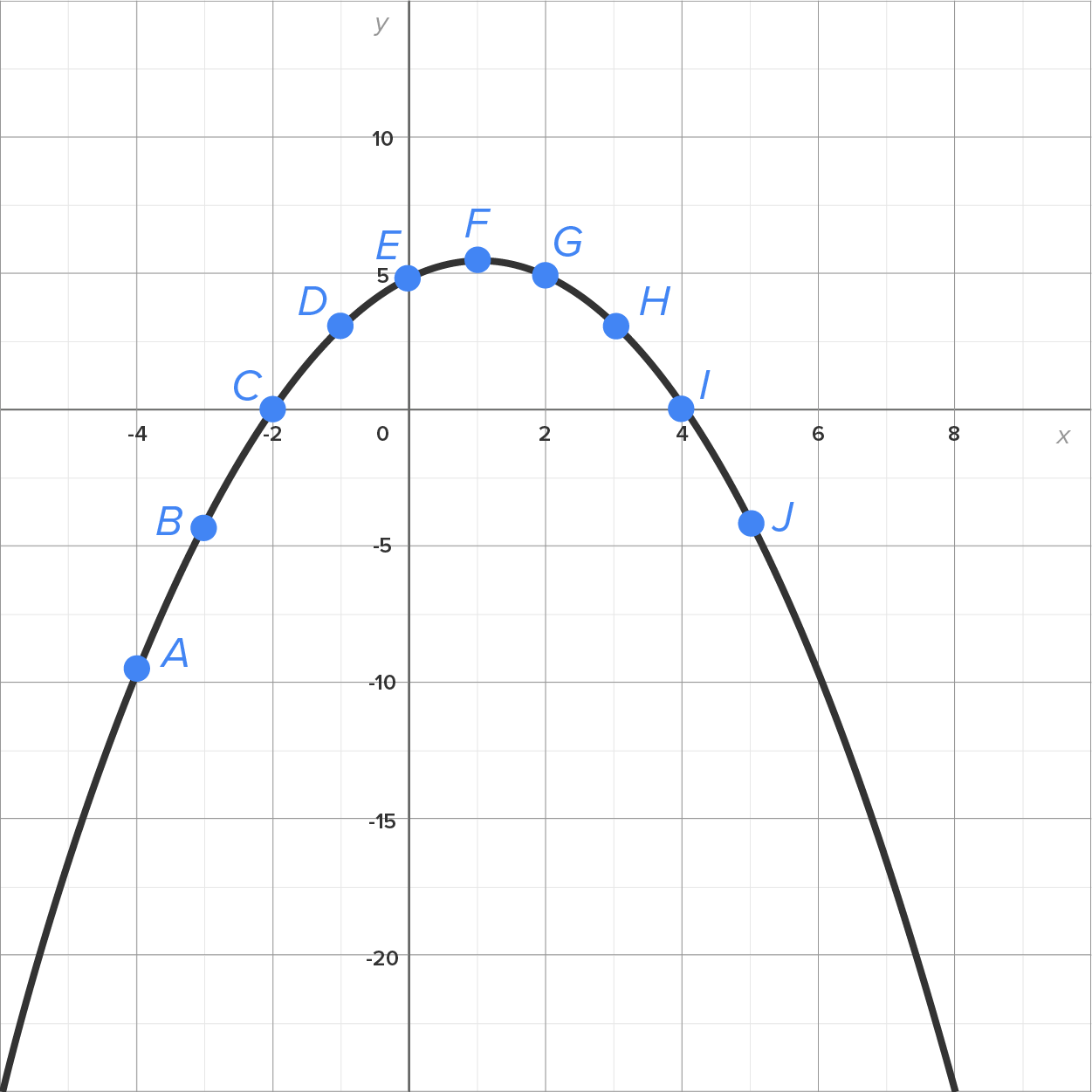
Consider the graph of a function 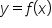 , shown below.
, shown below.
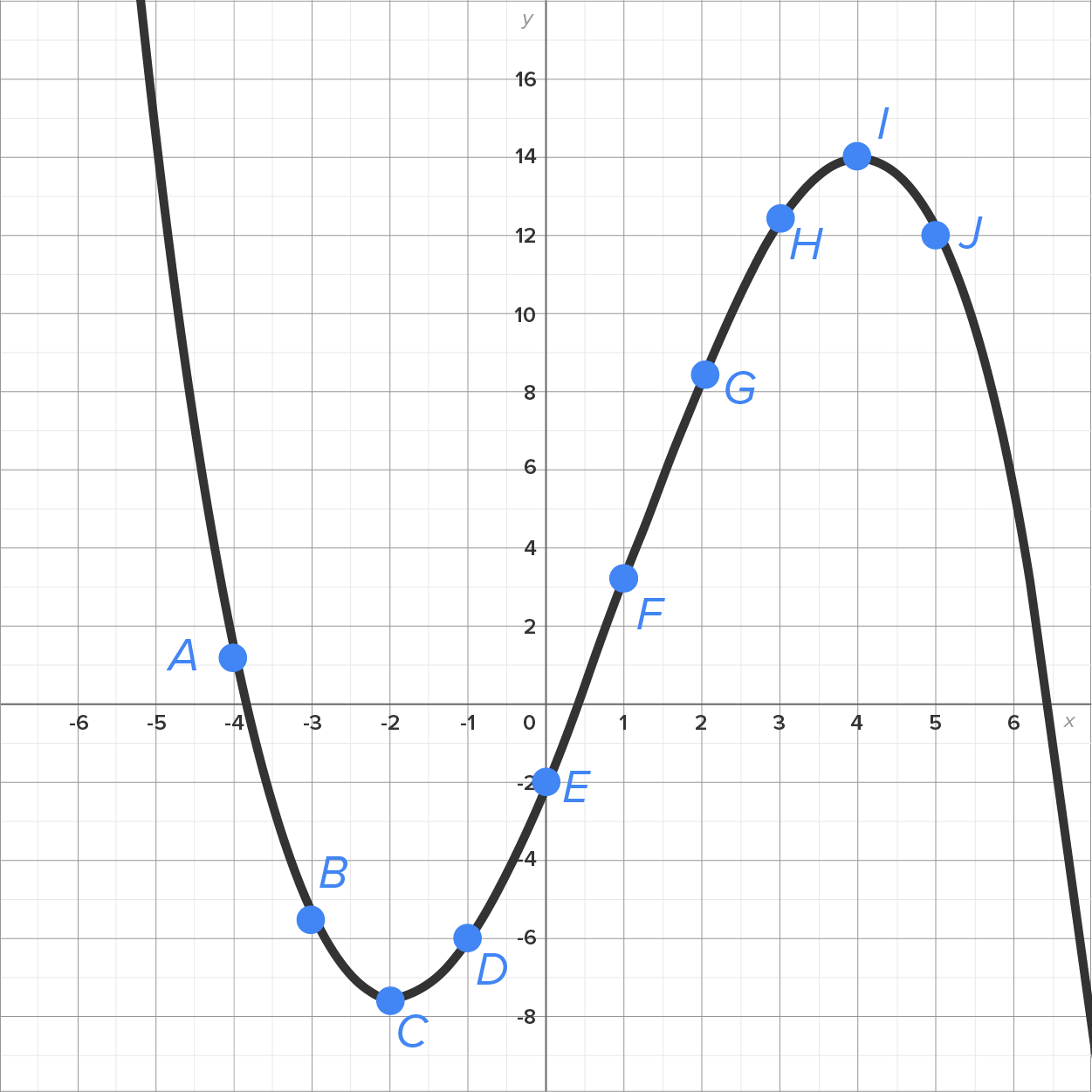
Note that the graph is decreasing at points A, B, and J. Notice also that the slopes of the tangent lines at each of these points are negative.
Note that the graph increases at points D, E, F, G, and H. Notice also that the slopes of the tangent lines at each of these points are positive.
Finally, points C and I are local maximum/minimum points. Notice also that the slope of the tangent line at each of these points is zero.
This leads to a very useful link between the behavior of  and the value of
and the value of 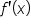 .
.
 is increasing at
is increasing at  , then
, then 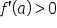 .
.  is decreasing at
is decreasing at  , then
, then 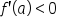 .
.
Given what we know about 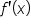 when
when  is increasing or decreasing, we can get a rough sketch of the graph of
is increasing or decreasing, we can get a rough sketch of the graph of 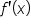 when given the graph of
when given the graph of  .
.
EXAMPLE
Consider the graph of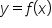 shown below with tangent line segments at points A through J. Notice also the local minimum at point C and the local maximum at point I.
shown below with tangent line segments at points A through J. Notice also the local minimum at point C and the local maximum at point I.
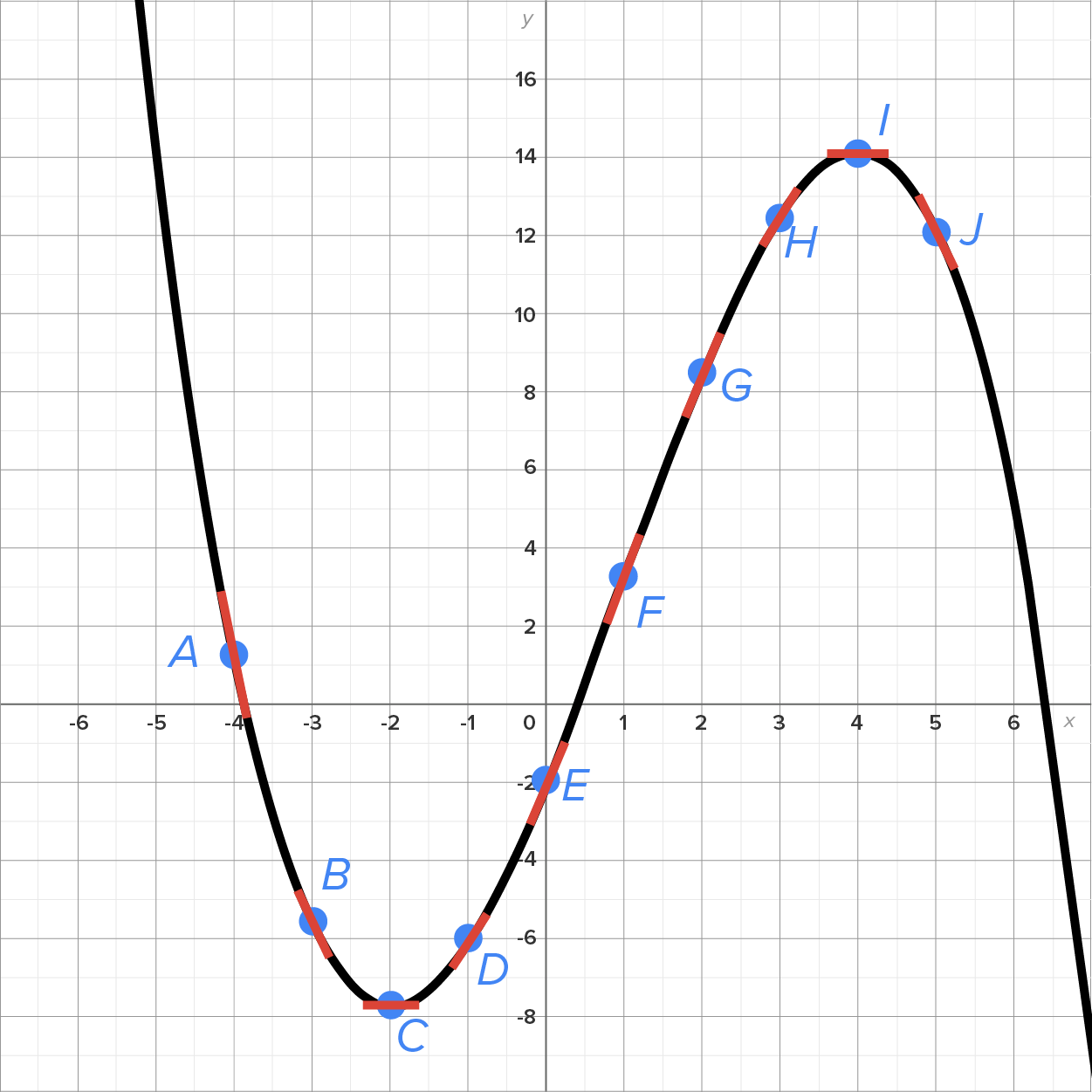
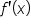 can be summarized in the following table at each point. Remember that
can be summarized in the following table at each point. Remember that 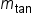 is the value of
is the value of 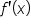 at any point.
at any point.
| Point |
Value of 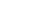
|
|---|---|
| A |
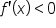
|
| B |
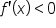 , but the value of , but the value of 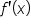 is larger than its value at A is larger than its value at A
|
| C |
 (horizontal tangent line) (horizontal tangent line)
|
| D |
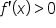
|
| E |
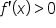 , but its value is noticeably greater than the slope at point D , but its value is noticeably greater than the slope at point D
|
| F |
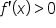 , but its value is slightly greater than the slope at point E , but its value is slightly greater than the slope at point E
|
| G |
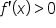 , but its value is slightly less than the slope at point F , but its value is slightly less than the slope at point F
|
| H |
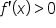 , but its value is noticeably less than the slope at point G , but its value is noticeably less than the slope at point G
|
| I |
 (horizontal tangent line) (horizontal tangent line)
|
| J |
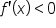
|
 .
.
 and the value of
and the value of 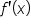 . Specifically, given the graph of
. Specifically, given the graph of 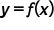 , it is possible to sketch the graph of
, it is possible to sketch the graph of 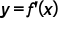 by using slopes of the tangent lines at given points and their respective behavior.
by using slopes of the tangent lines at given points and their respective behavior.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.