Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Finding Maximums and Minimums of a Function

Author: Sophia
PDF Version

what's covered
In this lesson, you will use derivatives and critical numbers to find local maximum and local minimum values. Specifically, this lesson will cover:

Table of Contents

1. The Relationship Between Critical Numbers and Local Extrema

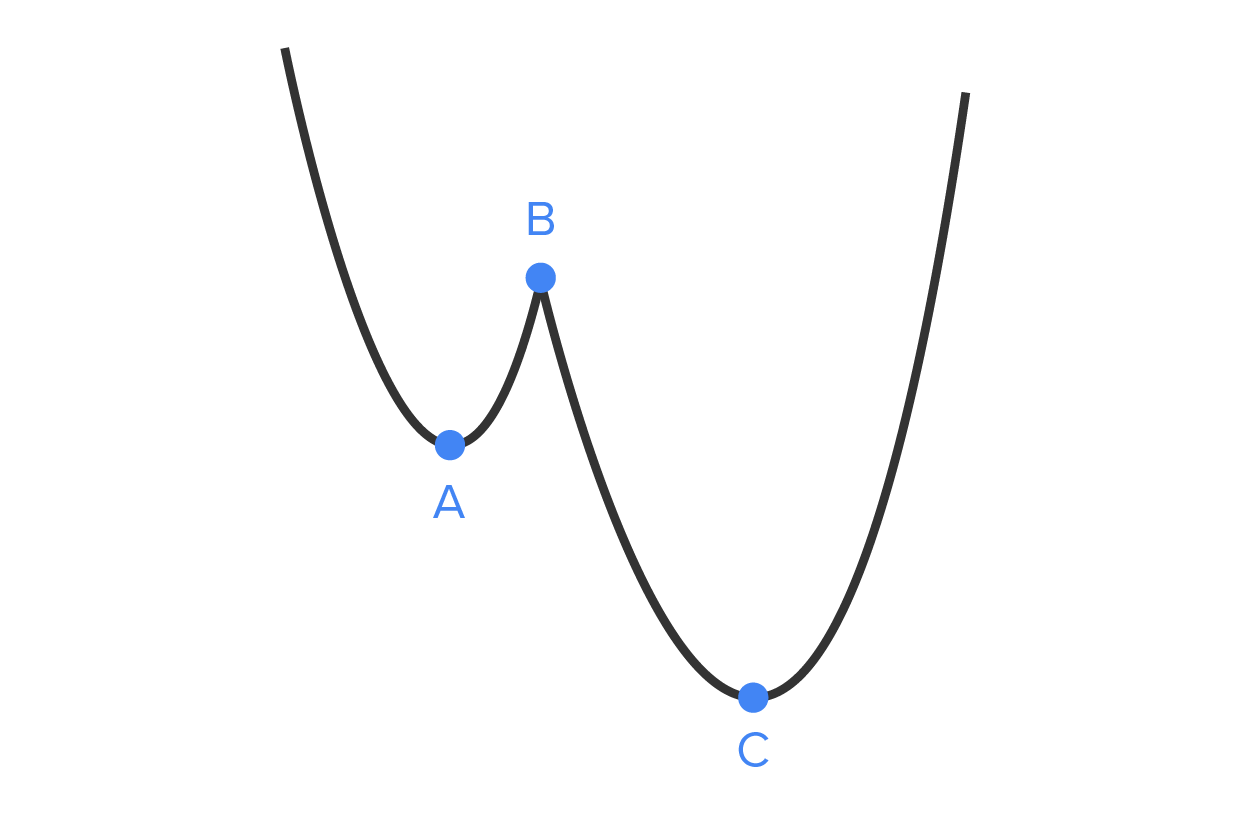
Consider the graph of a function 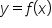y equals f open parentheses x close parentheses, shown here:

A curve falls to a minimum at a marked point labeled ‘A’, then rises to a sharp peak at a marked point labeled ‘B’, falls again sharply to a minimum at a marked point labeled ‘C’, and then extends upward. Point ‘C’ is lower than Point ‘A’.

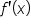  • At point A, f apostrophe open parentheses x close parentheses equals 0.
  • At point B, f apostrophe open parentheses x close parentheses is undefined.
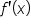  • At point C, f apostrophe open parentheses x close parentheses equals 0.
As discussed in the previous tutorial, values of x in the domain of f open parentheses x close parentheses where f apostrophe open parentheses x close parentheses equals 0 or f apostrophe open parentheses x close parentheses is undefined are called critical numbers.

Therefore, critical numbers can tell us where local maximum or minimum values could occur.

However, the only way to find out is through further analysis, which will be covered in a future challenge.

step by step
To identify relative extrema:
  1. Find all critical values.
  2. Use a graph of the function to determine which critical numbers correspond to which relative extreme points.

Now that we know the connection between critical numbers and extrema, let’s look at a few examples.

2. Finding Local Extrema

EXAMPLE

Consider the function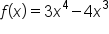 f open parentheses x close parentheses equals 3 x to the power of 4 minus 4 x cubed. First, find all critical numbers:

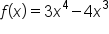
f open parentheses x close parentheses equals 3 x to the power of 4 minus 4 x cubed Start with the original function; the domain is all real numbers.
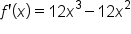
f apostrophe open parentheses x close parentheses equals 12 x cubed minus 12 x squared Take the derivative.
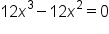
12 x cubed minus 12 x squared equals 0 Since 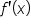f apostrophe open parentheses x close parentheses is a polynomial, it is never undefined. Set f apostrophe open parentheses x close parentheses equals 0 and solve.
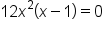
12 x squared open parentheses x minus 1 close parentheses equals 0 Factor.
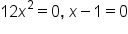
12 x squared equals 0 comma space x minus 1 equals 0 Set each factor equal to 0.
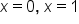
x equals 0 comma space x equals 1 Solve.

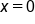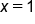Thus, the critical numbers are x equals 0 and x equals 1.

Now, the graph of f open parentheses x close parentheses is shown.

A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10. It has a curve that moves downward from the second quadrant, passes through a marked point at (0, 0), falls slightly, and reaches another marked point at (1, −1) before rising into the first quadrant.

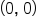The point open parentheses 0 comma space 0 close parentheses is neither a local maximum nor a local minimum, while a local minimum (also a global minimum) occurs at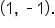 open parentheses 1 comma space short dash 1 close parentheses.

try it
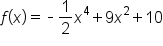Consider the function f open parentheses x close parentheses equals short dash 1 half x to the power of 4 plus 9 x squared plus 10.
Find all critical numbers of f, then determine the local minimum and maximum points by using a graph.
The critical numbers are the values of x for which f apostrophe open parentheses x close parentheses equals 0 or possibly undefined.

First, find f apostrophe open parentheses x close parentheses equals short dash 2 x cubed plus 18 x.

Since this is a polynomial, there is no possibility of f apostrophe open parentheses x close parentheses being undefined.

Setting equal to 0 and solve:

short dash 2 x cubed plus 18 x equals 0
short dash 2 x open parentheses x squared minus 9 close parentheses equals 0
short dash 2 x open parentheses x plus 3 close parentheses open parentheses x minus 3 close parentheses equals 0
short dash 2 x equals 0 comma space space x plus 3 equals 0 comma space space x minus 3 equals 0
x equals 0 comma space short dash 3 comma space 3

Therefore, the critical numbers are x equals 0 comma -3, and 3.

Substituting each value into f open parentheses x close parentheses comma we have the following:

f open parentheses 0 close parentheses equals short dash 1 half open parentheses 0 close parentheses to the power of 4 plus 9 open parentheses 0 close parentheses squared plus 10 equals 10
f open parentheses short dash 3 close parentheses equals short dash 1 half open parentheses short dash 3 close parentheses to the power of 4 plus 9 open parentheses short dash 3 close parentheses squared plus 10 equals 50.5
f open parentheses 3 close parentheses equals short dash 1 half open parentheses 3 close parentheses to the power of 4 plus 9 open parentheses 3 close parentheses squared plus 10 equals 50.5

By examining a graph, you see that the local minimum is located at open parentheses 0 comma space 10 close parentheses and the local maximum points are located at open parentheses short dash 3 comma space 50.5 close parentheses and open parentheses 3 comma space 50.5 close parentheses.

Here is another example that requires us to pay attention to many details.

EXAMPLE

Find all local minimum and maximum values of the function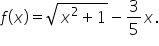 f open parentheses x close parentheses equals square root of x squared plus 1 end root minus 3 over 5 x.

First, we find the critical numbers. Note that the domain of f open parentheses x close parentheses is all real numbers.

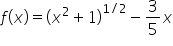
f open parentheses x close parentheses equals open parentheses x squared plus 1 close parentheses to the power of 1 divided by 2 end exponent minus 3 over 5 x Rewrite f open parentheses x close parentheses using exponents to set up differentiation.
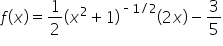
f open parentheses x close parentheses equals 1 half open parentheses x squared plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent open parentheses 2 x close parentheses minus 3 over 5 Find the derivative.
Note that D open square brackets open parentheses x squared plus 1 close parentheses to the power of 1 divided by 2 end exponent close square brackets equals 1 half open parentheses x squared plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent times D open square brackets x squared close square brackets.
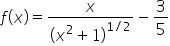
f open parentheses x close parentheses equals x over open parentheses x squared plus 1 close parentheses to the power of 1 divided by 2 end exponent minus 3 over 5 Simplify the first term, then write 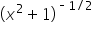open parentheses x squared plus 1 close parentheses to the power of short dash 1 divided by 2 end exponent in terms of positive exponents.
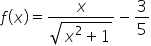
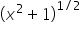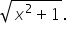
f open parentheses x close parentheses equals fraction numerator x over denominator square root of x squared plus 1 end root end fraction minus 3 over 5 Rewrite open parentheses x squared plus 1 close parentheses to the power of 1 divided by 2 end exponent as square root of x squared plus 1 end root.
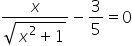
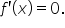
fraction numerator x over denominator square root of x squared plus 1 end root end fraction minus 3 over 5 equals 0 Set f apostrophe open parentheses x close parentheses equals 0.
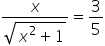
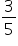fraction numerator x over denominator square root of x squared plus 1 end root end fraction equals 3 over 5 Add 3 over 5 to both sides.
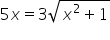
5 x equals 3 square root of x squared plus 1 end root Cross multiply.
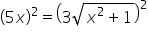
open parentheses 5 x close parentheses squared equals open parentheses 3 square root of x squared plus 1 end root close parentheses squared Since a variable is under a square root, square both sides.
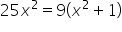
25 x squared equals 9 open parentheses x squared plus 1 close parentheses Simplify.
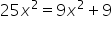
25 x squared equals 9 x squared plus 9 Distribute on the right-hand side.
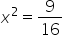
x squared equals 9 over 16 Subtract 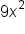9 x squared from both sides, then divide both sides by 16.
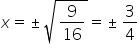
x equals plus-or-minus square root of 9 over 16 end root equals plus-or-minus 3 over 4 Apply the square root principle. Remember that this yields both a positive and a negative solution!

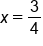You may recall that when solving equations by squaring both sides, it’s possible to get extraneous solutions. While x equals 3 over 4 solves the original equation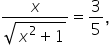 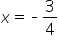fraction numerator x over denominator square root of x squared plus 1 end root end fraction equals 3 over 5 comma x equals short dash 3 over 4 does not. To see this, substitute 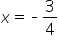x equals short dash 3 over 4 into the equation – you will get 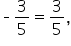short dash 3 over 5 equals 3 over 5 comma which is not true.

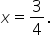
Therefore, the only critical number is x equals 3 over 4.

The graph of f open parentheses x close parentheses is shown below.

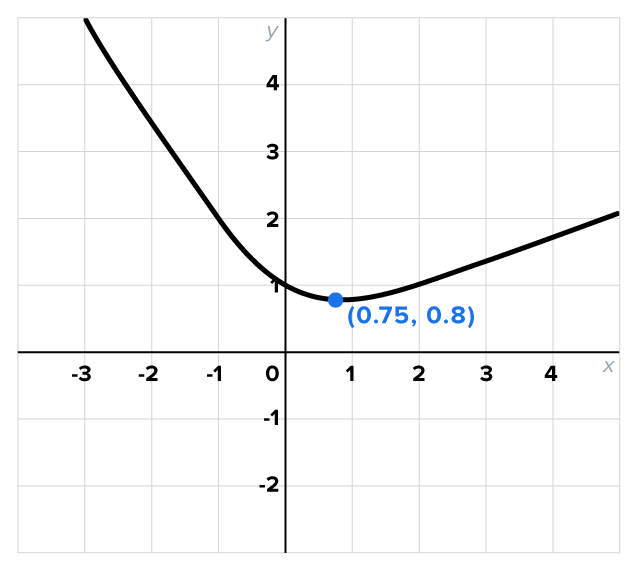
A graph with an x-axis ranging from −3 to 4 and a y-axis ranging from −2 to 4. A curve descends from the second quadrant, passes through the point (0, 1) and the marked point at (0.75, 0.8), and extends upward to the right, beyond the point (4, 1.7) in the first quadrant.

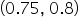As you can see, the point open parentheses 0.75 comma space 0.8 close parentheses is a low point on the graph, therefore there is a local minimum value of 0.8 when x equals 0.75.

summary
In this lesson, you learned about the relationship between critical numbers and local extrema, which is that critical numbers help locate the coordinates of local maximum and minimum points. Understanding this connection between critical numbers and extrema, you practiced finding local extrema of a function by first determining all critical numbers. 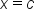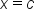As you saw with one example, a critical number at x equals c doesn’t automatically imply that there is a local maximum or minimum at x equals c.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.