Table of Contents |
If a function  is continuous on a closed interval
is continuous on a closed interval 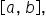 then
then  is guaranteed to have global maximum and global minimum values on the interval
is guaranteed to have global maximum and global minimum values on the interval 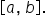 This is known as the extreme value theorem.
This is known as the extreme value theorem.
Here is an illustration of the extreme value theorem:
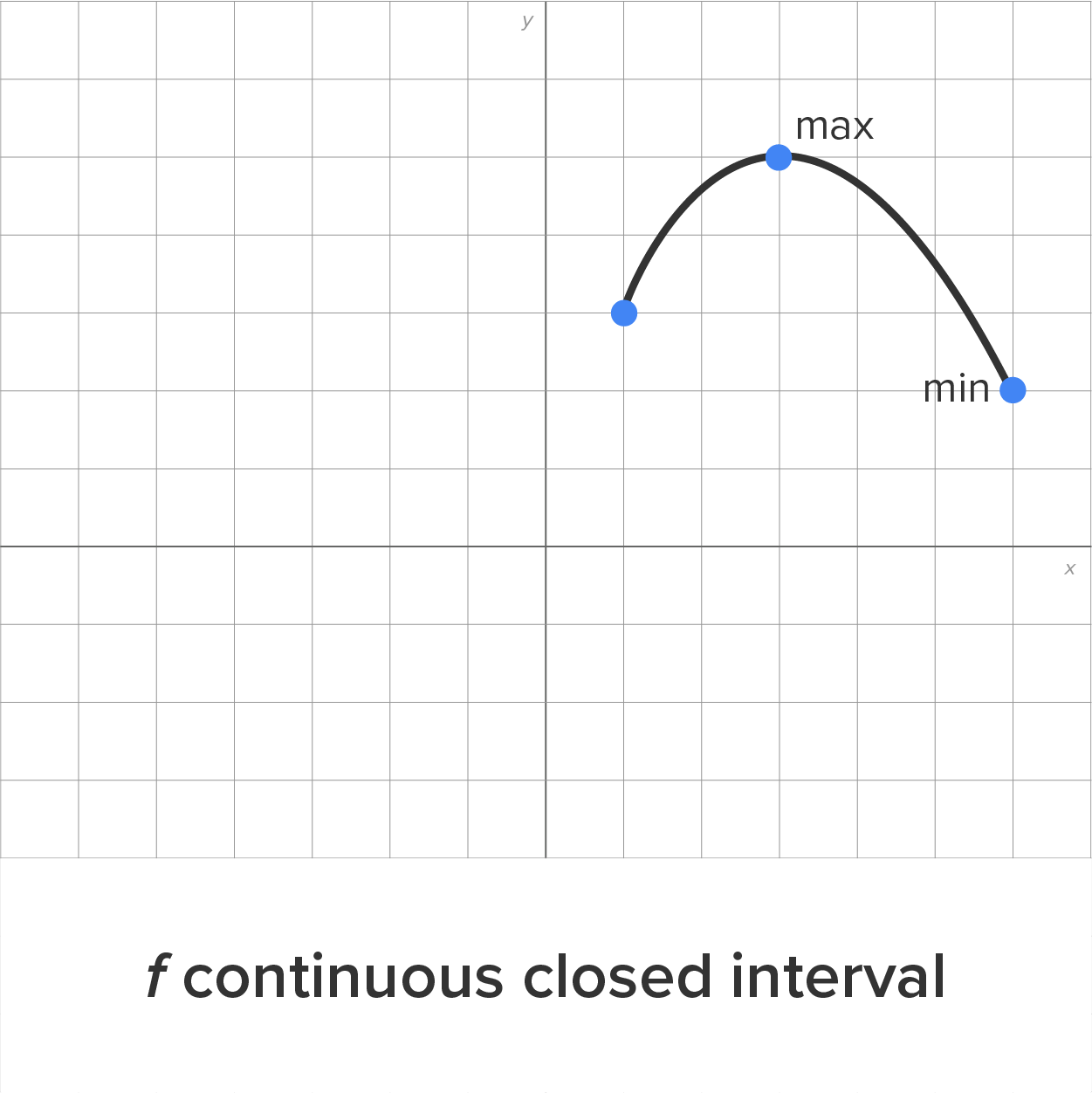
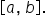
| f Continuous Open Interval | f Continuous Open Interval | f Not Continuous Closed Interval |
|---|---|---|

|
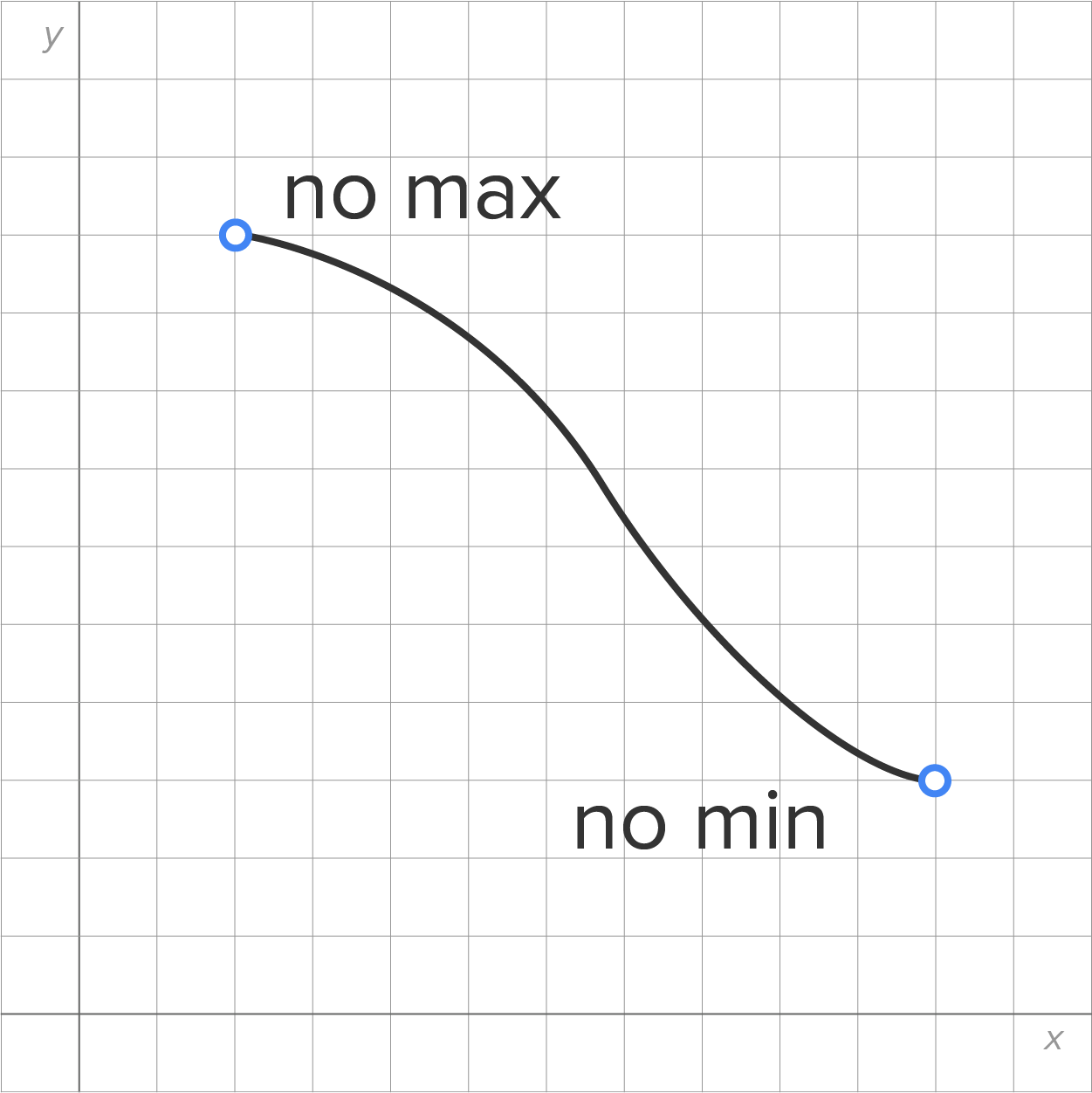
|
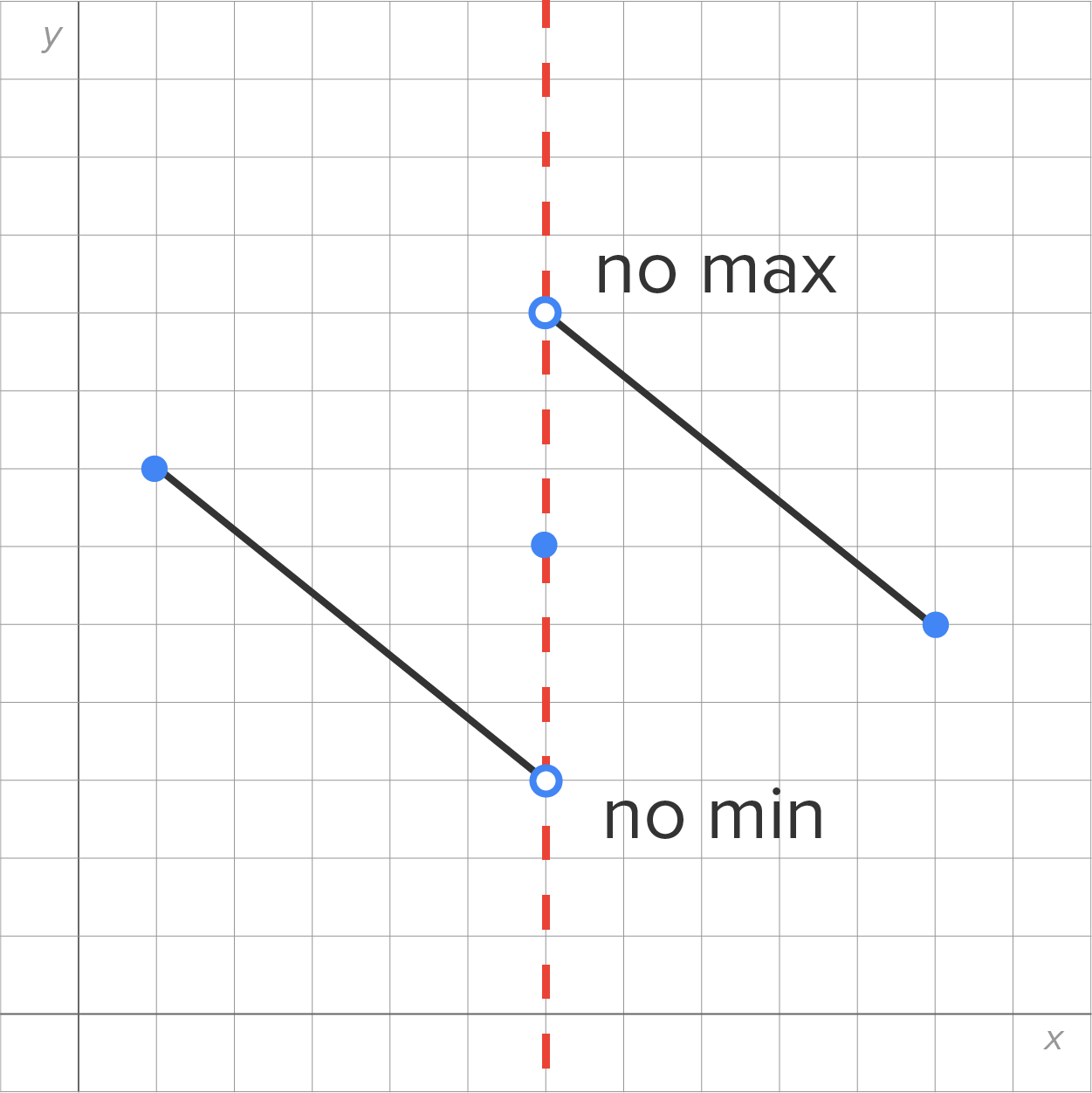
|
 is a continuous function on some closed interval
is a continuous function on some closed interval 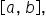 then
then  has global maximum and global minimum values on the interval
has global maximum and global minimum values on the interval 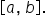
As a result of the theorem, here is what we need to do in order to find the global minimum and maximum values of  on a closed interval
on a closed interval 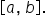
 that are in the interval
that are in the interval 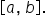
 at each endpoint and each critical number. The largest value of f is the global maximum and the smallest value of f is the global minimum.
at each endpoint and each critical number. The largest value of f is the global maximum and the smallest value of f is the global minimum. EXAMPLE
Find the global maximum and minimum points of the function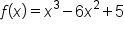 on the interval
on the interval 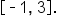
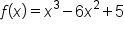
|
Start with the original function. |
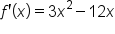
|
Take the derivative. |
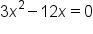 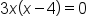 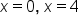
|
Since 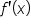 is a polynomial, it is never undefined. Set is a polynomial, it is never undefined. Set  and solve for x. and solve for x.
|
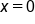 and
and 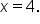
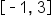 is considered, the critical value
is considered, the critical value  is not used.
is not used.
 at the endpoints,
at the endpoints, 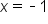 and
and 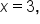 and the remaining critical number,
and the remaining critical number, 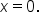
| x |
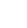
|
Result |
|---|---|---|
| -1 |
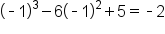
|
Neither a Global Maximum or Global Minimum |
| 0 |
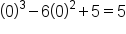
|
Global Maximum |
| 3 |
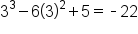
|
Global Minimum |
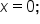 and the global minimum value is -22 and occurs when
and the global minimum value is -22 and occurs when 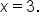
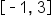 is shown below, which confirms the results.
is shown below, which confirms the results.

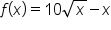 on the interval
on the interval 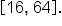
When finding critical numbers, it’s important to consider only those that are in the interval 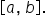 Here is an example that helps illustrate this.
Here is an example that helps illustrate this.
EXAMPLE
Find all global extreme values of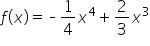 on the interval
on the interval 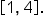
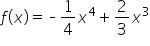
|
Start with the original function. |
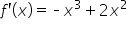
|
Use the power rule to find the derivative. |
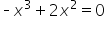
|
Set 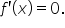
|
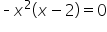
|
Factor out 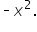
|
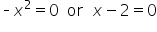
|
Set each factor equal to 0. |
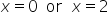
|
Solve each equation. |
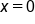 and
and 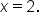
 notice that
notice that 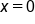 is not contained in this interval. This means that
is not contained in this interval. This means that 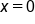 is not considered in any further analysis.
is not considered in any further analysis.
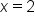 along with the endpoints of the interval,
along with the endpoints of the interval, 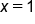 and
and 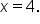
 Note the approximations are also provided to make comparisons easier.
Note the approximations are also provided to make comparisons easier.
| x | 1 | 2 | 4 |
|---|---|---|---|
| f (x ) |
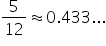
|
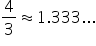
|
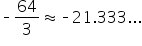
|
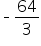 when
when 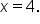 and the global maximum value is
and the global maximum value is 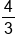 when
when 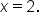
 is continuous on a closed interval, the extreme value theorem guarantees a global minimum value and a global maximum value at some location within the closed interval. Then, you applied this theorem to find extreme values of a continuous function on a closed interval, by first finding all critical numbers of
is continuous on a closed interval, the extreme value theorem guarantees a global minimum value and a global maximum value at some location within the closed interval. Then, you applied this theorem to find extreme values of a continuous function on a closed interval, by first finding all critical numbers of  that are in the interval
that are in the interval 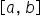 , then evaluating
, then evaluating  at each endpoint and each critical number. This concept is going to be very useful once we use derivatives to solve optimization problems.
at each endpoint and each critical number. This concept is going to be very useful once we use derivatives to solve optimization problems.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.