Table of Contents |
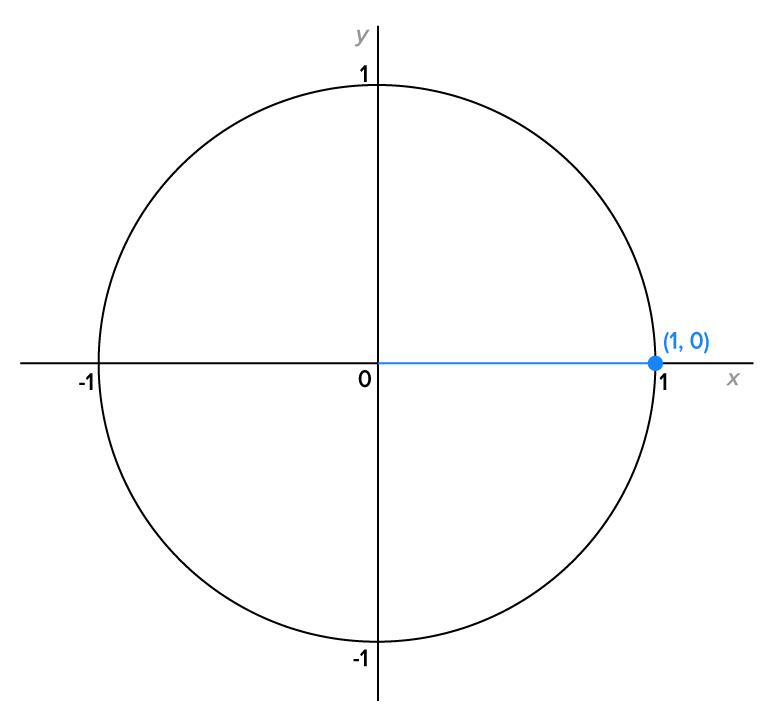
The unit circle is a circle of radius 1 that is centered at the origin. Consider the graph below.
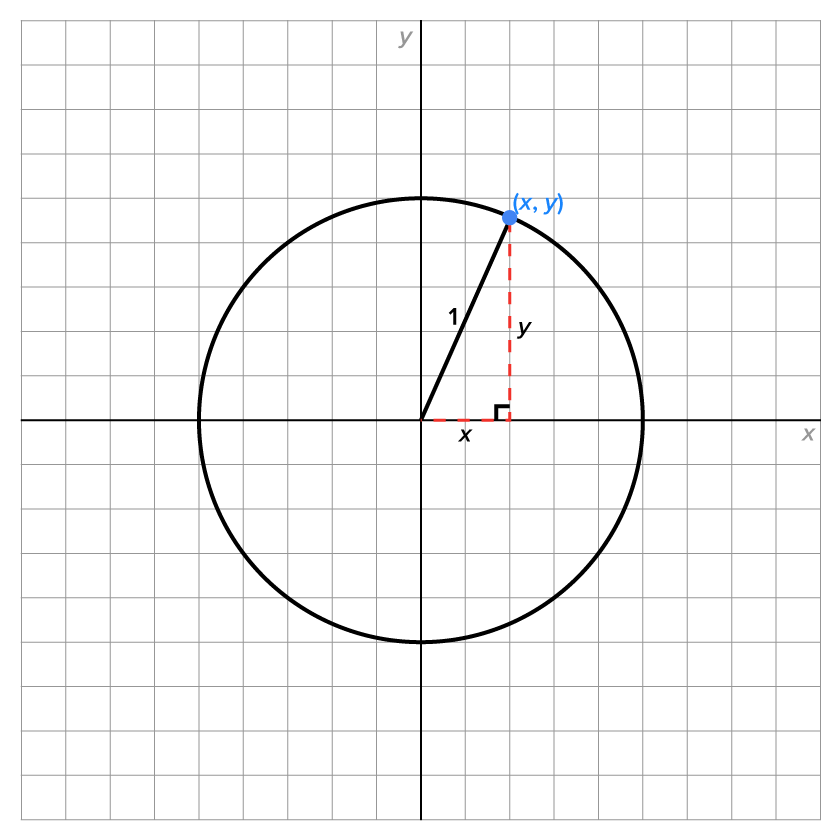
Using the Pythagorean theorem, 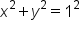 , or more simply,
, or more simply, 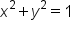 . This is true for any point on the unit circle. The equation of the unit circle is
. This is true for any point on the unit circle. The equation of the unit circle is 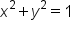 .
.
Next, consider the figure below, which shows the unit circle and other information:
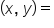 a point on the circle.
a point on the circle.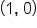 to
to 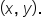
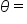 the central angle of the circular arc.
the central angle of the circular arc.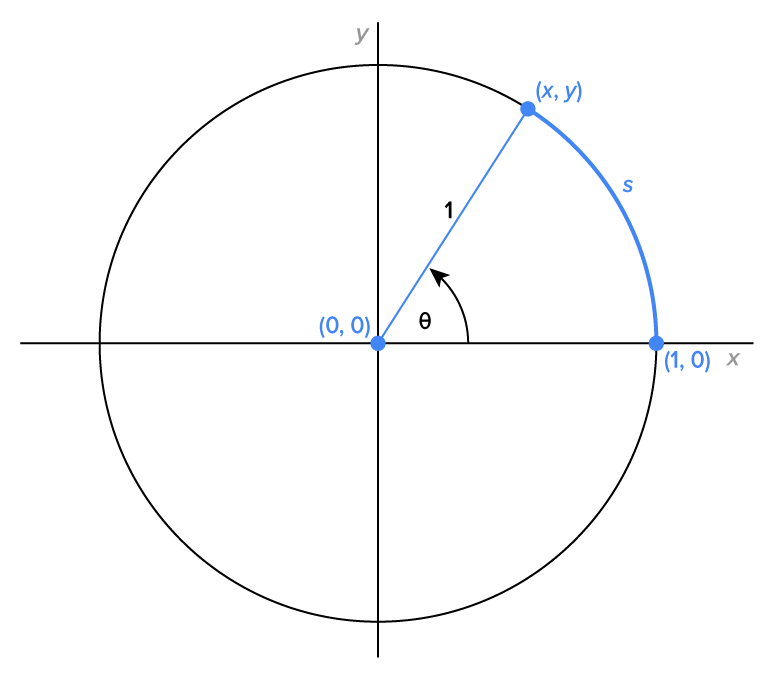
Every point 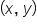 corresponds to the length s of some circular arc. This means that x and y can be defined as functions of s, meaning s is the input, and x and y are outputs.
corresponds to the length s of some circular arc. This means that x and y can be defined as functions of s, meaning s is the input, and x and y are outputs.
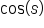 and represents the x-coordinate of the point. That is,
and represents the x-coordinate of the point. That is, 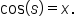
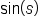 and represents the y-coordinate of the point. That is,
and represents the y-coordinate of the point. That is, 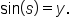
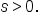 If
If 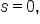 then there is no length, which means no movement from the point
then there is no length, which means no movement from the point 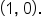 Thus, every real number s is paired with one point on the graph of the unit circle. This means that the domain of the sine and cosine functions is the set of all real numbers, or
Thus, every real number s is paired with one point on the graph of the unit circle. This means that the domain of the sine and cosine functions is the set of all real numbers, or 
Now, how does the length s relate to the angle 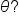
Since 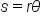 and
and 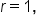 we have
we have 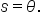
Thus, we can also express the sine and cosine function in terms of the angle, as well as its length.
To summarize, any point on the unit circle can be expressed as 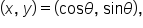 where
where  is the central angle of the arc; or
is the central angle of the arc; or 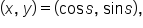 where s is the length of the arc. As you progress through this course, you will notice that using the angle as input becomes necessary to make more general definitions.
where s is the length of the arc. As you progress through this course, you will notice that using the angle as input becomes necessary to make more general definitions.
 or
or 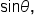 respectively.
respectively.
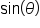 and
and 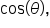 but just like the logarithmic functions, we usually only use grouping symbols when there is more than a single variable as the input.
but just like the logarithmic functions, we usually only use grouping symbols when there is more than a single variable as the input.
 is the input, you will write
is the input, you will write 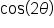 as opposed to
as opposed to 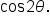 Some textbooks use the latter, and this is mathematically correct, but it is always best to emphasize the input by placing grouping symbols around it.
Some textbooks use the latter, and this is mathematically correct, but it is always best to emphasize the input by placing grouping symbols around it.
EXAMPLE
Consider the point P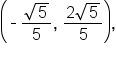 which is a point on the unit circle since it satisfies the equation
which is a point on the unit circle since it satisfies the equation 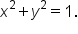
 be the angle of inclination from the positive x-axis to the line connecting the origin to P, as shown in the figure.
be the angle of inclination from the positive x-axis to the line connecting the origin to P, as shown in the figure.

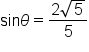 and
and 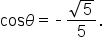
Let’s say that angle  terminates at some ray that intersects the unit circle at some point
terminates at some ray that intersects the unit circle at some point  Then, any angle coterminal to
Then, any angle coterminal to  will also terminate at the same ray, which means the values of sine and cosine are the same as they were at the angle
will also terminate at the same ray, which means the values of sine and cosine are the same as they were at the angle  This results in the following property.
This results in the following property.
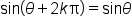 and
and 
Since a sine or cosine function can be applied to any angle, the domain of both functions is the set of all real numbers.
Considering all possible points on the unit circle, we see that 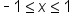 and
and 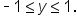
Since 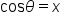 and
and  for any point
for any point 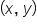 on the unit circle, this means that
on the unit circle, this means that 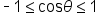 and
and 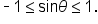
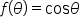 and
and 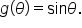 Each function has domain
Each function has domain 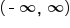 and range
and range 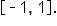
When substituting certain values of  into the sine and cosine functions, we can refer to the unit circle to find these values. These special angles are:
into the sine and cosine functions, we can refer to the unit circle to find these values. These special angles are:
| Degrees |
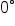
|
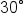
|
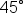
|
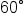
|
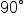
|
|---|---|---|---|---|---|
| Radians | 0 |
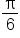
|
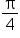
|
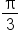
|
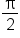
|
Let’s say we want the value of the sine function when the angle is 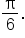 You would write
You would write 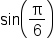 when the angle is in radian form, which is equivalent to
when the angle is in radian form, which is equivalent to 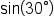 when the angle is in degree form.
when the angle is in degree form.
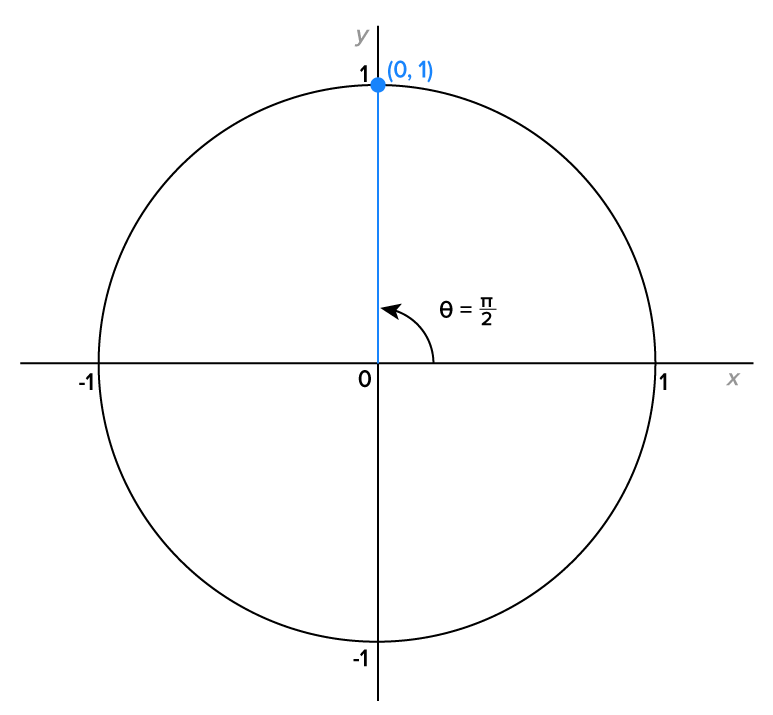
To start, let’s consider 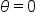 radians, which is also
radians, which is also 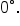
Since 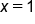 and
and 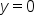 when
when 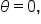 it follows that
it follows that 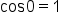 and
and 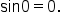
Along the same line of thinking, let’s now consider  or in degrees,
or in degrees, 
Since 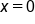 and
and 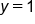 when
when  it follows that
it follows that 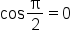 and
and 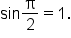
Now, let’s find the values at 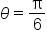 and
and 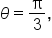 which are
which are 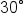 and
and 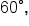 respectively.
respectively.
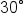 and
and 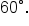
Now, consider the angle 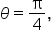 or in degrees,
or in degrees, 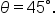 Since it is easier to visualize, we’ll use degree measures to illustrate.
Since it is easier to visualize, we’ll use degree measures to illustrate.
Consider this figure.
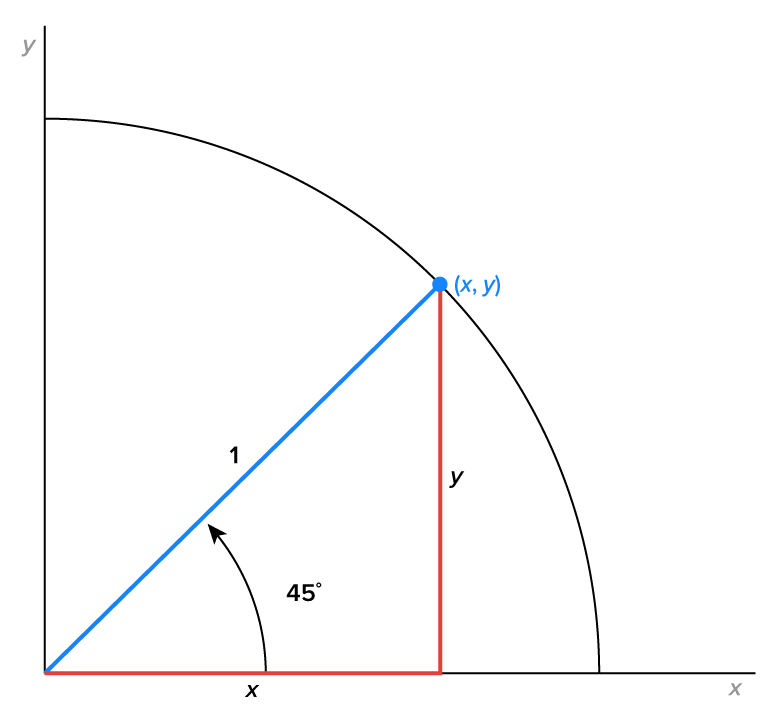
We know the following:
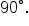
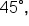 since the sum of the angles in a triangle is
since the sum of the angles in a triangle is 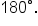
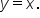
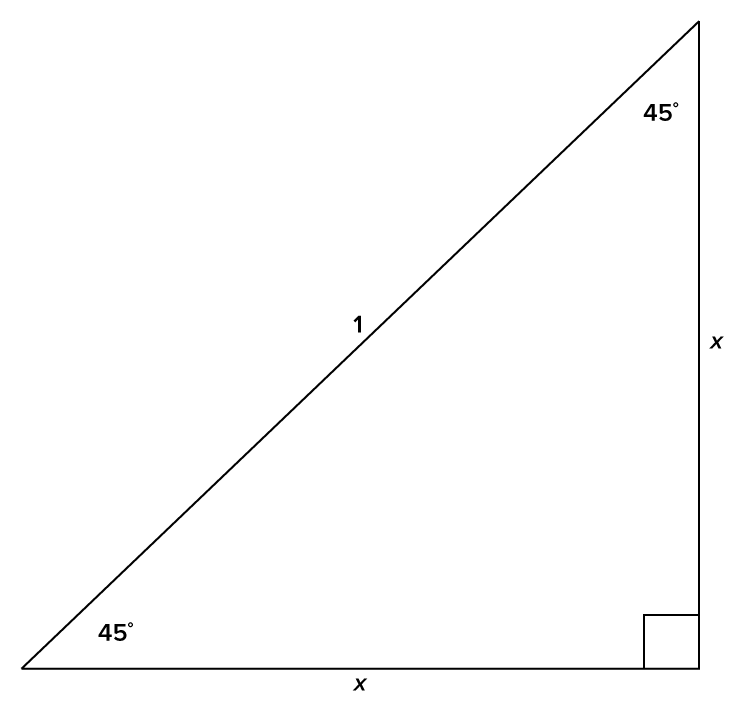
By using the Pythagorean theorem, we can find the value of x.
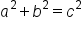
|
This is the Pythagorean theorem. |
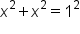
|
Substitute the quantities. Since 1 is the hypotenuse, 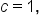 then other sides are each x. then other sides are each x.
|
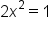
|
Combine like terms. |
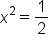
|
Divide both sides by 2. |
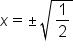
|
Apply the square root principle. |

|
Since the point is in the first quadrant, use the positive solution. |
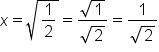
|
Rewrite as a quotient of square roots and simplify the numerator. |
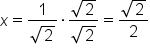
|
Rationalize the denominator. |
This means that 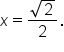 Since
Since 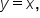 it follows that
it follows that 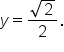 Thus, the terminal point on the arc of the circle is
Thus, the terminal point on the arc of the circle is 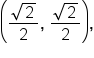 which means
which means 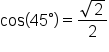 and
and  In radian form,
In radian form, 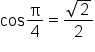 and
and 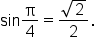
To summarize, we have the following table, which organizes the values of the sine and cosine functions for each special angle.
 in Degrees in Degrees
|
|
|
|
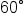
|
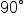
|
|---|---|---|---|---|---|
 in Radians in Radians
|
0 |
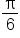
|
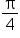
|
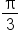
|
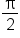
|

|
1 |
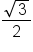
|
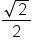
|
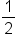
|
0 |

|
0 |
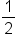
|
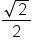
|
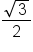
|
1 |
Consider this picture below, which shows the signs of the coordinates in each quadrant:

Since 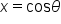 and
and 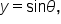 we can make the following observations:
we can make the following observations:
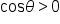 in quadrants I and IV and
in quadrants I and IV and 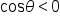 in quadrants II and III.
in quadrants II and III. 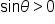 in quadrants I and II and
in quadrants I and II and 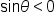 in quadrants III and IV.
in quadrants III and IV.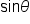 and
and  are positive in quadrant I and are both negative in quadrant III.
are positive in quadrant I and are both negative in quadrant III.
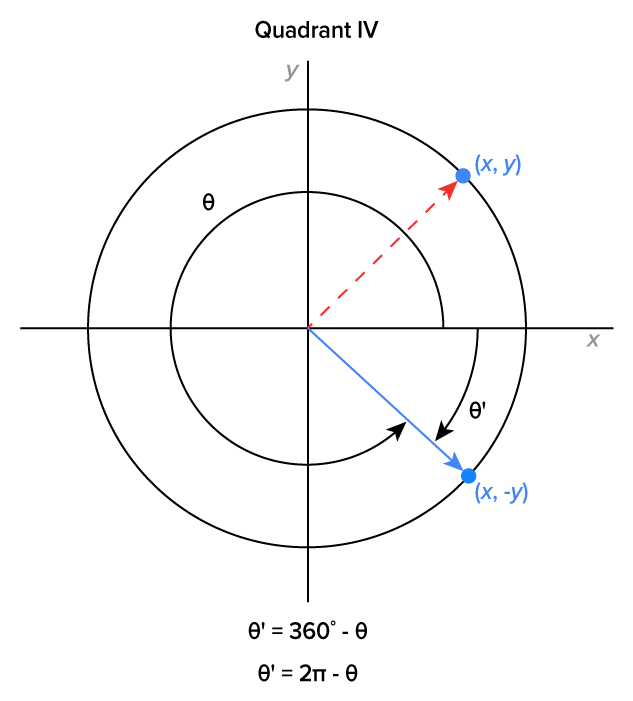
To evaluate trigonometric functions for angles that terminate outside the first quadrant, we need to use reference angles.
For the purposes of this exploration, let’s assume that angle  terminates in quadrant I, and corresponds to the point
terminates in quadrant I, and corresponds to the point 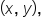 where x and y are positive. Our goal is to determine a relationship between
where x and y are positive. Our goal is to determine a relationship between  and the angles that correspond to the points
and the angles that correspond to the points 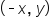 in quadrant II,
in quadrant II, 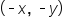 in quadrant III, and
in quadrant III, and 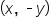 in quadrant IV.
in quadrant IV.
First, let’s examine a quadrant II angle.
Let 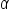 be an angle that terminates in quadrant II, and corresponds to the point
be an angle that terminates in quadrant II, and corresponds to the point  as shown in the figure.
as shown in the figure.
The cosines of the angles are opposites of each other since the x-coordinates are opposites. The sines of the angles are equal since the y-coordinates are equal.
Now notice the angle  which has the same measure as
which has the same measure as  and is the smallest positive angle between
and is the smallest positive angle between  and the x-axis. If the coordinates are known in the first quadrant, then using
and the x-axis. If the coordinates are known in the first quadrant, then using 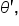 which is the reference angle, tells us the values of the coordinates in the second quadrant, since they have the same magnitude, but possibly different sign.
which is the reference angle, tells us the values of the coordinates in the second quadrant, since they have the same magnitude, but possibly different sign.
Seeing this now, here is a picture that shows what’s happening for angles that terminate in each quadrant. The formulas below each graph are used to calculate the reference angle in both degree form and in radian form.
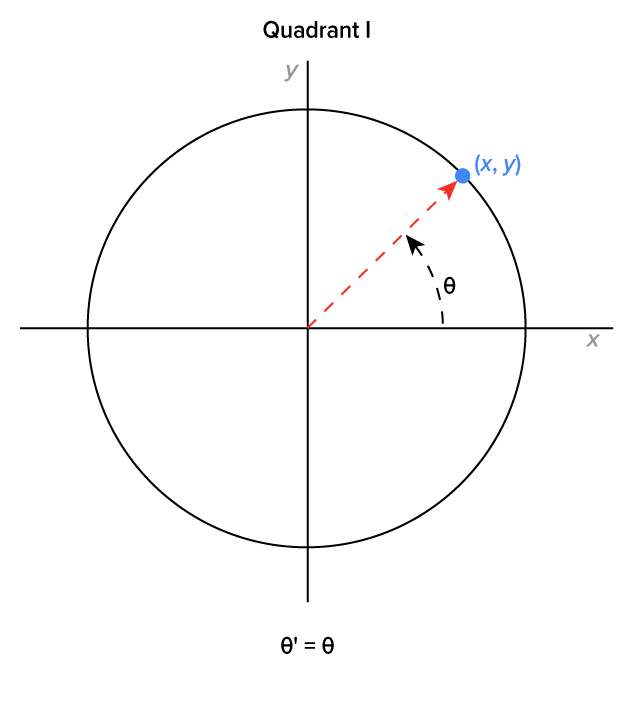
|
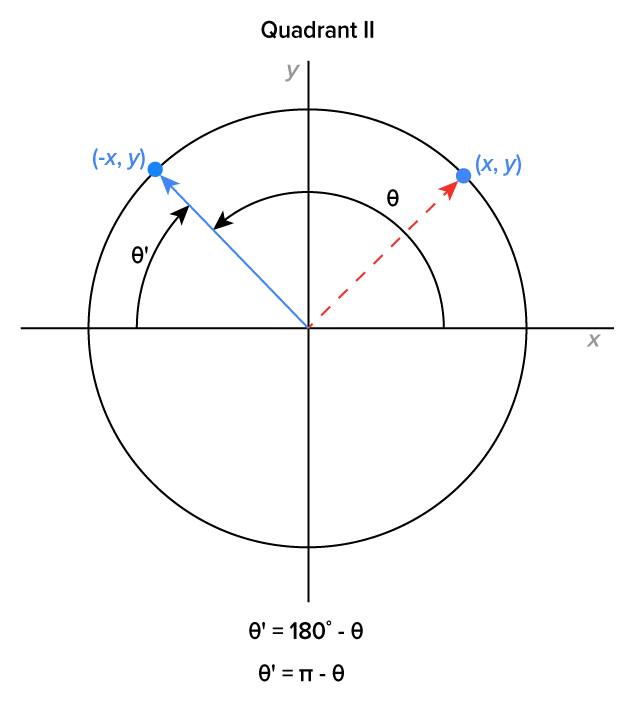
|
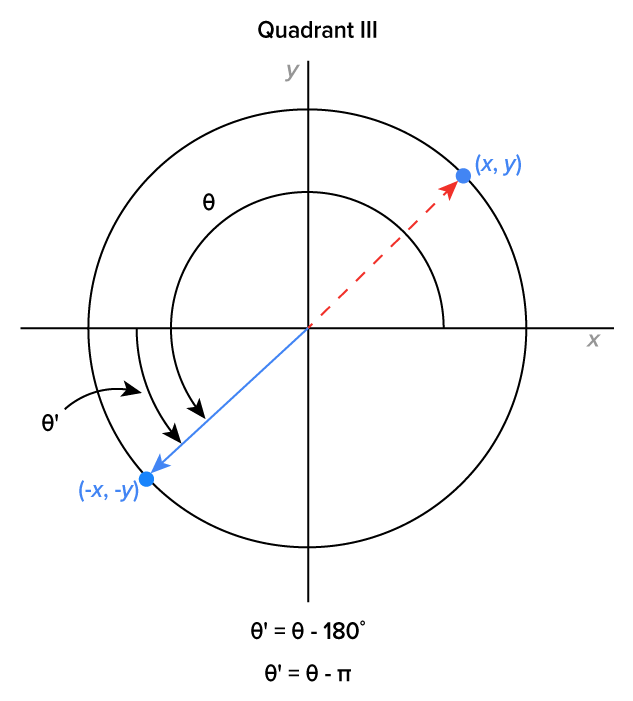
|
|
In each case,  is the reference angle. Note that the measure of
is the reference angle. Note that the measure of  is the same as the angle between the positive x-axis and the ray in the first quadrant each time.
is the same as the angle between the positive x-axis and the ray in the first quadrant each time.
EXAMPLE
Find the exact value of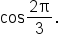
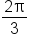 is
is 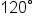 in degree form. The angle is sketched below.
in degree form. The angle is sketched below.

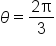 terminates in quadrant II, the reference angle is
terminates in quadrant II, the reference angle is 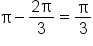 , or
, or 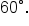
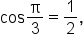 it follows that
it follows that  since x-coordinates are negative in quadrant II.
since x-coordinates are negative in quadrant II.
EXAMPLE
Find the exact value of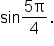
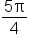 is
is 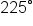 in degree form. The angle is sketched below.
in degree form. The angle is sketched below.
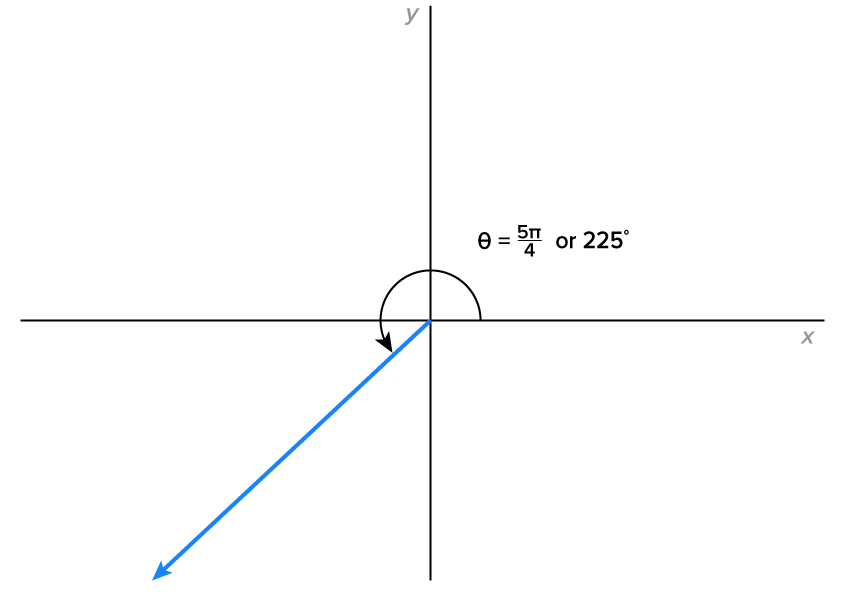
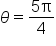 terminates in quadrant III, the reference angle is
terminates in quadrant III, the reference angle is 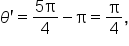 or
or 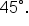
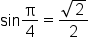 and y-coordinates are negative in quadrant III,
and y-coordinates are negative in quadrant III, 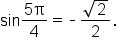
Here is one more example, this time using an angle that terminates in quadrant IV.
EXAMPLE
Evaluate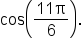
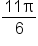 is equivalent to
is equivalent to 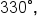 which means that it terminates in quadrant IV. A sketch of the angle is shown below.
which means that it terminates in quadrant IV. A sketch of the angle is shown below.
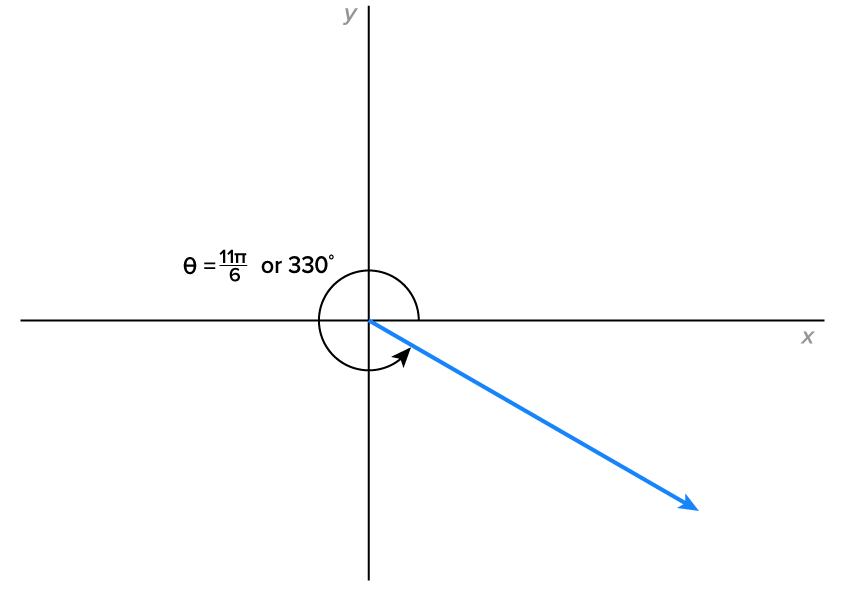
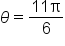 terminates in quadrant IV, the reference angle is
terminates in quadrant IV, the reference angle is 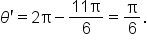
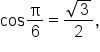 it follows that
it follows that 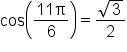 since x-coordinates are positive in quadrant IV.
since x-coordinates are positive in quadrant IV.
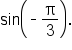
Using the unit circle, we can define four more trigonometric functions, all based on the angle  and point
and point 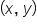 on the unit circle:
on the unit circle:
 is written
is written 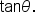 It is the ratio of the y-coordinate to the x-coordinate. That is,
It is the ratio of the y-coordinate to the x-coordinate. That is,  where
where 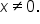
 is written
is written 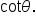 It is the ratio of the x-coordinate to the y-coordinate. That is,
It is the ratio of the x-coordinate to the y-coordinate. That is, 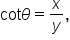 where
where  Notice that this is the reciprocal of the tangent function.
Notice that this is the reciprocal of the tangent function.  is written
is written 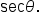 It is the reciprocal of the x-coordinate. That is,
It is the reciprocal of the x-coordinate. That is, 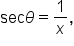 where
where 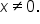 Notice that this is the reciprocal of the cosine function.
Notice that this is the reciprocal of the cosine function.  is written
is written 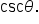 It is the reciprocal of the y-coordinate. That is,
It is the reciprocal of the y-coordinate. That is, 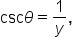 where
where  Notice that this is the reciprocal of the sine function.
Notice that this is the reciprocal of the sine function. 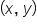 on the unit circle, and angle
on the unit circle, and angle  that inclines from the positive x-axis to the line with endpoints
that inclines from the positive x-axis to the line with endpoints 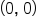 and
and 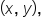 we have the following definitions of the remaining four trigonometric functions:
we have the following definitions of the remaining four trigonometric functions:
 where
where 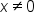
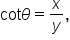 where
where 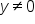
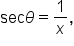 where
where 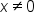
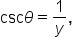 where
where 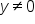
With these definitions, let’s revert back to the unit circle to understand the domain of these functions. We’ll explore the range of these functions when we examine their graphs later in this course.
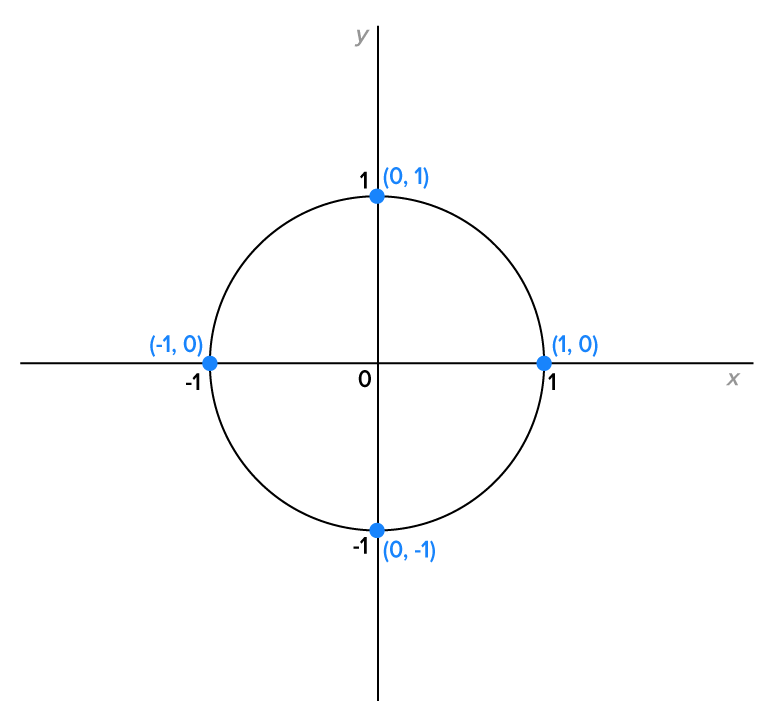
To examine the domains of these trigonometric functions, the information is organized in the chart.
| Trigonometric Function and Its Ratio From the Unit Circle | Undefined at These Points on the Unit Circle |
Undefined for These Values of 
|
Domain of Function |
|---|---|---|---|
 where where 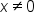
|
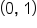 and and 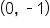
|
 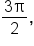 plus all coterminal angles plus all coterminal angles
|
All real numbers except for odd multiples of 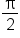
|
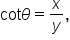 where where 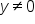
|
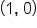 and and 
|
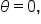 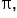 plus all coterminal angles plus all coterminal angles
|
All real numbers except all integer multiples of 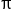
|
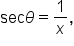 where where 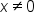
|
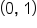 and and 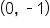
|
 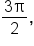 plus all coterminal angles plus all coterminal angles
|
All real numbers except for odd multiples of 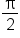
|
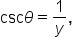 where where 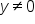
|
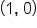 and and 
|
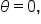 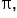 plus all coterminal angles plus all coterminal angles
|
All real numbers except all integer multiples of 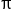
|
Taking all the formulas for these trigonometric functions and replacing x with  and y with
and y with 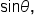 we have the following identities.
we have the following identities.
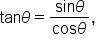 where
where 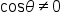
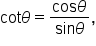 where
where 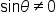
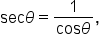 where
where 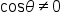
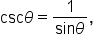 where
where 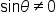
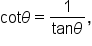 where
where 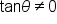 and
and 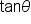 is defined
is definedThere are six trigonometric functions total, but three of them are reciprocals of the other three. In practice, it is easier to find the values of sine, cosine, and tangent functions, then take their reciprocals to get the values of the cosecant, secant, and cotangent functions (as long as values are not undefined).
With all these definitions, we can find the values of all six trigonometric functions of an angle 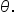
EXAMPLE
Consider the point P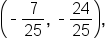 which is a point on the unit circle since it satisfies the equation
which is a point on the unit circle since it satisfies the equation 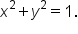
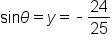
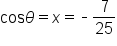
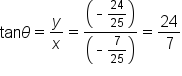
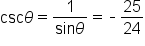
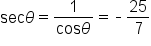
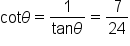
 where the terminal side of
where the terminal side of  intersects the unit circle at the point
intersects the unit circle at the point 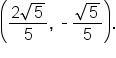
Using the values of  and
and 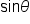 at special angles, we can also find values of the other trigonometric functions.
at special angles, we can also find values of the other trigonometric functions.
EXAMPLE
Find the exact values of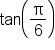 and
and 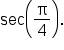
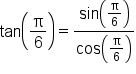
|
Use the identity 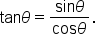
|
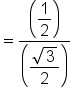
|
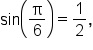 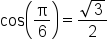
|
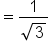
|
Simplify; multiply the numerator and denominator by 2. |
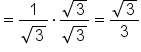
|
Rationalize the denominator. |
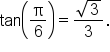
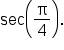
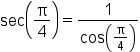
|
Use the identity 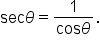
|
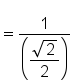
|
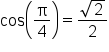
|
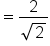
|
Simplify. |
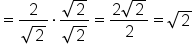
|
Rationalize the denominator and simplify. |
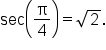
Using the relationships between the trigonometric functions and the coordinates  on the unit circle, we can tell what the sign of the function value is simply by knowing the quadrant in which the angle terminates.
on the unit circle, we can tell what the sign of the function value is simply by knowing the quadrant in which the angle terminates.
For example, consider the fact that 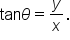 If x and y have the same sign, then
If x and y have the same sign, then 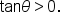 If x and y have different signs, then
If x and y have different signs, then 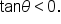 If we repeat this process for all six trigonometric functions and their defined ratios, we could summarize the results this way, listing where the functions return positive values.
If we repeat this process for all six trigonometric functions and their defined ratios, we could summarize the results this way, listing where the functions return positive values.
|
Quadrant II (-, +) |
Quadrant I (+, +) |
|---|---|
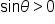 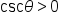
|
All functions are positive. |
|
Quadrant III (-, -) |
Quadrant IV (+, -) |
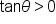 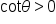
|
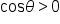 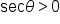
|
If you want a mnemonic to remember this by, just remember All Students Take Calculus!
EXAMPLE
Find the exact value of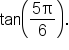
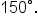 This means that the angle terminates in quadrant II, and has reference angle
This means that the angle terminates in quadrant II, and has reference angle 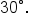 This means that the value of
This means that the value of 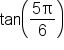 is negative.
is negative.
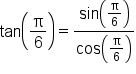
|
Use the identity 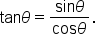
|
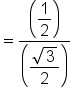
|
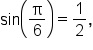 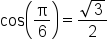
|
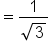
|
Simplify; multiply the numerator and denominator by 2. |
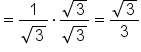
|
Rationalize the denominator. |
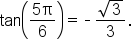
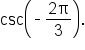
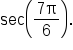
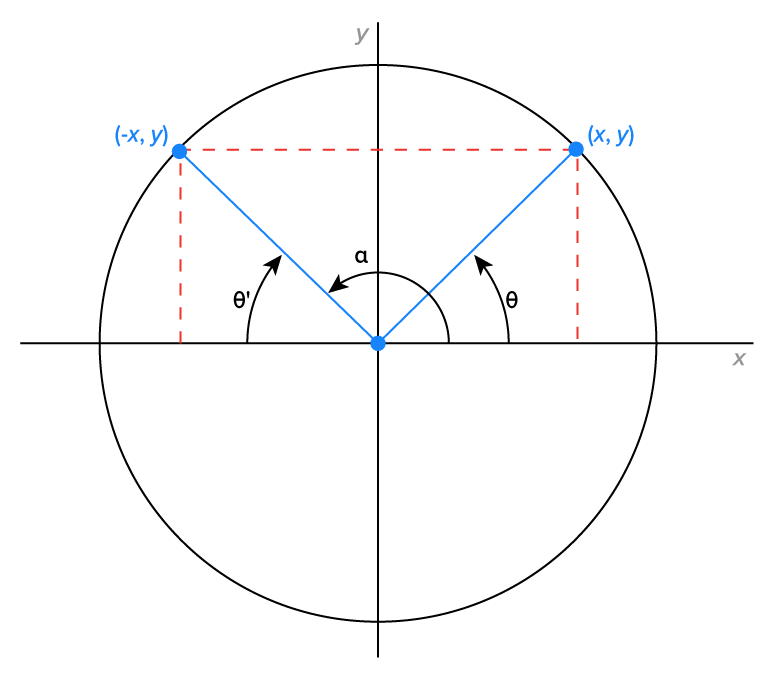
Consider the figure shown below, which shows that angle  corresponds to the point
corresponds to the point 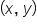 , while the angle
, while the angle 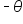 corresponds to the point
corresponds to the point 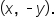
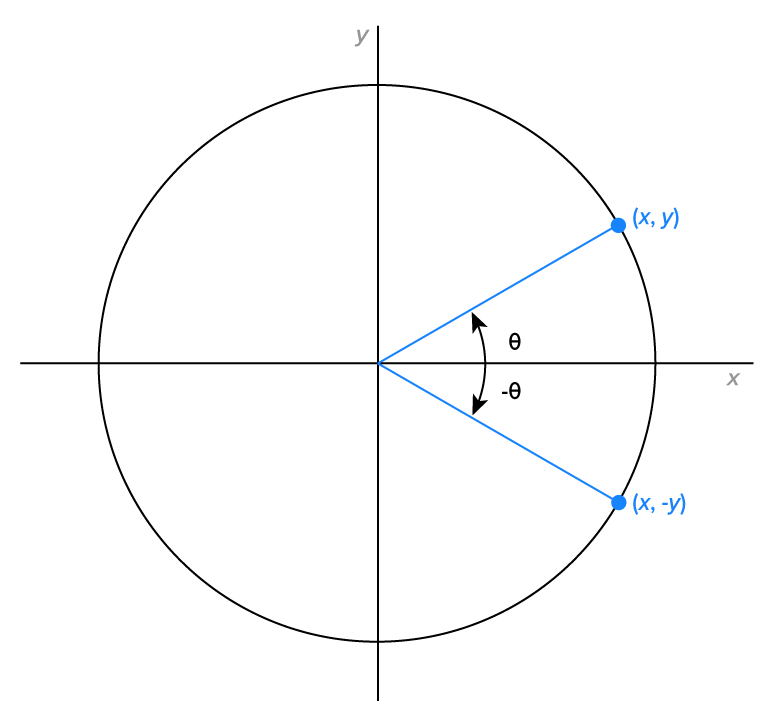
Let’s compare 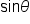 and
and 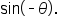 Since the value of the sine function is the y-coordinate of the point, we have
Since the value of the sine function is the y-coordinate of the point, we have  and
and  In general, we can say that
In general, we can say that 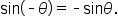
Is this true for all the trigonometric functions?
Let’s compare  and
and 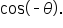 Since the value of the cosine function is the x-coordinate of the point, we have
Since the value of the cosine function is the x-coordinate of the point, we have 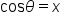 and
and 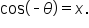 In general, we can say that
In general, we can say that 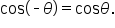
Extending this to the other trigonometric functions, we can establish identities known as the even/odd identities.

Given a function 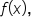 recall that
recall that  is even if
is even if 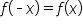 and odd if
and odd if 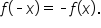
Therefore, the sine, cosecant, tangent, and cotangent functions are odd, while the cosine and secant functions are even.
These identities are useful to evaluate trigonometric functions of negative angles when the function value at the positive angle is known.
EXAMPLE
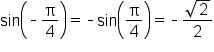
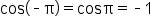
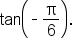
The even/odd identities are very useful when graphing trigonometric functions, which is covered in a future lesson.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.