Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Evaluating Radicals

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to evaluate a given radical. Specifically, this lesson will cover:

Table of Contents

before you start
A new homeowner must clean her gutters, and for that, she needs a ladder. The roofline is 12 feet high. Remembering a classic rule of safety, the homeowner knows a ladder should be placed one fourth of the height away from the side—that is, 3 feet. She goes to the hardware store and finds ladders in sizes from 10 feet to 20 feet.

Which one should she buy?



Solving problems like this are probably the most common use of radicals, or roots. Being able to calculate roots is needed in fields like engineering, architecture, and even (appropriately!) in gardening! As you can see, it can even come up for simple household projects. In this challenge, we will review the ways radicals are evaluated so we can use them in algebra.

1. Square Roots

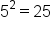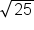Square roots are the most common type of radical used. A square root “unsquares” a number. For example, because 5 squared equals 25, we say the square root of 25 is 5. The square root of 25 is written as square root of 25.

EXAMPLE

Square Root Square Powers
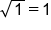
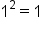
square root of 1 equals 1 1 squared equals 1
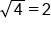
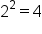
square root of 4 equals 2 2 squared equals 4
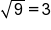
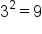
square root of 9 equals 3 3 squared equals 9
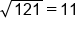
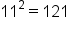
square root of 121 equals 11 11 squared equals 121
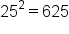
square root of 625 equals 25 25 squared equals 625
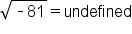
square root of short dash 81 end root equals undefined Not possible

hint
In the last example, square root of short dash 81 end root is undefined, as negatives have no square root. This is because if we square a positive or a negative, the answer will be positive (or zero). Thus, we can only take square roots of non-negative numbers. In another lesson, we define a method we can use to work with and evaluate negative square roots, but for now, we will simply say they are undefined.

Not all numbers have a nice, even square root. For example, if we found 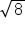square root of 8 on our calculator, the answer would be 2.828427124746190097603377448419... and even this number is a rounded approximation of the square root. Recall that a number such as this is called irrational. Decimal approximations will work in most cases, but you may need the exact value, in which case you will express it using the radical symbol, rather than expressing it as a decimal.

hint
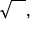When evaluating square roots, look for perfect squares. Perfect square are numbers such as 1, 4, 9, and 16 (they are integers squared). You can also use your calculator's radical button, square root of blank end root comma or apply a 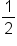1 half exponent. For example: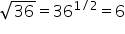 square root of 36 equals 36 to the power of 1 divided by 2 end exponent equals 6

2. Cube Roots

Just like square roots undo squaring a number, cube roots undo cubing a number. For example, because 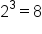2 cubed equals 8, we say that the cube root of 8 is 2. The cube root of 8 is written as 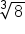cube root of 8 with a 3 as the index of the radical, to indicate a cube root.

EXAMPLE


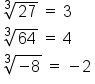
table attributes columnalign left end attributes row cell cube root of 27 space equals space 3 end cell row cell cube root of 64 space equals space 4 end cell row cell cube root of negative 8 end root space equals space minus 2 end cell end table

Notice that the cube root of a negative number results in a real number. This is because a negative number cubed is a negative number. While square roots of negative numbers are non-real numbers, cube roots of negative numbers are real numbers. This pattern holds true for all even roots and odd roots.

big idea
Taking an even root of a negative number leads to a non-real solution because any negative number raised to an even power is positive. However, taking an odd root of a negative number leads to a real number solution because raising a negative number to an odd power results in a negative number.

hint
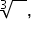When evaluating a cube root, look for perfect cubes. These will result in an integer because perfect cubes are integers cubed. Some examples of perfect cubes are 1, 8, 27, 64, and 125. You can also use your calculator's cube root button, cube root of blank comma or raise to the fractional power 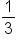1 third. For example: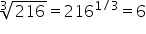 cube root of 216 equals 216 to the power of 1 divided by 3 end exponent equals 6

3. Higher Roots

While square and cube roots are the most common type of radical you will encounter, we can take higher roots of numbers as well: cube roots, fourth roots, fifth roots, etc. Consider this definition of radicals:

formula to know
Definition of Radicals
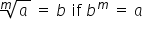
m-th root of a space equals space b space if space b to the power of m space equals space a

The small letter m inside the radical is called the index. It tells us which root we are taking, or which power we are “un-doing.” For square roots, the index is 2. As this is the most common root, the 2 is not usually written.

did you know
The word for root comes from the French mathematician Franciscus Vieta in the late 16th century.

Take a look at several higher roots:

EXAMPLE

Higher Roots Higher Powers
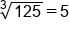
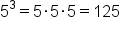
cube root of 125 equals 5 5 cubed equals 5 times 5 times 5 equals 125
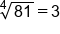
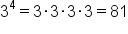
fourth root of 81 equals 3 3 to the power of 4 equals 3 times 3 times 3 times 3 equals 81
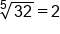
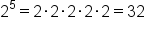
fifth root of 32 equals 2 2 to the power of 5 equals 2 times 2 times 2 times 2 times 2 equals 32
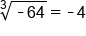
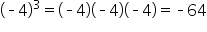
cube root of short dash 64 end root equals short dash 4 open parentheses short dash 4 close parentheses cubed equals open parentheses short dash 4 close parentheses open parentheses short dash 4 close parentheses open parentheses short dash 4 close parentheses equals short dash 64
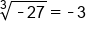
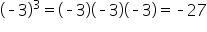
cube root of short dash 27 end root equals short dash 3 open parentheses short dash 3 close parentheses cubed equals open parentheses short dash 3 close parentheses open parentheses short dash 3 close parentheses open parentheses short dash 3 close parentheses equals short dash 27
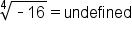
fourth root of short dash 16 end root equals undefined Not possible

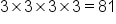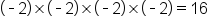This last example is not possible, or is undefined, because if we take any positive or negative number to the fourth power, the answer will be positive (or zero): 3 cross times 3 cross times 3 cross times 3 equals 81 or open parentheses short dash 2 close parentheses cross times open parentheses short dash 2 close parentheses cross times open parentheses short dash 2 close parentheses cross times open parentheses short dash 2 close parentheses equals 16. Thus, we can only take the fourth roots of non-negative numbers.

hint
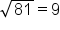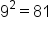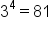We must be careful of a few things as we work with higher roots. First, it's important not to forget to check the index on the root. square root of 81 equals 9 but fourth root of 81 space equals space 3. This is because 9 squared equals 81 and 3 to the power of 4 equals 81. Another thing to watch out for is negative values under roots. We can take an odd root of a negative number because a negative number raised to an odd power is still negative. However, we cannot take an even root of a negative number because a negative number raised to an even power is positive.

summary
There are several methods you can use to evaluate radicals, or roots, such as square roots, cube roots, and higher roots (fourth roots, fifth roots, etc.). If you use a calculator to evaluate the radical, you first type in the radical button and then you type in the number. If your calculator does not have the necessary nth root button, you're going to use a fractional exponent and type it in as caret, open parentheses, one divided by n, close parentheses. And again, your n number is just the index of your radical. And finally, the nth root of a negative number will not evaluate to be a real number if n is even⁠—like square root⁠—but it will evaluate to be a real number if n is odd⁠—like the cubed root.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Definition of Radicals

m-th root of a equals b space i f space b to the power of m equals a

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.