Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Evaluate Piecewise Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how a piecewise function is defined and how it is evaluated. Specifically, this lesson will cover:

Table of Contents

1. Uses of Piecewise Functions in the Real World

A job pays $24 per hour as long as an employee works at most 40 hours in a week. If an employee works more than 40 hours, they still get $24 for each of the first 40 hours, but they also get $36 for every extra hour beyond 40.

How would we calculate an employee’s earnings?

There are two rules, depending on the number of hours worked:

40 hours or less Earnings = 24 times (Hours)
More than 40 hours Earnings = 24 times 40 + 36 times (Extra Hours)

If the goal is to calculate several employees’ earnings, a piecewise function is needed since there are two rules to calculate the same output (earnings).

2. Defining Piecewise Functions

Let’s take this situation and try to represent it mathematically. Let x = the number of hours an employee works in a week.

Each entry in the table above can be translated into a mathematical statement involving the variable x.

Mathematical Statement Statement in Words
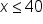
x less or equal than 40 “40 hours or less”
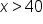
x greater than 40 “More than 40 hours”
Earnings = 24x Earnings = 24 times (Hours)
Earnings = 24(40) + 36(x – 40)

Note: “x – 40” is the number of extra hours. If someone works more than 40 hours, then you subtract 40 from the hours they worked to get the number of extra hours. 		Earnings = 24*40 + 36 times (Extra Hours)

In this situation, notice also that the weekly earnings depend on the number of hours worked. That is, the earnings is a function of the number of hours worked. Using function notation, let 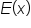E open parentheses x close parentheses represent the earnings after x hours.

Since there are two rules to find 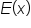E open parentheses x close parentheses, we can express 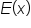E open parentheses x close parentheses as a piecewise function. Here is how it would be written:

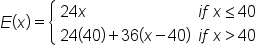
E open parentheses x close parentheses equals open curly brackets table attributes columnalign left center end attributes row cell 24 x end cell cell i f space x less or equal than 40 end cell row cell 24 open parentheses 40 close parentheses plus 36 open parentheses x minus 40 close parentheses end cell cell i f space x greater than 40 end cell end table close

This function isn’t quite accurate for the following reasons:
  • x cannot be negative (the number of hours worked cannot be negative).
  • x cannot be more than 168 (# hours in a week).
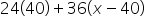The expression 24 open parentheses 40 close parentheses plus 36 open parentheses x minus 40 close parentheses is not in its final form because it can be simplified.

After addressing these things, the function could be written as:

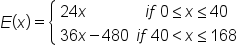
E open parentheses x close parentheses equals open curly brackets table attributes columnalign left center end attributes row cell 24 x end cell cell i f space 0 less or equal than x less or equal than 40 end cell row cell 36 x minus 480 end cell cell i f space 40 less than x less or equal than 168 end cell end table close

term to know
Piecewise Function
Assigns an input to an output, but the rule used to determine the output depends on the value of the input.

3. Evaluating Piecewise Functions

The purpose of the function we built in the previous section is to calculate earnings for employees. In order to do so, remember that the input determines which rule is used:

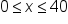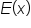If 0 less or equal than x less or equal than 40, then use 24x to compute E open parentheses x close parentheses.
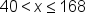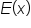If 40 less than x less or equal than 168, then use 36x - 480 to compute E open parentheses x close parentheses.

EXAMPLE

Let’s use the function to compute earnings for several employees:

Employee, Hours Hours written in terms of x Which Rule Should We Use? Calculate E  (x  )
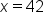
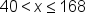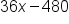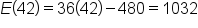
Holly, 42 hours x equals 42 Since 42 satisfies 40 less than x less or equal than 168, use 36 x minus 480. E open parentheses 42 close parentheses equals 36 open parentheses 42 close parentheses minus 480 equals 1032
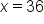
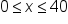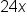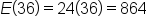
George, 36 hours x equals 36 Since 36 satisfies 0 less or equal than x less or equal than 40, use 24 x. E open parentheses 36 close parentheses equals 24 open parentheses 36 close parentheses equals 864
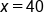
Israel, 40 hours x equals 40 Since 40 satisfies 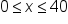0 less or equal than x less or equal than 40, use 24 x. E open parentheses 40 close parentheses equals 24 open parentheses 40 close parentheses equals 960
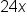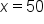
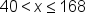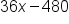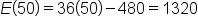
Savannah, 50 hours x equals 50 Since 50 satisfies 40 less than x less or equal than 168, use 36 x minus 480. E open parentheses 50 close parentheses equals 36 open parentheses 50 close parentheses minus 480 equals 1320

Conclusion: Holly earned $1032, George earned $864, Israel earned $960, and Savannah earned $1320.

try it
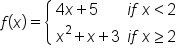
Let f open parentheses x close parentheses equals open curly brackets table attributes columnalign left center end attributes row cell 4 x plus 5 end cell cell i f space x less than 2 end cell row cell x squared plus x plus 3 end cell cell i f space x greater or equal than 2 end cell end table close

Evaluate f (-3), f (5), and f (2).
f open parentheses short dash 3 close parentheses equals 4 open parentheses short dash 3 close parentheses plus 5 equals short dash 7 Use the first rule since short dash 3 less than 2.
f open parentheses 5 close parentheses equals 5 squared plus 5 plus 3 equals 33 Use the second rule since 5 greater or equal than 2.
f open parentheses 2 close parentheses equals 2 squared plus 2 plus 3 equals 9 Use the second rule since 2 greater or equal than 2.

summary
In this lesson, you learned that whenever a situation involves more than one rule for computing an output, it can be represented mathematically by a piecewise function. A piecewise function assigns an input to an output, where the rule used to determine the output depends on the value of the input. You began the lesson by exploring uses of piecewise functions in the real world, then learned how to define piecewise functions by taking entries in a table and translating them into a mathematical statement involving the variable x. Lastly, you learned how to evaluate piecewise functions by calculating earnings for employees, applying the appropriate rule, determined by the input, to calculate the output (earnings).

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Piecewise Function

Assigns an input to an output, but the rule used to determine the output depends on the value of the input.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.