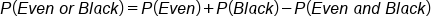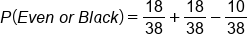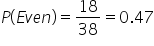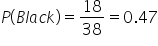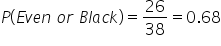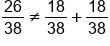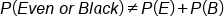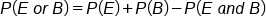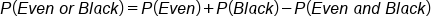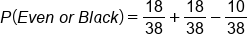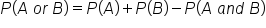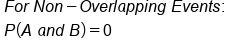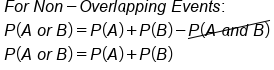EXAMPLE
Consider the roulette wheel.

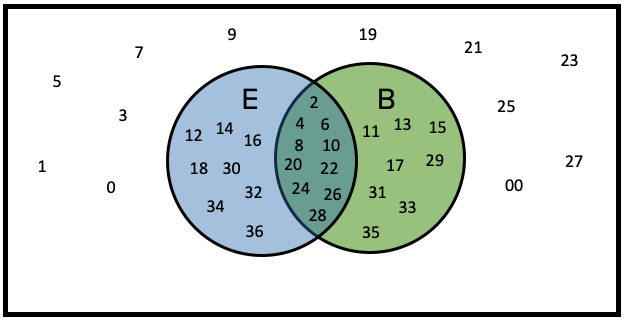
What's the probability of getting an even number on a roulette wheel? This is not an “or” probability. We're simply finding the probability of spinning an even number. Looking just in the even circle, 18 numbers are even on the roulette wheel, out of 38 sectors. Zero and double zero don't count as even.
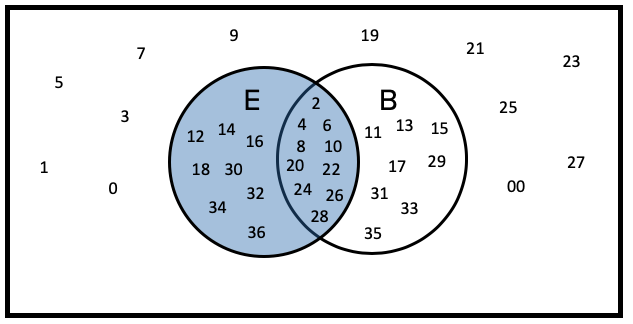
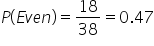
What is the probability of black on the roulette wheel? It's the same idea. Look in the circle that represents black numbers; it's also 18 out of 38, coincidentally the same number.
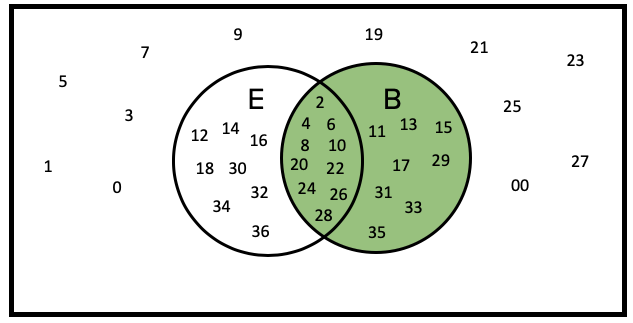
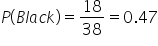
What's the probability of even
or black? Count up the numbers that are in either even or black. You get 26 out of the 38.
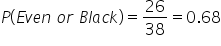
Now the question is, why is the probability of E or B not equal to the probability of E plus probability of B?
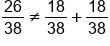
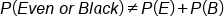
When you add the probability of an even number (18/38) plus the probability of a black number (18/38), you might expect to get 36/38, but you don't—you get 26/38. The reason for the miscount is because some of the numbers were counted twice. Some were counted as even, and some were counted again as being black, whereas we should only have counted them once.
Which values were double counted? It was the numbers that were black
and even. You make this adjustment by first adding P(black) to P(even), then subtract out the things that got double counted P(black and even), so they are only counted once. The double counts were the numbers that were both black and even, represented in the overlap of the Venn diagram.
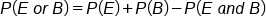
This represents the “either/or” probability for overlapping events: The probability of E or B is equal to the probability of E plus the probability of B, minus the probability of E and B.
Let's illustrate this concept by boxing the probability of all even numbers and circling the probability of B numbers.
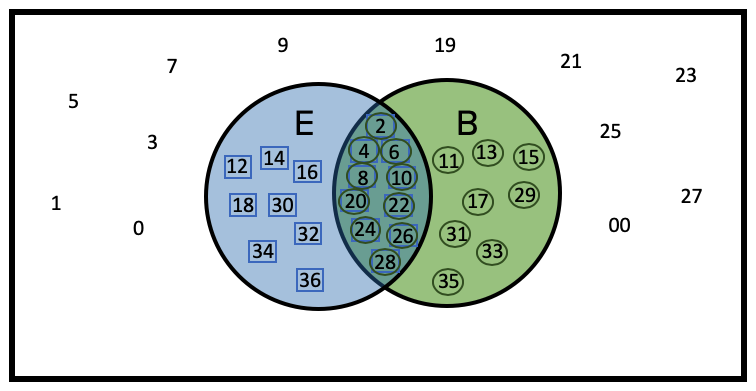
Notice how the numbers in the middle got both circled and boxed. You only want to count them once. But when we include the numbers with the E’s and also with the B’s, they were counted twice. Remove one of those markings to only count everything once.