Table of Contents |
Using the sum of angles identities, we can establish identities that give values of 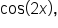
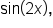 and
and 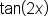 in terms of trigonometric functions of x.
in terms of trigonometric functions of x.
Starting with the cosine, write 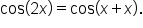
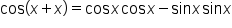
|
Apply the sum of angles identity for the cosine of a sum of angles. |
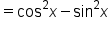
|
Simplify. |
Thus, 
Notice that the identity contains 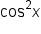 and
and 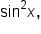 which are related by the Pythagorean identity
which are related by the Pythagorean identity 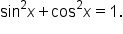
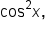 we have
we have 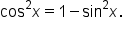
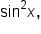 we have
we have 
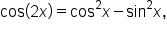 we are able to get alternate formulas for
we are able to get alternate formulas for 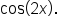
First, if we replace 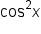 with
with 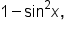 we have:
we have:
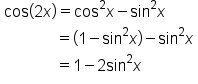
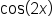 in terms of
in terms of 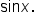
Similarly, if we replace 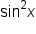 with
with 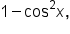 we have yet another version of
we have yet another version of 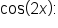
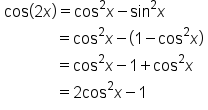
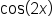 when
when  is known.
is known.
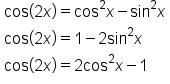
To establish a double-angle identity for sine, write 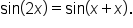
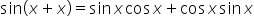
|
Apply the identity for the sine of a sum of angles. |
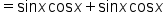
|
Reverse the factors in the second term. |
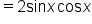
|
Simplify. |
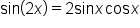
Lastly, to find a double-angle identity for tangent, write 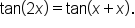
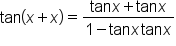
|
Apply the identity for the tangent of a sum of angles. |
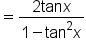
|
Simplify. |
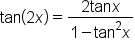
EXAMPLE
Given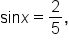 where
where 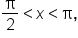 find the exact values of
find the exact values of 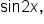
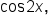 and
and 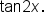
 Since
Since  is not given but
is not given but 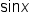 is known, use a Pythagorean identity to find
is known, use a Pythagorean identity to find 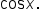
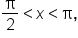 we know that
we know that 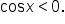
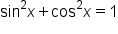
|
This is the Pythagorean identity. |
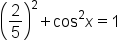
|
Replace 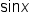 with with 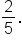
|
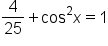
|
Simplify. |
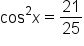
|
Subtract  from both sides. from both sides.
|
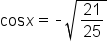
|
Apply the square root property. Since 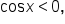 only the negative solution is considered. only the negative solution is considered.
|
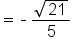
|
Simplify. |
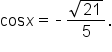
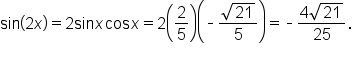
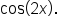
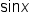 is given, it is most convenient to use the identity
is given, it is most convenient to use the identity 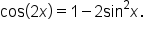
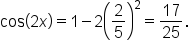
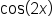 could be used. You would get the same answer; it just might require more steps.
could be used. You would get the same answer; it just might require more steps.
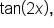 the double angle identity requires the value of
the double angle identity requires the value of 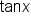 to be known. While we could find this, remember also that
to be known. While we could find this, remember also that 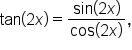 and
and 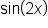 and
and 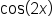 have already been calculated.
have already been calculated.
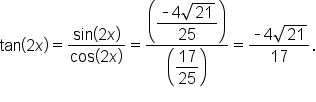
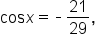 where
where 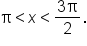
We can also use double-angle identities to prove trigonometric identities.
EXAMPLE
Prove the identity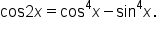
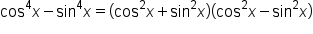
|
Factor as a difference of squares. |
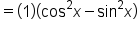
|
Apply the Pythagorean identity, 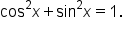
|
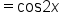
|
Apply the cosine of a double angle identity, 
|
Power-reducing identities are used to write even powers of sine, cosine, and tangent as trigonometric functions with smaller powers. These identities are very useful, particularly in calculus.
Recall that we had the identities  and
and 
Solving the first equation for 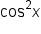 gives
gives 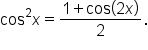
Solving the second equation for 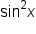 gives
gives 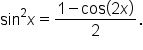
Also, since 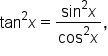 we have
we have 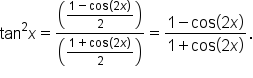
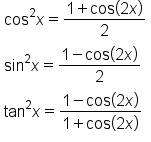
EXAMPLE
Use power-reducing identities to write an equivalent expression for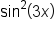 with no exponent larger than 1.
with no exponent larger than 1.
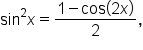 replace x with 3x.
replace x with 3x.
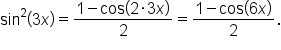
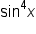 as an expression with no powers.
as an expression with no powers.
EXAMPLE
Use power-reducing identities to write an equivalent expression for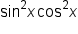 with no exponent larger than 1.
with no exponent larger than 1.
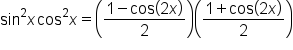
|
Use the power-reducing identities. |
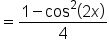
|
Perform the multiplication and simplify. |
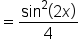
|
Apply a Pythagorean identity. |
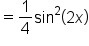
|
Rewrite with 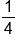 in front. in front.
|
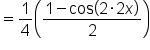
|
Apply a power-reducing identity. |
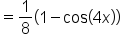
|
Simplify. |
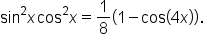
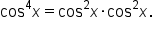
Bicycle ramps made for competition must vary in height depending on the skill level of the competitors. For advanced competitors at one particular event, the angle formed by the ramp and the ground should be the acute angle 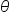 such that
such that 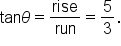
For novices at this same event, the angle is divided in half. Recalling that 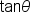 gives the steepness (slope) of a line that passes through the origin, what is the steepness of the ramp for novices? That is, what is the value of
gives the steepness (slope) of a line that passes through the origin, what is the steepness of the ramp for novices? That is, what is the value of 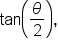 and can we get this value knowing that
and can we get this value knowing that 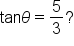 We’ll be able to answer this question, and others, by establishing half-angle identities.
We’ll be able to answer this question, and others, by establishing half-angle identities.
To start, consider the power-reducing identities:
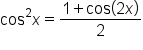
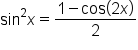
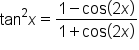
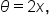 then
then 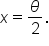 We now have:
We now have:
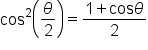
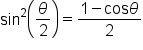
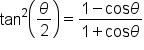
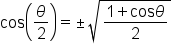
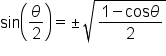
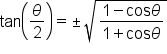
 ” is determined by the quadrant in which
” is determined by the quadrant in which  terminiates.
terminiates.
These identities collectively are known as the half-angle identities.
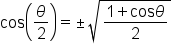
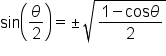
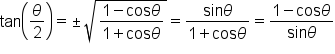
 ” is determined by the quadrant in which
” is determined by the quadrant in which  terminates.
terminates.Just like the other identities we have used, the half-angle identities can be used to find exact values of angles that are half the value of a special angle.
EXAMPLE
Use a half-angle identity to find the exact value of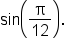
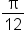 is equivalent to
is equivalent to 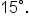
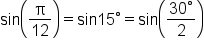
|
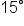 is half of is half of 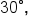 and and 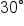 is a special angle. is a special angle.
|
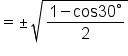
|
Apply the appropriate half-angle identity. |
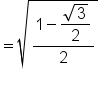
|
Replace 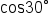 with with  Use the positive square root since 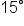 terminates in quadrant I, and all trigonometric functions have positive values in quadrant I. terminates in quadrant I, and all trigonometric functions have positive values in quadrant I.
|
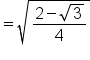
|
Inside the radical, multiply the numerator and denominator by 2. |
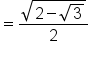
|
Take the square root of the numerator and denominator. |
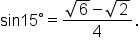 While not obvious, both of these answers are equivalent.
While not obvious, both of these answers are equivalent.
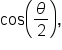 given
given 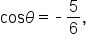 where
where 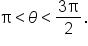
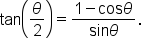
EXAMPLE
Given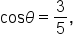 where
where 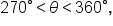 find the exact value of
find the exact value of 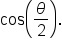
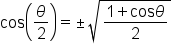
|
This is the half-angle identity. |
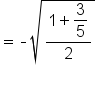
|
Since 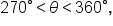 it follows that it follows that 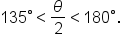 Then, Then, 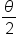 terminates in quadrant II, which means terminates in quadrant II, which means 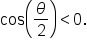
|
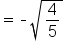
|
Simplify under the radical. |
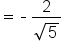
|
Simplify the square root. |
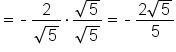
|
Rationalize the denominator. |
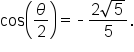
Now, let’s answer the question about the bicycle ramp from earlier.
EXAMPLE
Given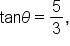 where
where 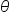 is acute, find the exact value of
is acute, find the exact value of 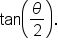
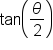 require us to know
require us to know 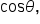 we’ll start by finding
we’ll start by finding 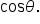
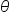 is acute, there are two methods that could be used:
is acute, there are two methods that could be used:
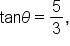 the side opposite
the side opposite 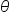 has length 5, and the side adjacent to
has length 5, and the side adjacent to 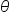 has length 3.
has length 3.
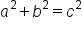
|
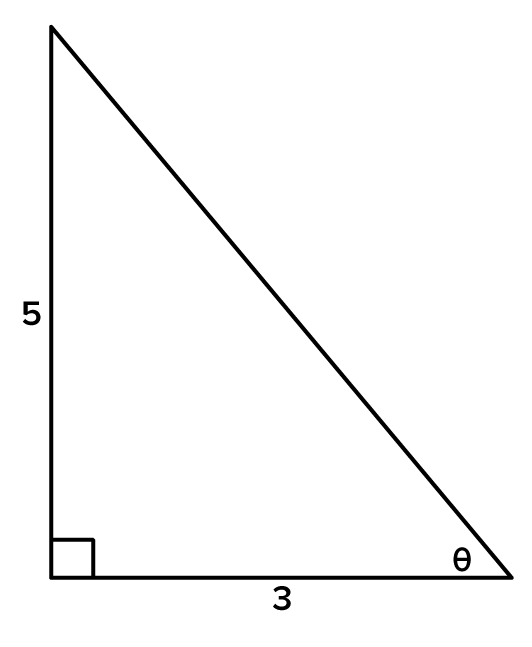
This is the Pythagorean theorem. |
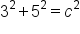
|
The legs are 3 and 5, so one of them is  and the other is b. and the other is b.
|
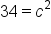
|
Simplify. |
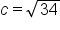
|
Apply the square root principle, Since c is the length of a side, only the positive solution is considered. |
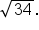
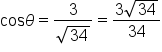 after rationalizing the denominator.
after rationalizing the denominator.
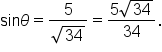
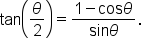
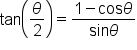
|
This is a half-angle identity. |
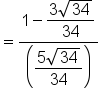
|
Replace 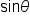 and and 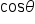 with their values. with their values.
|

|
Multiply the numerator and denominator by 34 to simplify the complex fraction. |
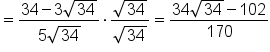
|
Rationalize the denominator. |
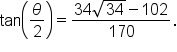 For context, this is approximately 0.566, which is approximately one third of the steepness of the original ramp whose slope is
For context, this is approximately 0.566, which is approximately one third of the steepness of the original ramp whose slope is 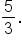
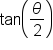 given
given 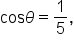 where
where 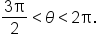
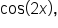
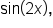 and
and 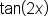 in terms of trigonometric functions of x. You can also use double-angle identities to prove trigonometric identities. You also learned how to use power-reducing identities to write even powers of sine, cosine, and tangent as trigonometric functions with smaller powers. Finally, you learned how to use half-angle identities to find exact values of angles that are half the value of a special angle. In summary, double-angle identities, power-reducing identities, and half-angle identities all are used in conjunction with other identities to evaluate expressions, simplify expressions, and verify trigonometric identities.
in terms of trigonometric functions of x. You can also use double-angle identities to prove trigonometric identities. You also learned how to use power-reducing identities to write even powers of sine, cosine, and tangent as trigonometric functions with smaller powers. Finally, you learned how to use half-angle identities to find exact values of angles that are half the value of a special angle. In summary, double-angle identities, power-reducing identities, and half-angle identities all are used in conjunction with other identities to evaluate expressions, simplify expressions, and verify trigonometric identities.
SOURCE: THIS WORK IS ADAPTED FROM PRECALCULUS BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/BOOKS/PRECALCULUS/PAGES/1-INTRODUCTION-TO-FUNCTIONS