Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Domain and Range of Square Root and Rational Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to determine the domain and range of a square root function. Specifically, this lesson will cover:

Table of Contents

1. Domain and Range

In a function, the domain is the set of all possible input values. In other words, it represents all values that the independent variable (usually x) is allowed to take on in order to return a value for the function. The range is the set of all possible output values (usually y); or values that the function will have, depending on all of the possible input values.

When a function has no restrictions on its domain, it is continuous from negative infinity to positive infinity along the x-axis. If the range also has no restrictions, then on one end, the graph tends towards negative infinity, and on the other end, it tends towards positive infinity. Below is the graph of a polynomial that has no domain or range restrictions:

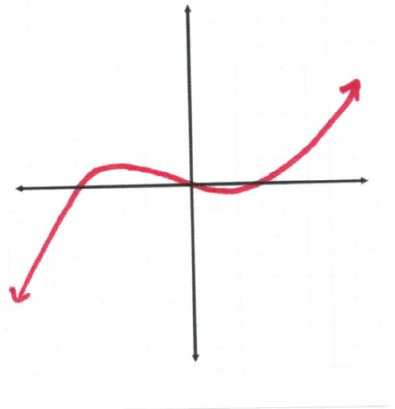
A graph with an x-axis and a y-axis intersecting at the origin. A curve starts in the third quadrant at the bottom left, extends into the second quadrant, rises slightly, then dips again, passes through the origin into the fourth quadrant, and finally rises steeply into the first quadrant toward the top right.

When talking about domain restrictions, the two common cases:

  • When there is an expression underneath a square root (or other even roots) because the expression under the even root must be non-negative
  • When there is a denominator with a variable in it (as is the case with rational functions) because the denominator must not equal zero
We will use these ideas in finding domain restrictions below.

terms to know
Domain
The set of input values of a function or relation.
Range
The set of output values of a function or relation.

2. Domain and Range of Square Root Functions

The find the domain range, we need to identify restrictions to both the domain and range.

EXAMPLE

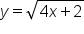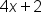Find the domain and range of y equals square root of 4 x plus 2 end root.

Since this is a square root function, we need to set the expression underneath the radical, 4 x plus 2, greater than or equal to zero, and solve the inequality for x:

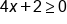
4 x plus 2 greater or equal than 0 Subtract 2 from both sides
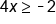
4 x greater or equal than short dash 2 Divide by 4
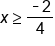
x greater or equal than fraction numerator short dash 2 over denominator 4 end fraction Simplify
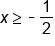
x greater or equal than short dash 1 half Our solution

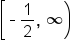This means that the function is defined for any x-value greater than or equal to negative one-half. We can write this as open square brackets short dash 1 half comma space infinity close parentheses. We can see this below when we graph the function. If the inequality had no solution (that is, no values of x for which the expression is less than zero), then the domain has no restrictions.

Since this function does not have a denominator, we can simply examine the graph of this function to describe its range:

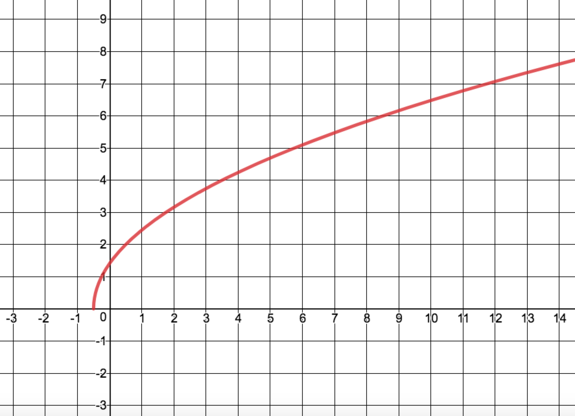
A graph with an x-axis ranging from −3 to 14 and a y-axis ranging from −3 to 9. A curve starts from the point (−0.5, 0) in the second quadrant, passes through the point (0, 1.4), and extends into the first quadrant beyond the point (14, 7.7). The curve rises sharply, then rises more slowly as x increases.

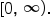
We see that as x gets larger and larger, the function heads towards positive infinity (even if rather slowly). On the other side of the graph, however, the function never falls below the x-axis. Therefore, the range is from zero to positive infinity. Since the function can have the exact value of zero, we can write this as left square bracket 0 comma space infinity right parenthesis.

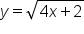For the function y equals square root of 4 x plus 2 end root, the domain is 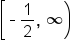open square brackets short dash 1 half comma space infinity close parentheses and the range is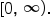 left square bracket 0 comma space infinity right parenthesis.

big idea
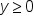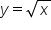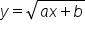For square-root functions, the range is any value of y such that y greater or equal than 0. It is not possible for a square root to result in a negative value, so the functions in the form y equals square root of x or y equals square root of a x plus b end root will always be greater than or equal to zero.

3. Domain and Range of Rational Functions

With rational functions, the domain restrictions are x-values that make the denominator equal to zero. So we need to set the denominator equal to zero and solve for x. This will give us x-values to exclude from the domain:

EXAMPLE

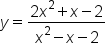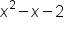Find the domain and range of y equals fraction numerator 2 x squared plus x minus 2 over denominator x squared minus x minus 2 end fraction.

To find the domain restrictions, set the denominator x squared minus x minus 2 equal to zero and solve for x.

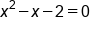
x squared minus x minus 2 equals 0 Factor the quadratic expression
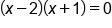
open parentheses x minus 2 close parentheses open parentheses x plus 1 close parentheses equals 0 Set each factor to zero
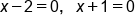
x minus 2 equals 0 comma space space space x plus 1 equals 0 Evaluate each factor
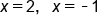
x equals 2 comma space space space x equals short dash 1 Our solutions

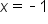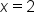This means that the domain of the rational function is all x-values EXCEPT x equals short dash 1 and x equals 2.

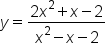If we are able to rewrite the denominator in factored form, it is easier to see the solutions. In the above example, the function y equals fraction numerator 2 x squared plus x minus 2 over denominator x squared minus x minus 2 end fraction can be written as 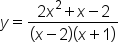y equals fraction numerator 2 x squared plus x minus 2 over denominator left parenthesis x minus 2 right parenthesis left parenthesis x plus 1 right parenthesis end fraction. Setting each factor in the denominator to zero will give the values of the restrictions. And as we said above, if the equation has no solution (that is, no values of x that make the denominator equal to zero), then the domain has no restrictions.

To find the range, we can examine the graph of this function, too:

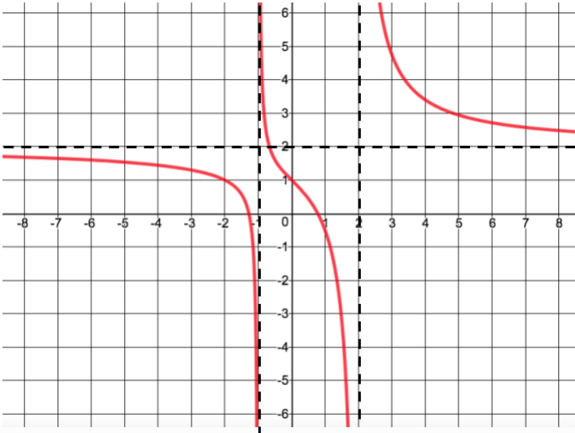
A graph with an x-axis ranging from −8 to 8 and a y-axis ranging from −6 to 6. The graph has a horizontal dashed line, two vertical dashed lines, and three curves. The horizontal dashed line passes through y equals 2, and the two vertical dashed lines pass through x equals −1 and x equals 2. One curve starts in the second quadrant below the horizontal dashed line, passes through the point (−2, 1), and moves downward into the third quadrant, almost overlapping the dashed line x equals −1. The second curve starts in the second quadrant from the upper limit of the y-axis, moves downward along the dashed line x equals −1, then bends to pass through the points (0, 1) and (1, −0.5), and extends downward into the fourth quadrant close to the dashed line x equals 2. The third curve is between the dashed lines x equals 2 and y equals 2. It starts in the first quadrant, moves downward close to the dashed line x equals 2, and then opens rightward to extend above the line y equals 2 by passing through the point (5, 3). These curves extend toward infinity while never touching the origin.

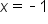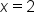We can see that the domain restrictions are represented with the vertical asymptotes in this function, at x equals short dash 1 and x equals 2.

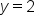We also see a horizontal asymptote, which can be found by dividing the leading coefficients in the numerator and denominator of the function. So the line is y equals 2. We may be tempted to say that 2 is excluded from the range, because as the function gets more and more negative, and more and more positive, the value of the function approaches, but never reaches 2. However, in between our vertical asymptotes, we see that function actually does at one point have a value of 2. So we can then say that the range of this function is all real numbers,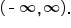 left parenthesis short dash infinity comma infinity right parenthesis.

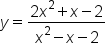For the function y equals fraction numerator 2 x squared plus x minus 2 over denominator x squared minus x minus 2 end fraction, the domain is all values of x EXCEPT for -1 and 2, and the range is all real numbers.

summary
In a function, the domain is the set of all possible input values of the function and the range is the set of all possible output values of the function. To find the domain and range of square root functions, you need to consider domain restrictions because the square root of a negative value is undefined. To find the domain and range of rational functions, you need to consider the domain restrictions because division by 0 leaves the function undefined.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Domain

The set of input values of a function or relation.

Range

The set of output values of a function or relation.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.