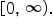In this lesson, you will explore the domain and range of a function. This is very important since the domain and range collectively tell us the possible inputs and outputs of a function. Specifically, this lesson will cover:
1. Finding the Domain of a Function Defined by an Equation
First, recall the definitions of domain and range. The domain of a function is the set of all possible values that can be used as inputs to a function. The range of a function is the set of all possible outputs that can be obtained from a function.
First, we’ll focus on finding the domain of a function when given its equation. This is mostly straightforward for functions having certain forms.
Given an equation of a function, the domain can be determined by a variety of factors.
- Does the function have a variable in the denominator? If so, exclude any values for which the denominator is equal to 0.
- Does the function involve an even root (square root, 4th root, etc.)? If so, only include values for which the radicand is nonnegative.
- If there are no restrictions on the input value, then assume the domain is the set of all real numbers.
-
EXAMPLE
Find the domain of the function
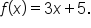
Things to note:
-
 contains no fraction with a variable denominator.
contains no fraction with a variable denominator.
-
 contains no radicals.
contains no radicals.
There are no restrictions on what numbers can be substituted for
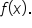
Thus, the domain of

is the set of all real numbers. Using interval notation, this is written as

-
In this course and in calculus, interval notation is usually the preferred way to express domains and ranges of functions. In all future examples, domains will be expressed using interval notation.
-
Consider the function
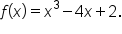
-
EXAMPLE
Find the domain of the function
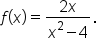
The function has a variable denominator. This means that

is undefined when
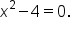
Solve this equation to find the specific values of
x.
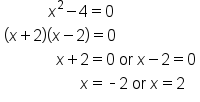
This means that

is undefined when
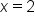
or when
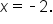
Thus, the domain is the set of all real numbers except
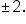
This could be written as
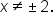
Using interval notation, the domain is written as
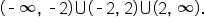
-
Consider the function
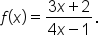
Now we’ll look at functions that contain radicals with even roots (square roots, 4th roots, etc.).
-
EXAMPLE
Find the domain of the function
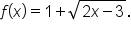
Express the domain using interval notation.
When only real numbers are considered, recall that only square roots of nonnegative numbers are defined. This means that the domain of this function is the set of values of
x for which
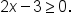
Now, solve the inequality:
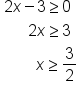
Using interval notation, the inequality
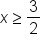
is written as
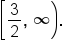
Thus, the domain of the function is
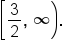
-
Consider the function
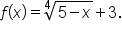
Since we just looked at functions that contain radicals with even roots, we’ll now examine functions that contain radicals with odd roots.
-
EXAMPLE
Find the domain of the function
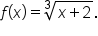
Express the domain using interval notation.
Recall that the cube root (or any odd root of a number) can be applied to any real number (positive, zero, or negative). Since the radicand has no restrictions on it as well, the domain of

is the set of all real numbers. Using interval notation, this is expressed as

-
Consider the function
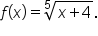
Here is an example that combines a few ideas.
-
EXAMPLE
Determine the domain of the function
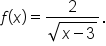
First, notice that the function contains a square root. The square root is defined for values of
x where the radicand is nonnegative:
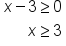
Also, the radical is in the denominator. This means that the radicand cannot equal 0. This means that
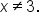
Pulling these together, the domain of the function is the set of all values for which
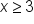
and
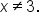
More simply stated, the domain is
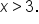
Written using interval notation, the domain is expressed as
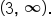
It is not always convenient to find the domain of a function given only its equation. The graph of the function can be very useful in determining both the domain and the range of a function.
-
- Domain
- The set of all possible values that can be used as inputs to a function.
- Range
- The set of all possible outputs that can be obtained from a function.
2. Finding Domain and Range From Graphs
Recall that the graph of a function is a visual representation of all solutions to an equation.
Recall also that the domain is the set of all possible inputs of a function. On a graph, these are represented as values on the x-axis. Likewise, the range is the set of all output values of a function, which are shown as values on the y-axis.
For instance, consider the graph shown below.
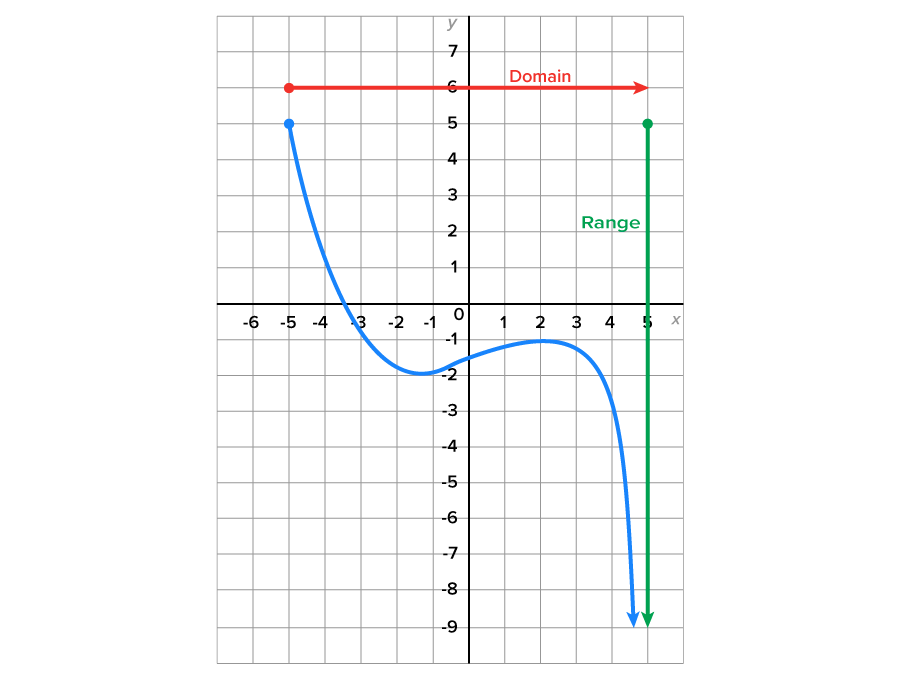
- Looking at the graph from left to right, the smallest x-value that is represented on the graph is -5, and the graph appears to continue to the right indefinitely. Thus, the domain of the function is
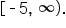
- Observe that the highest point on the graph is
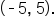 Looking at the graph vertically, all y-values that are lower than 5 are also represented on this graph. Thus, the range of the function is
Looking at the graph vertically, all y-values that are lower than 5 are also represented on this graph. Thus, the range of the function is 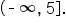
-
EXAMPLE
Determine the domain and range of the function whose graph is shown below.
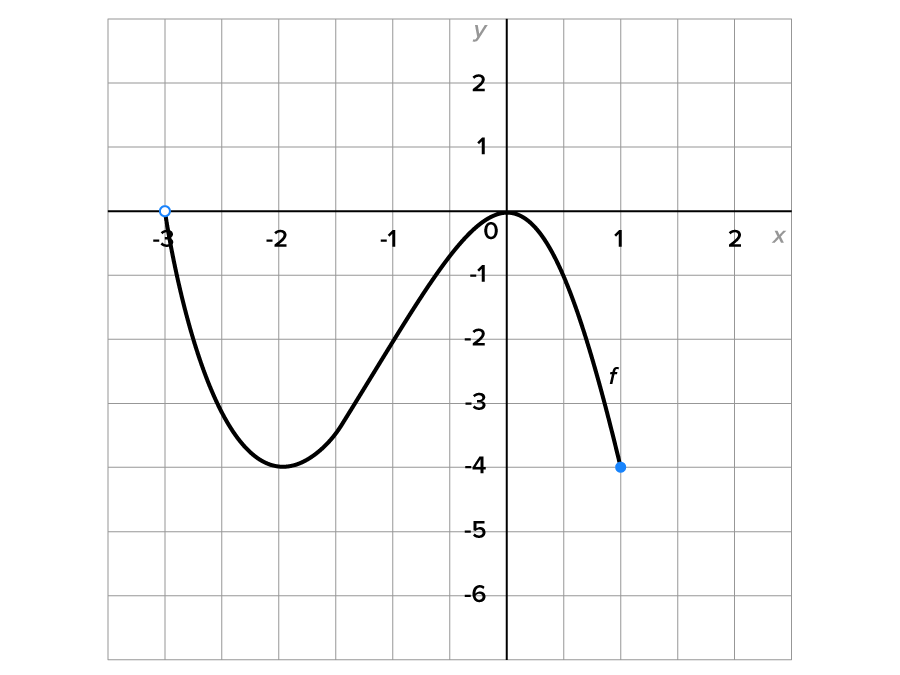
Looking at the graph from left to right, notice that the leftmost point,
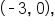
is an open circle. This means that
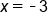
is not included. The rightmost point on the graph is
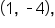
which is solid, meaning it is included. The domain of this function is
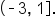
Looking at the graph vertically, the lowest y-value represented on the graph is -4 (located at
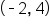
and
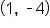
), while the highest y-value is 0 (located at
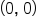
). The range of this function is

-
Determine the domain and range of the function whose graph is shown below:
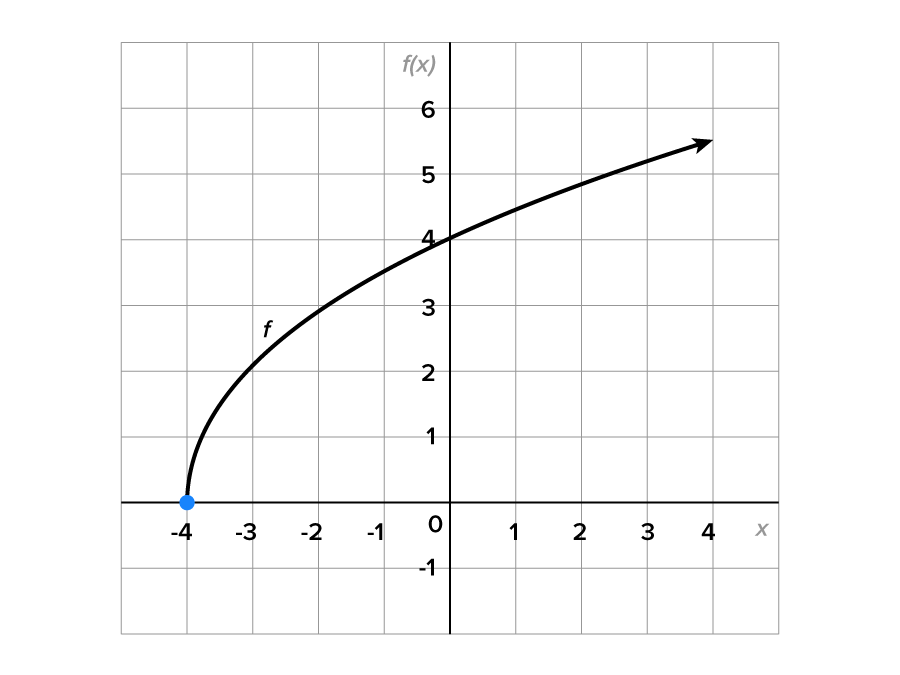
-
In manufacturing, suppose the total cost of producing
x pounds of a certain material is estimated by the function
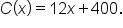
From what we know about the domain already, it should be the set of all real numbers. However, in this situation, it makes no sense for
x to be a negative number, since
x is the number of pounds. Therefore, a more sensible domain is
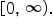
The moral of the story is that the domain is determined by two things: the function itself, and the context of the function (if any is given).
In this lesson, you recalled that the domain and range provide useful information about a function in that they tell us the sets of numbers that can be used for inputs and outputs, respectively. You learned how to find the domain of a function defined by an equation using interval notation, determined by a variety of factors such as whether the function has a variable in the denominator or involves an even index root, and if there are no restrictions on the input value. Recalling that the graph of a function is a visual representation of all solutions to an equation, you also learned how to find domain and range from graphs, where the domain is represented as values on the x-axis as you scan from left to right, and the range is shown as values on the y-axis as you scan from bottom to top. Keep in mind that special care needs to be taken in real-life situations where certain values of x (or y) do not make sense in the situation (for instance, a negative length, or a fractional number of items).
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM 1) CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES. 2) OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.
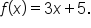
 contains no fraction with a variable denominator.
contains no fraction with a variable denominator. contains no radicals.
contains no radicals. 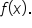 Thus, the domain of
Thus, the domain of  is the set of all real numbers. Using interval notation, this is written as
is the set of all real numbers. Using interval notation, this is written as 
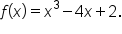
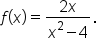
 is undefined when
is undefined when 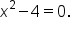 Solve this equation to find the specific values of x.
Solve this equation to find the specific values of x.
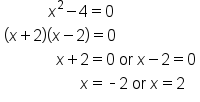
 is undefined when
is undefined when 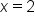 or when
or when 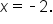
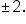 This could be written as
This could be written as 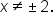 Using interval notation, the domain is written as
Using interval notation, the domain is written as 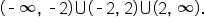
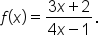
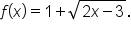 Express the domain using interval notation.
Express the domain using interval notation.
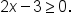
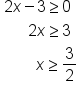
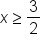 is written as
is written as 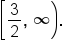 Thus, the domain of the function is
Thus, the domain of the function is 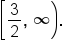
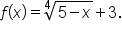
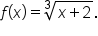 Express the domain using interval notation.
Express the domain using interval notation.
 is the set of all real numbers. Using interval notation, this is expressed as
is the set of all real numbers. Using interval notation, this is expressed as 
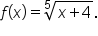
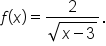
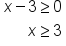
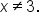
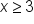 and
and 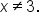 More simply stated, the domain is
More simply stated, the domain is 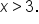
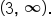

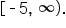
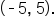 Looking at the graph vertically, all y-values that are lower than 5 are also represented on this graph. Thus, the range of the function is
Looking at the graph vertically, all y-values that are lower than 5 are also represented on this graph. Thus, the range of the function is 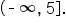

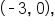 is an open circle. This means that
is an open circle. This means that 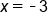 is not included. The rightmost point on the graph is
is not included. The rightmost point on the graph is 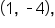 which is solid, meaning it is included. The domain of this function is
which is solid, meaning it is included. The domain of this function is 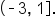
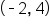 and
and 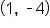 ), while the highest y-value is 0 (located at
), while the highest y-value is 0 (located at 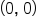 ). The range of this function is
). The range of this function is 

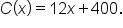 From what we know about the domain already, it should be the set of all real numbers. However, in this situation, it makes no sense for x to be a negative number, since x is the number of pounds. Therefore, a more sensible domain is
From what we know about the domain already, it should be the set of all real numbers. However, in this situation, it makes no sense for x to be a negative number, since x is the number of pounds. Therefore, a more sensible domain is