Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Distance Between Two Points

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to find the distance between two points on a number line and also on the xy-plane. Specifically, this lesson will cover:

Table of Contents

1. The Distance Between Two Numbers on a Number Line

Suppose you want to calculate the distance between two locations on a number line, as shown below.

A numbered line divided into segments that has two marked points labeled ‘a’ and ‘b’ and a highlighted portion starting at ‘a’ and ending at ‘b’, representing that b is greater than a.

The distance between these two points is b minus a comma but that is assuming that b is larger than 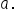a.

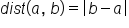In general, just so we don’t have to worry about which number is larger, the distance between two numbers a and b is d i s t open parentheses a comma space b close parentheses equals open vertical bar b minus a close vertical bar. The absolute value is used to ensure that the result is not negative.

formula to know
Distance on a Number Line
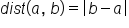
d i s t open parentheses a comma space b close parentheses equals open vertical bar b minus a close vertical bar

try it
Find the distance between a and b in each example below.
What is the distance when a = 13 and b = 5?
The distance between 13 and 5 is 8.

d i s t left parenthesis 13 comma space 5 right parenthesis equals open vertical bar 5 minus 13 close vertical bar equals open vertical bar short dash 8 close vertical bar equals 8
What is the distance when a = -21 and b = 9?
The distance between -21 and 9 is 30.

d i s t left parenthesis short dash 21 comma space 9 right parenthesis equals open vertical bar 9 minus open parentheses short dash 21 close parentheses close vertical bar equals open vertical bar 9 plus 21 close vertical bar equals open vertical bar 30 close vertical bar equals 30

term to know
Distance
The length of a line segment between two points.

2. The Distance Between Two Points in the xy-Plane

The following image shows two points, P and Q, and the distance between them in the xy-plane, d. Let's find a formula for the distance between these two points.

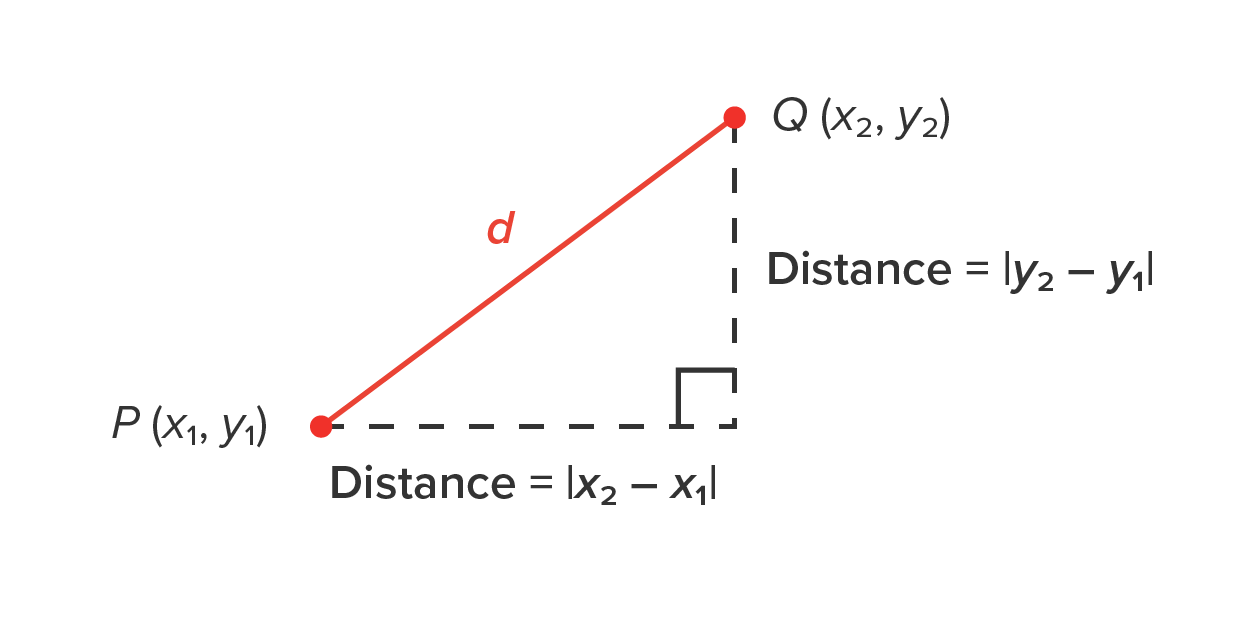
A right-angled triangle with its longest side connecting two marked points. The first point is labeled P (x1, y1), and the second point is labeled Q(x2, y2). The vertical side of the triangle is labeled ‘Distance equals absolute value of y2 – y1'. The horizontal side of the triangle is labeled ‘Distance equals absolute value of x2 – x1'. The longest side is labeled 'd'.

In the image above:

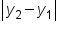  • The vertical side is the distance between the y-coordinates, which is open vertical bar y subscript 2 minus y subscript 1 close vertical bar.
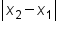  • The horizontal side is the distance between the x-coordinates, which is open vertical bar x subscript 2 minus x subscript 1 close vertical bar.
  • The distance between the points is labeled as d.
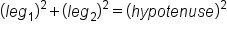Notice that we have three sides of a right triangle. This means that the Pythagorean theorem can be used to relate the sides to each other. Recall that the Pythagorean theorem states that open parentheses l e g subscript 1 close parentheses squared plus open parentheses l e g subscript 2 close parentheses squared equals open parentheses h y p o t e n u s e close parentheses squared, where a leg is defined as a side that makes up the right angle and the hypotenuse is the side opposite the right angle (the longest side).

Applying the Pythagorean theorem to our image, we have 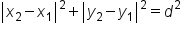open vertical bar x subscript 2 minus x subscript 1 close vertical bar squared plus open vertical bar y subscript 2 minus y subscript 1 close vertical bar squared equals d squared.

hint
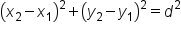Notice that the first two terms are squares of absolute values. Since squaring also guarantees a nonnegative result, there is no need to include the absolute value. Thus, the relationship actually can be rewritten as open parentheses x subscript 2 minus x subscript 1 close parentheses squared plus open parentheses y subscript 2 minus y subscript 1 close parentheses squared equals d squared.

To write an expression for the distance, d, take the square root of both sides to get the following formula:

formula to know
Distance in the xy-Plane
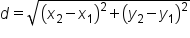
d equals square root of open parentheses x subscript 2 minus x subscript 1 close parentheses squared plus open parentheses y subscript 2 minus y subscript 1 close parentheses squared end root

hint
You might remember from algebra that taking the square root of both sides results in a positive solution and a negative solution. Since distance is always nonnegative, only the positive square root is considered.

EXAMPLE

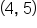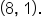
Calculate the exact distance between the points open parentheses 4 comma space 5 close parentheses and open parentheses 8 comma space 1 close parentheses.

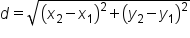
d equals square root of open parentheses x subscript 2 minus x subscript 1 close parentheses squared plus open parentheses y subscript 2 minus y subscript 1 close parentheses squared end root Distance Formula
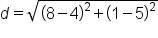
d equals square root of open parentheses 8 minus 4 close parentheses squared plus open parentheses 1 minus 5 close parentheses squared end root Substitute known quantities: 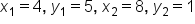x subscript 1 equals 4 comma space y subscript 1 equals 5 comma space x subscript 2 equals 8 comma space y subscript 2 equals 1.
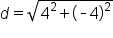
d equals square root of 4 squared plus open parentheses short dash 4 close parentheses squared end root Evaluate subtraction inside parentheses.
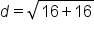
d equals square root of 16 plus 16 end root Square values.
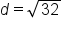
d equals square root of 32 Add values under the square root.
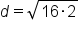
d equals square root of 16 times 2 end root Rewrite the square root with any perfect square factors.
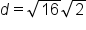
d equals square root of 16 square root of 2 Apply the product property of square roots.
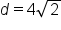
d equals 4 square root of 2 Simplify the radical.

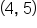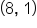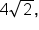The distance between the points open parentheses 4 comma space 5 close parentheses and open parentheses 8 comma space 1 close parentheses is 4 square root of 2 comma or about 5.66 units.

watch
The following video further illustrates the use of the distance formula.

summary
In this lesson, you learned how to calculate the distance between two numbers on a number line by calculating the absolute value of their difference. Next, you applied this idea, along with the Pythagorean theorem, to arrive at the distance formula to calculate the distance between two points in the xy-plane.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Distance

The length of a line segment between two points.

Formulas to Know
Distance in the xy-Plane

d equals square root of open parentheses x subscript 2 minus x subscript 1 close parentheses squared plus open parentheses y subscript 2 minus y subscript 1 close parentheses squared end root

Distance on a Number Line

d i s t open parentheses a comma b close parentheses equals open vertical bar b minus a close vertical bar

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.