Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Determining Differentiability Graphically

Author: Sophia
PDF Version

what's covered
In this lesson, you will look at what causes a function to not be differentiable and use graphical reasoning to determine differentiability, which is more straightforward than the analytical approach. Specifically, this lesson will cover:

Table of Contents

1. Discontinuities

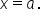
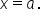
As discussed in the previous section, a function is not differentiable at x equals a if it is discontinuous at x equals a.

big idea
Therefore, if there is a break in the graph when x equals a, the function is not differentiable at x equals a.

There are three types of discontinuity:

Hole in the Graph Graph Jumps Vertical Asymptote
A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10. A parabolic curve descends from the second quadrant, opens upward from the origin, and extends into the first quadrant by passing through an open circle at (1.3, 2.3). The open circle represents a hole in the graph. A graph with an x-axis and a y-axis ranging from −6 to 6. The graph consists of two lines with a restricted domain representing a graph jump. A line begins at a closed dot at (1, −1) in the fourth quadrant and slants upward into the first quadrant by crossing the x-axis between 1 and 2. The second line slants upward from the third quadrant and ends at an open circle at (1, 1) by crossing the origin. A graph with an x-axis and a y-axis ranging from −6 to 6. The graph has two curves. One curve begins along the negative x-axis in the third quadrant and opens downward, extending into the fourth quadrant by crossing the y-axis between 0 and −1, then decreasing sharply toward the vertical line x equals 2. Another curve begins in the upper part of the first quadrant to the right of the vertical line x equals 2 and decreases sharply at first, then approaching the positive x-axis in the first quadrant. A vertical dashed line passes through the point (2, 0), representing a vertical asymptote at x equals 2.

Since the continuity requirement isn’t met at any discontinuity, it follows that a function is not differentiable at any x-value where f open parentheses x close parentheses is discontinuous.

EXAMPLE

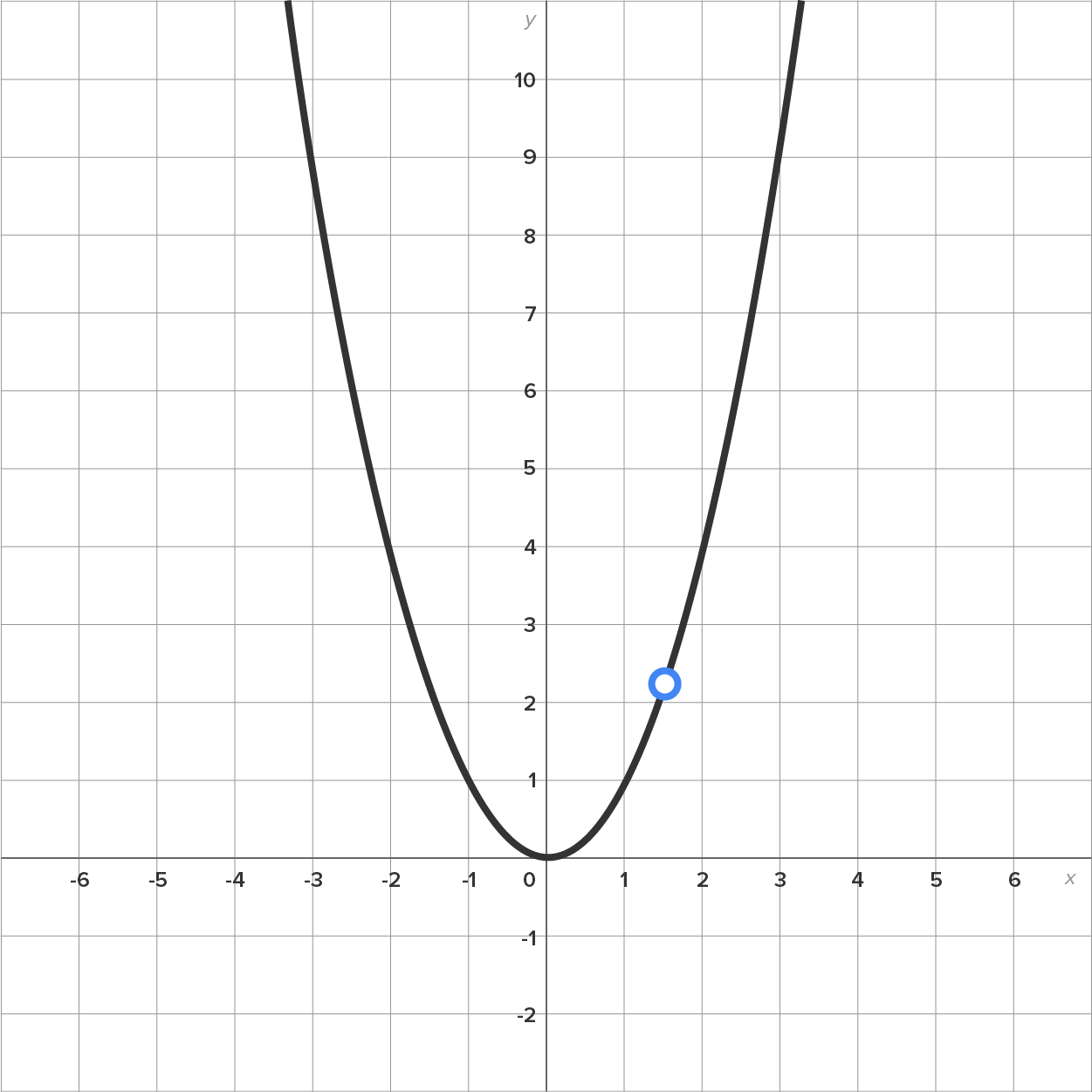
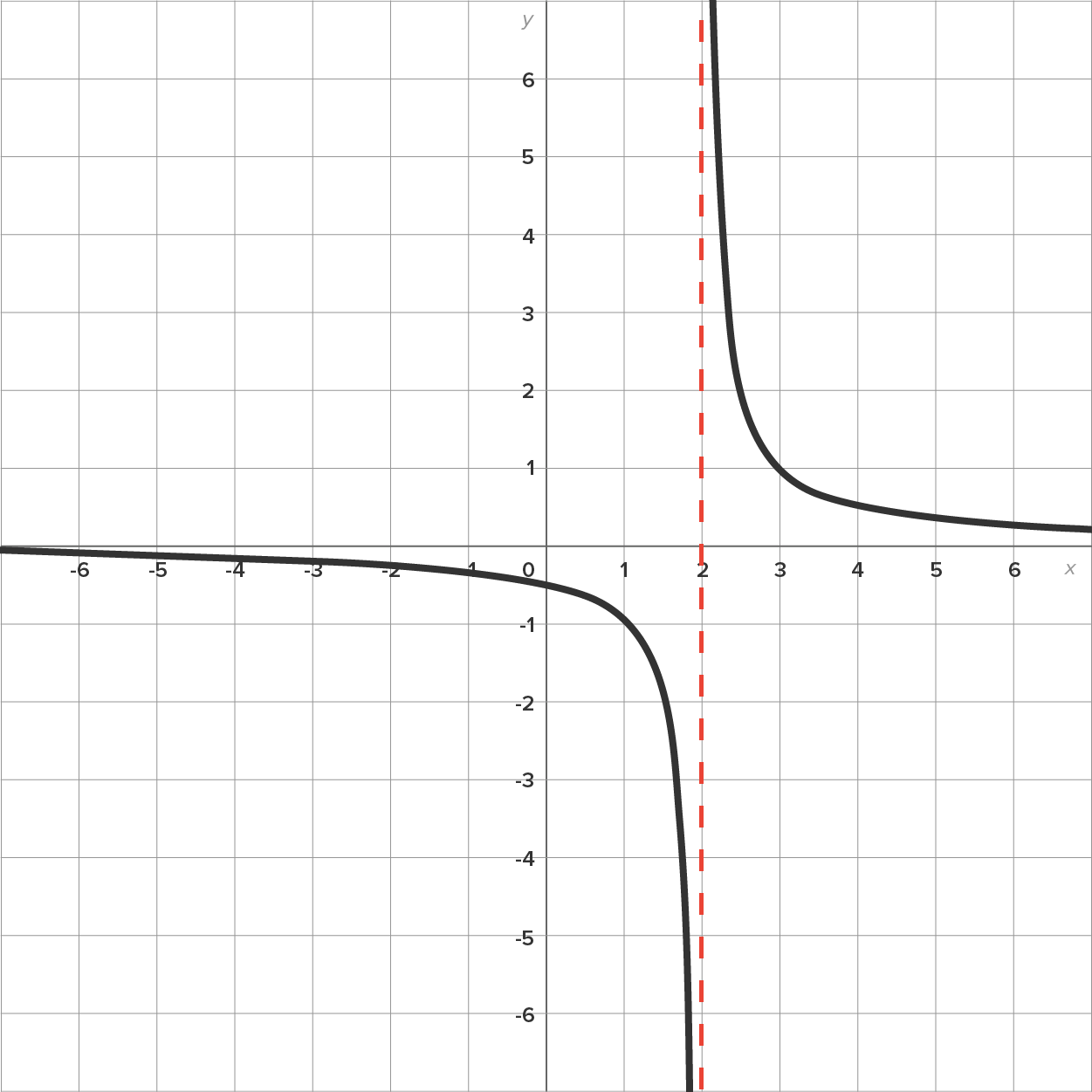
Consider the function f open parentheses x close parentheses equals fraction numerator 3 open parentheses x minus 5 close parentheses open parentheses x plus 2 close parentheses over denominator open parentheses x plus 2 close parentheses open parentheses x minus 4 close parentheses end fraction comma whose graph is shown below.

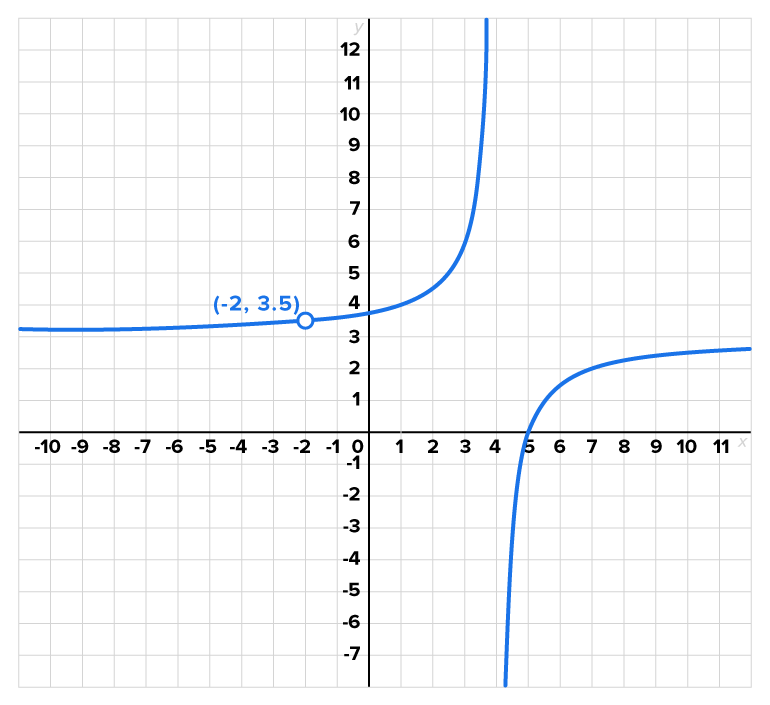
A graph with an x-axis ranging from −10 to 11 and a y-axis ranging from −7 to 12. The graph has two curves. One curve starts from the second quadrant near the point (−10, 3.2), passes through an open circle at (−2, 3.5) and through the point (1, 4), and extends upward in the first quadrant along the left side of the line x equals 4. The second curve starts in the fourth quadrant along the right side of the line x equals 4, passes through the point (4.3, −7), then through the points (5, 0) and (7, 2), and extends to the right in the first quadrant.

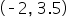The graph has a hole at the point open parentheses short dash 2 comma space 3.5 close parentheses and a vertical asymptote at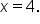 x equals 4.

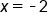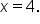
Therefore, f open parentheses x close parentheses is not differentiable when x equals short dash 2 and when x equals 4.

2. Vertical Tangents

When a tangent line is vertical, its slope is undefined. Since the derivative is the slope of a tangent line, a function is not differentiable at any point where there is a vertical tangent line.

EXAMPLE

Consider the graph of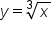 y equals cube root of x, shown below:

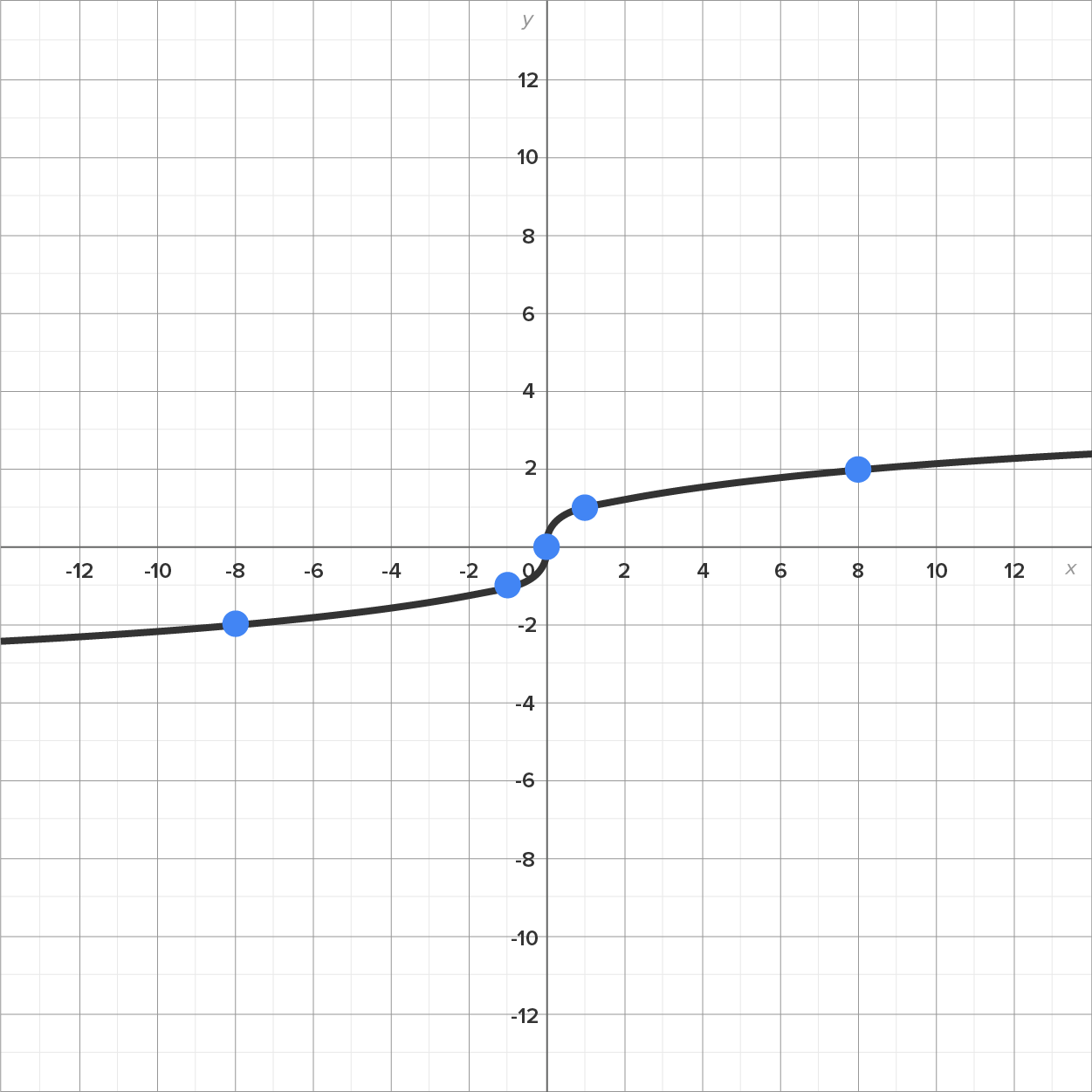
A graph with an x-axis and a y-axis ranging from −12 to 12. A curve begins from the third quadrant; passes through the marked points (−8, −2), (−1, −1), (0, 0), (1, 1), and (8, 2); and extends into the first quadrant. The curve seems to depict a function that increases smoothly and gradually.

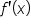Note that when x = 0, the tangent line appears to be vertical. In fact, we can show this by finding f apostrophe open parentheses x close parentheses, which was calculated in 3.2.1: 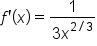f apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator 3 x to the power of 2 divided by 3 end exponent end fraction, which is undefined when x = 0, indicating an undefined slope (vertical line). Recall that in order for a function to be differentiable at a point, the derivative has to be defined at that point. Therefore, a vertical tangent line at a point is an indication that the function is not differentiable at that point.

3. Sharp Corners

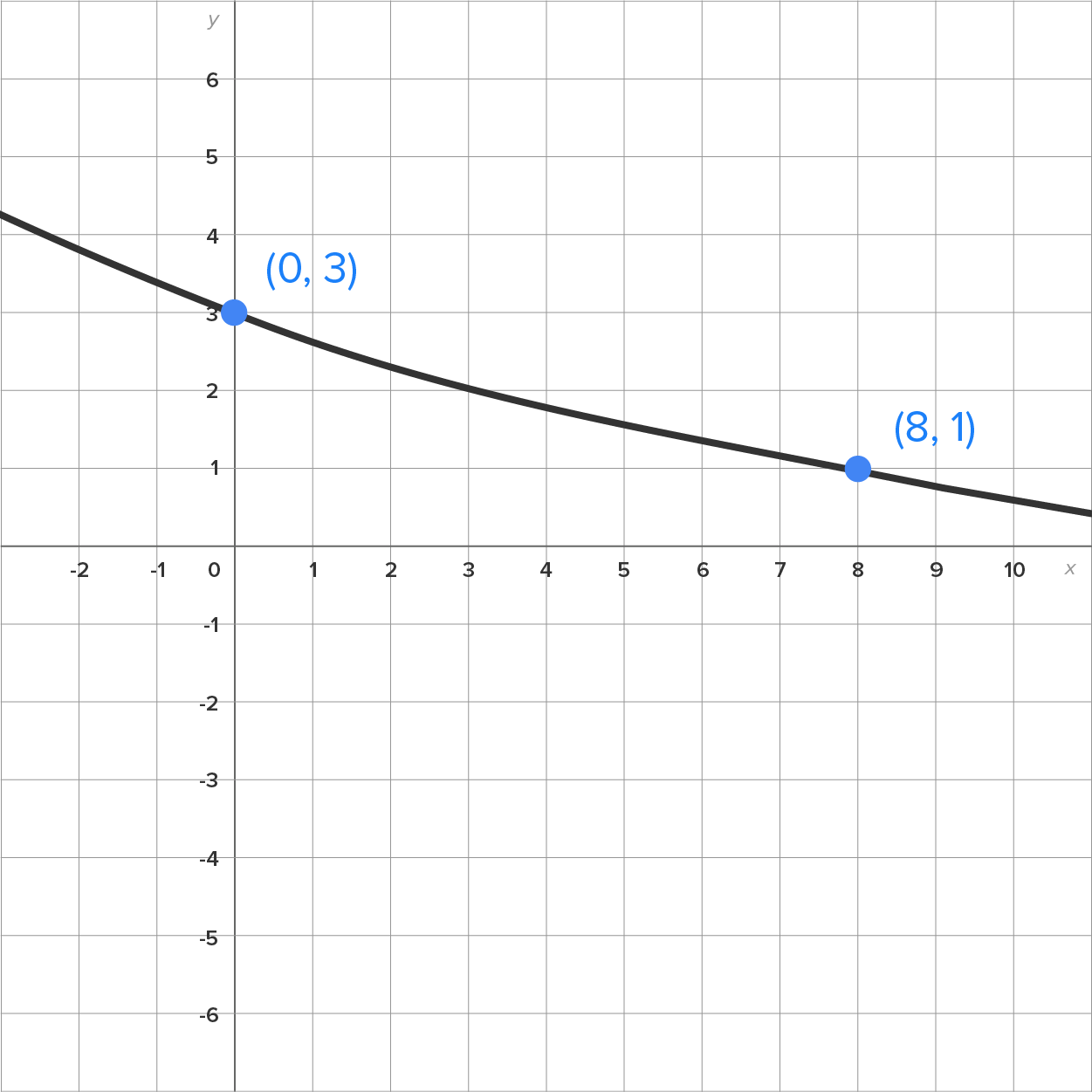
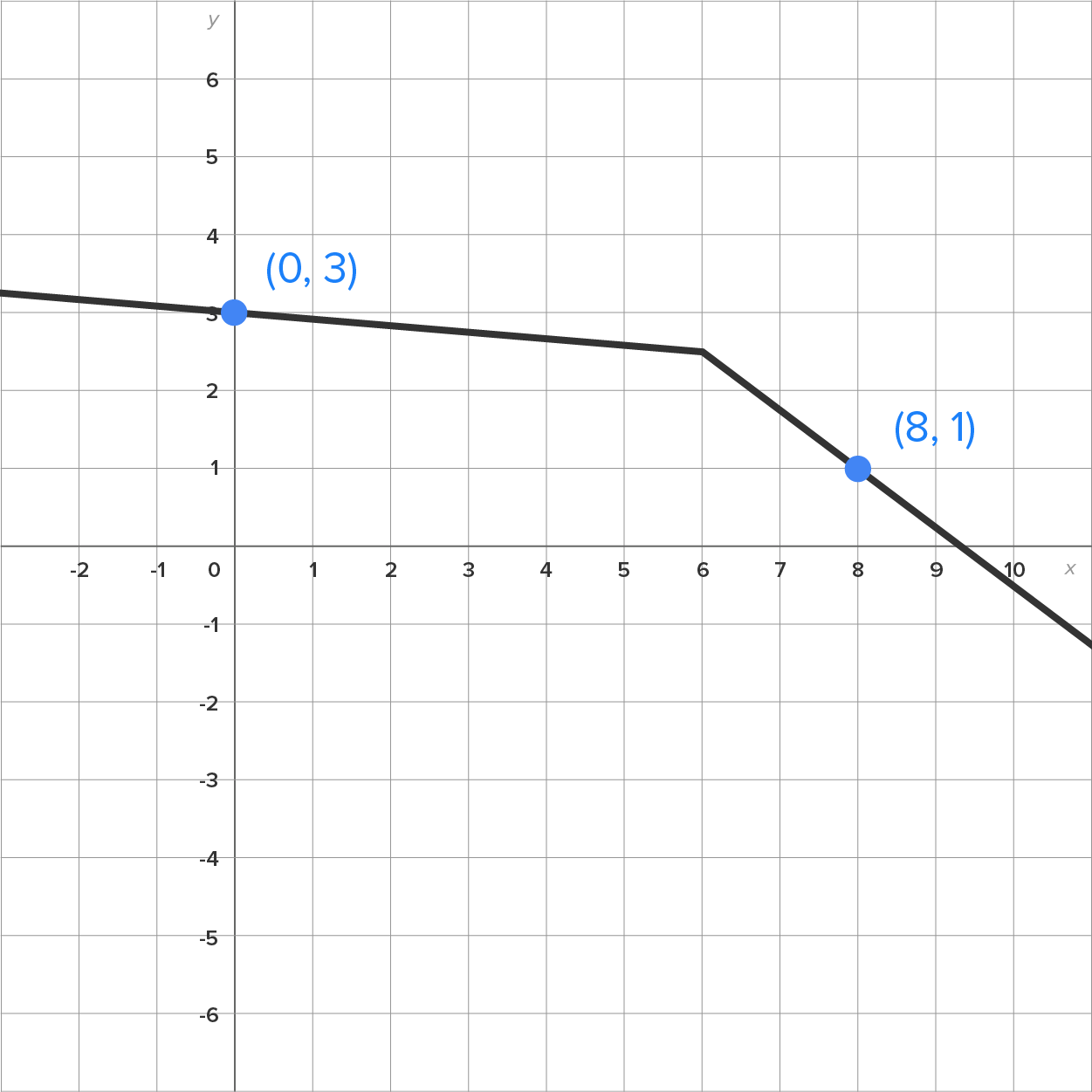
Suppose you want to drive along a road from (0, 3) to (8, 1). Which graph provides a smoother ride?

Graph #1 Graph #2
A graph with an x-axis ranging from −2 to 10 and a y-axis ranging from −6 to 6. A curve extends from the second quadrant to the first quadrant by passing through the marked points at (0, 3) and (8, 1). The graph consists of a smooth, continuous curve that falls gradually from left to right. A graph with an x-axis ranging from −2 to 10 and a y-axis ranging from −6 to 6. A line gently slopes downward from the second quadrant to the first quadrant by passing through a marked point at (0, 3). The line bends sharply downward from x equals 6 and ends at the marked point (8, 1).

Hopefully, you said the first one. The second graph shows a sudden transition (change in slope) when x = 6 (at the sharp corner), while the first graph changes smoothly from start to finish.

big idea
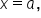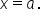When the slope suddenly changes at x equals a comma then we say f open parentheses x close parentheses is not differentiable when x equals a. This is sometimes referred to as a sharp corner.

Thus, the function represented in the second graph is not differentiable when x = 6.

4. Cusps

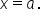We already have seen that a function is not differentiable at x equals a if there is a corner point at x equals a. If the corner point happens to also have undefined slope, then that corner point is called a cusp. A cusp is a special type of corner point in that the slope of the tangent line at the cusp is undefined (vertical tangent line).

EXAMPLE

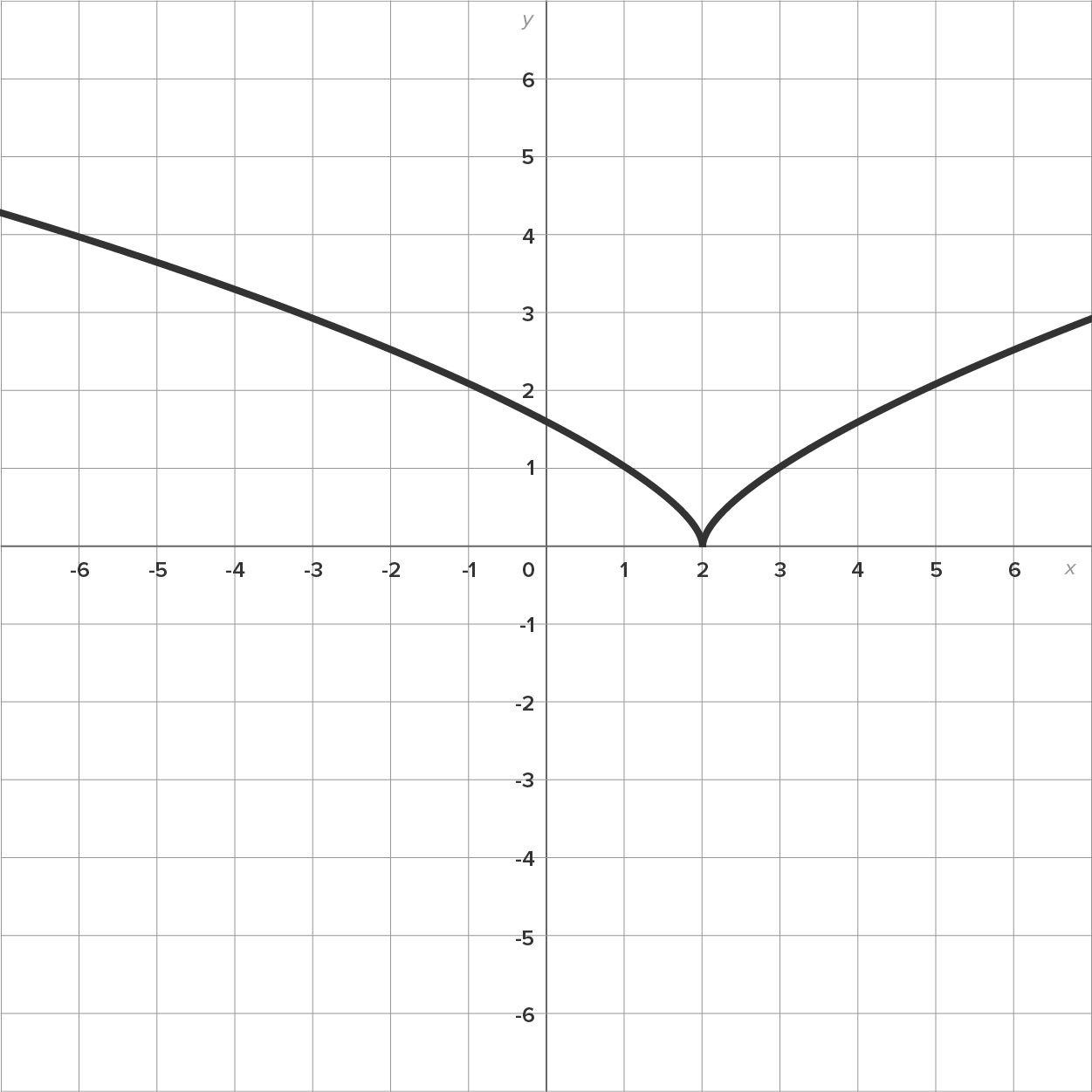
Consider the graph of y equals f open parentheses x close parentheses shown below.

A graph with an x-axis and a y-axis ranging from −6 to 6. The graph has a V-shaped curve, starting from the second quadrant, passing through the points (0, 1.5) and (2, 0), and extending into the first quadrant. It has a sharp vertex at (2, 0) and rises in both quadrants as it moves away from the x-axis.

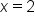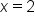This graph shows a sharp corner at x equals 2.

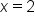Notice that as x gets closer to 2 from either side, the slope gets steeper and steeper until becoming vertical. This implies that the derivative at x equals 2 is undefined, meaning that this function is not differentiable when x equals 2.

Since the tangent line is vertical at this point, we call this point a cusp.

think about it
Imagine you are riding on a roller coaster. Obviously you would want the track to be continuous, but on a track full of corner points, the wheels would hit them, resulting in a very bumpy, loud, and dangerous ride.

EXAMPLE

Consider the graph of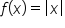 f open parentheses x close parentheses equals open vertical bar x close vertical bar.

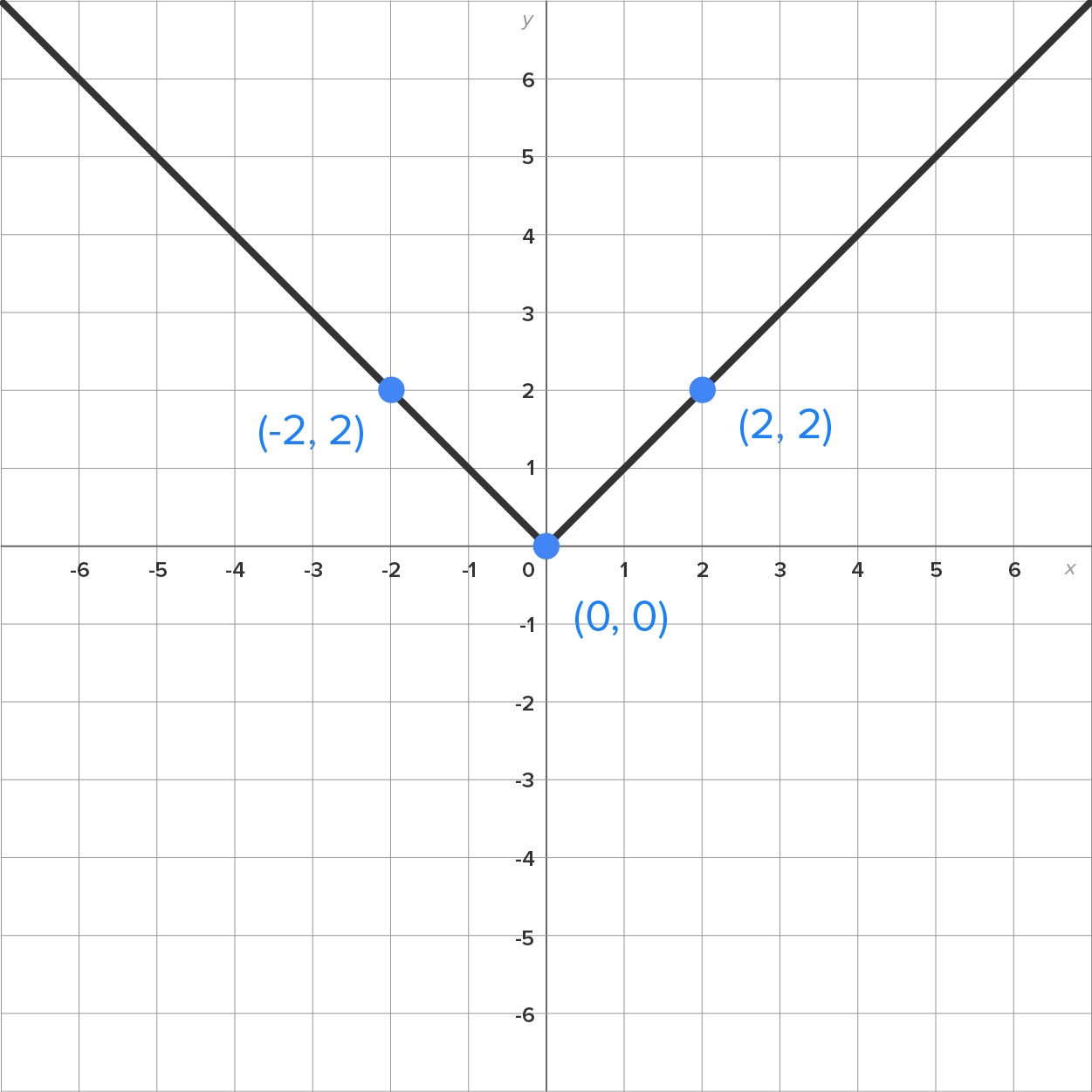
A graph with an x-axis and a y-axis ranging from −6 to 6. A line slants downward from left to right; passes through the marked points (−2, 2), (0, 0), and (2, 2); and extends into the first quadrant, forming a V-shape.

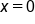Notice that the graph is continuous everywhere (no breaks), but there is a sharp turn when x equals 0. What could this mean? Let’s explore this.

  • To the left of (0, 0), the graph has slope -1.
  • To the right of (0, 0), the graph has slope 1.
  • At (0, 0), the slope changes directly from -1 to 1.
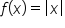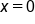Thus, f open parentheses x close parentheses equals open vertical bar x close vertical bar is not differentiable at x equals 0.

try it
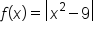Shown below is the graph of f open parentheses x close parentheses equals open vertical bar x squared minus 9 close vertical bar.

A graph with an x-axis and a y-axis ranging from −6 to 6. The graph has a single solid W-shaped parabolic curve. The curve descends from the second quadrant to the point (−3, 0); rises and passes through the marked points (−1, 2.8), (0, 3), and (1, 2.8); and then descends to the point (3, 0). From there, the curve extends upward.

Find all values of x for which f (x) is not differentiable.
Since there are sharp turns at open parentheses short dash 3 comma space 0 close parentheses and open parentheses 3 comma space 0 close parentheses comma the function is not differentiable at x equals 3 and x equals short dash 3.

try it
A graph with a horizontal axis ranging from −1 to 7. The graph consists of two wavy curves, where one curve starts from the left, increasing through a closed dot at x equals −1, somewhere above the x-axis. It then continues to increase before coming to a point around x equals 0, then decreasing sharply, then more gradually until reaching an open circle at x equals 1, then rises again, ending at another open circle at x equals 3. The second curve begins at a closed dot at x equals 3 and ascends steeply until reaching an open circle at x equals 5. From there, the curve drops sharply to an open circle at x equals 6, then rises again toward the right side of the graph.
Using the graph, determine the values of x for which f (x) is not differentiable.
x equals 0 (cusp), 1 (hole), 3 (jump), 5 (hole), 6 (cusp)

term to know
Cusp
A pointed end where two parts of a curve meet at a vertical tangent.

summary
In this lesson, you learned that there are several graphical properties that indicate that a function is not differentiable: discontinuities, vertical tangents, sharp corners, and cusps. These are relatively easy to spot on a graph and therefore make the work of determining differentiability simpler. As you also saw, differentiability is necessary in circumstances in which smooth transitions are important, such as in the track of a roller coaster.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 2 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Cusp

A pointed end where two parts of a curve meet at a vertical tangent.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.