Table of Contents |
Consider the area of the region bounded by 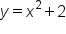 between the x-axis,
between the x-axis, 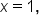 and
and 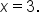
Shown below is the actual region as well as the region approximated by 4, 8, and 16 rectangles; all have equal width.
| Actual Region | 4 Rectangles |
|---|---|
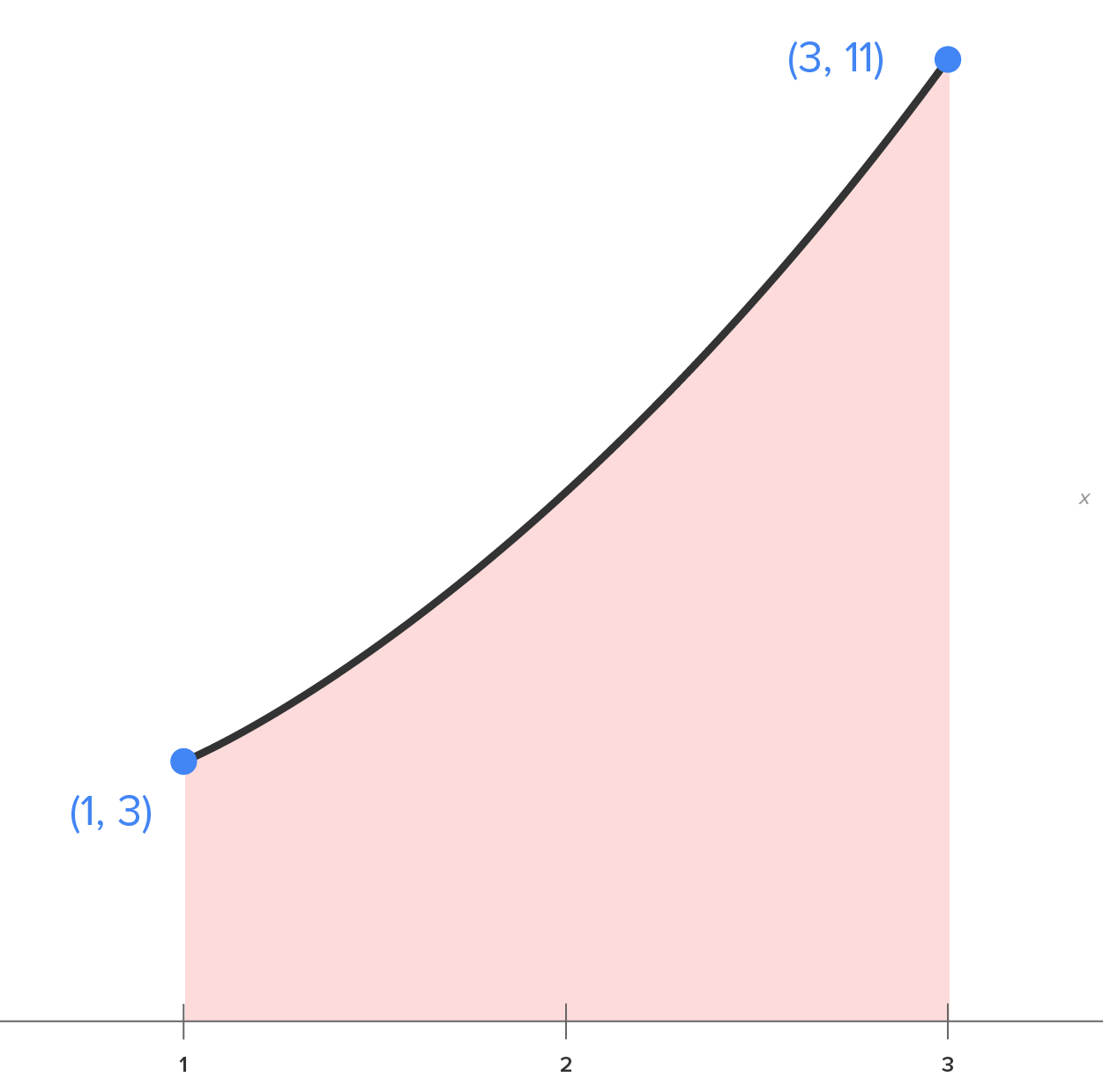
|
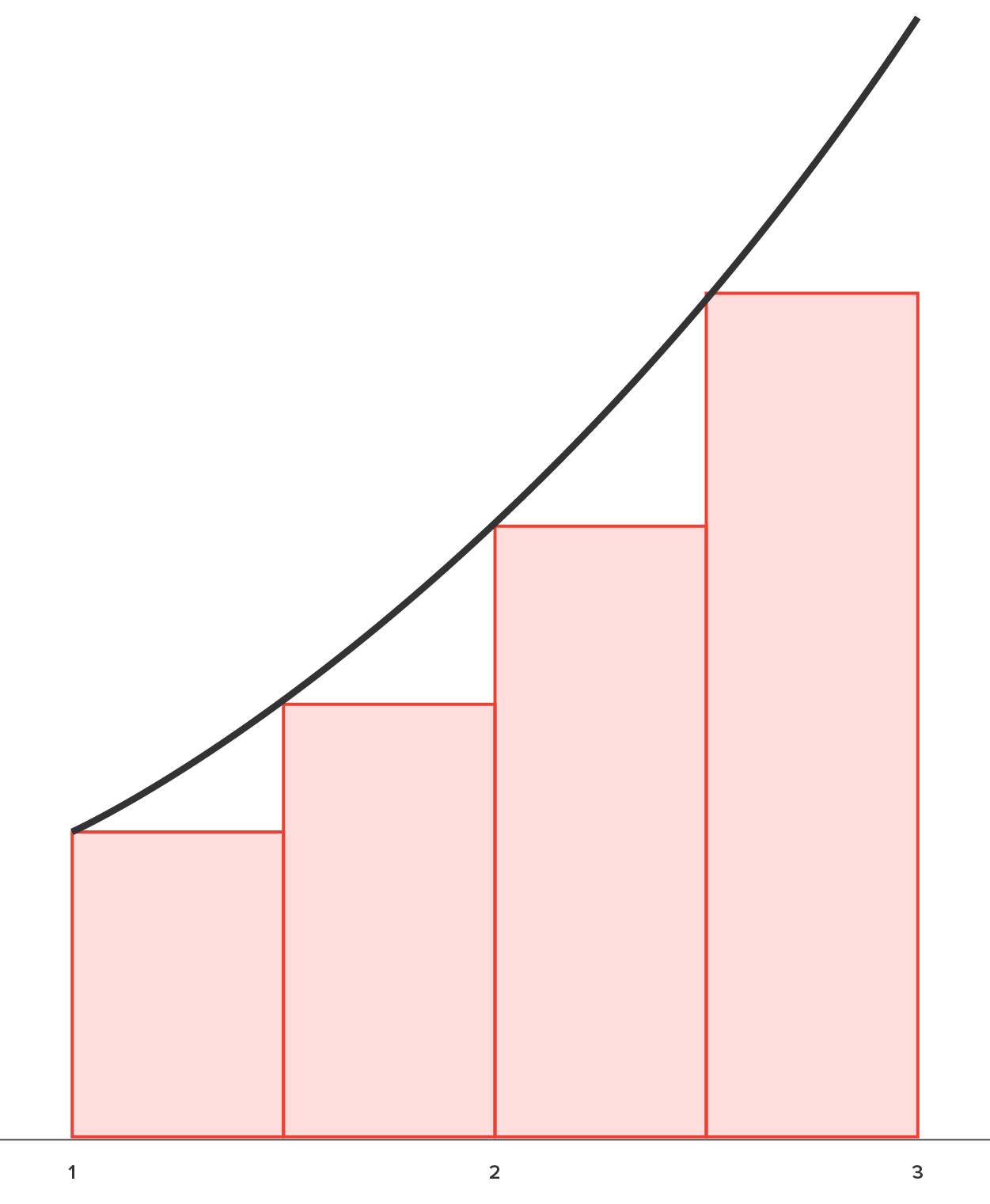
|
| 8 Rectangles | 16 Rectangles |
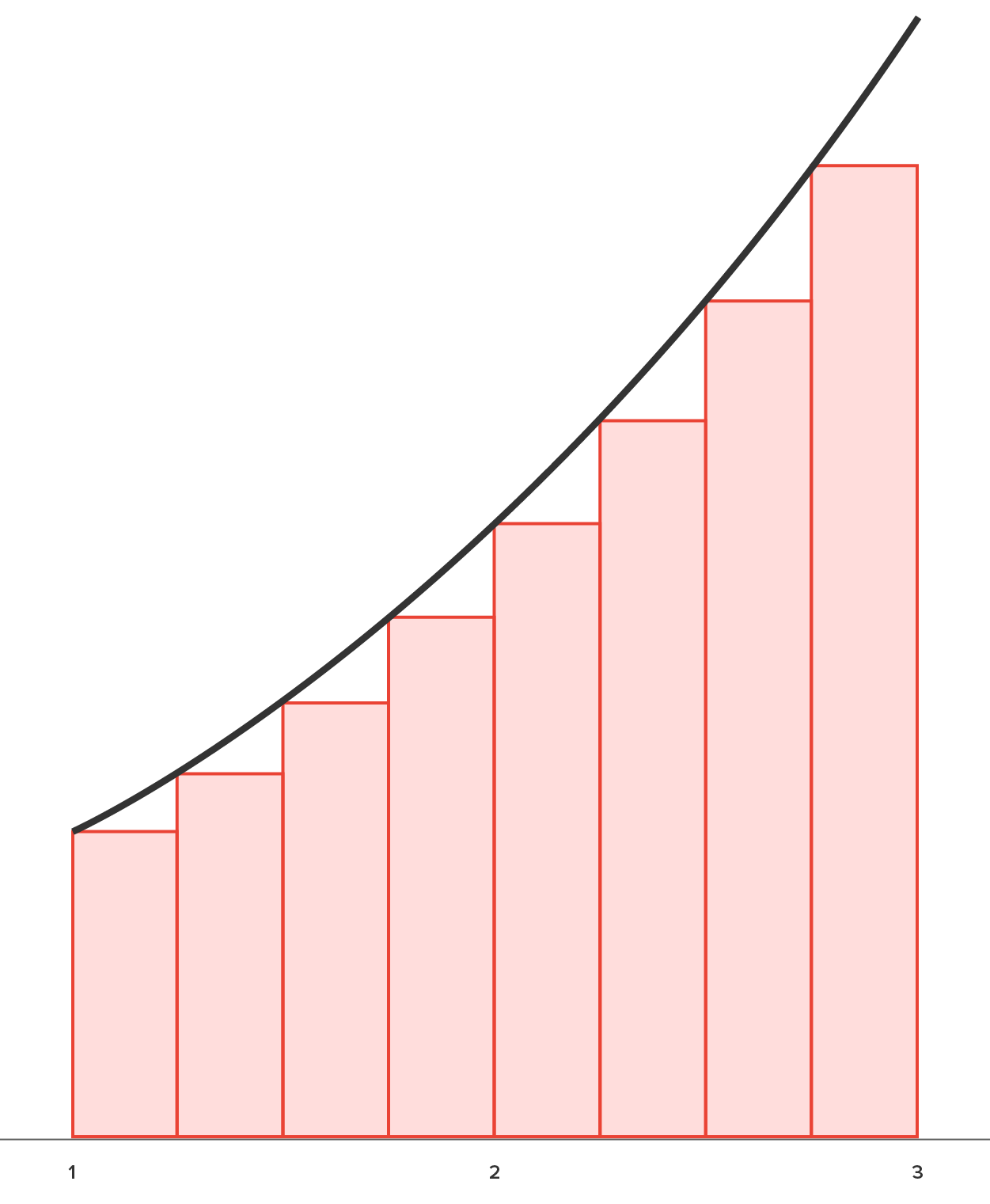
|
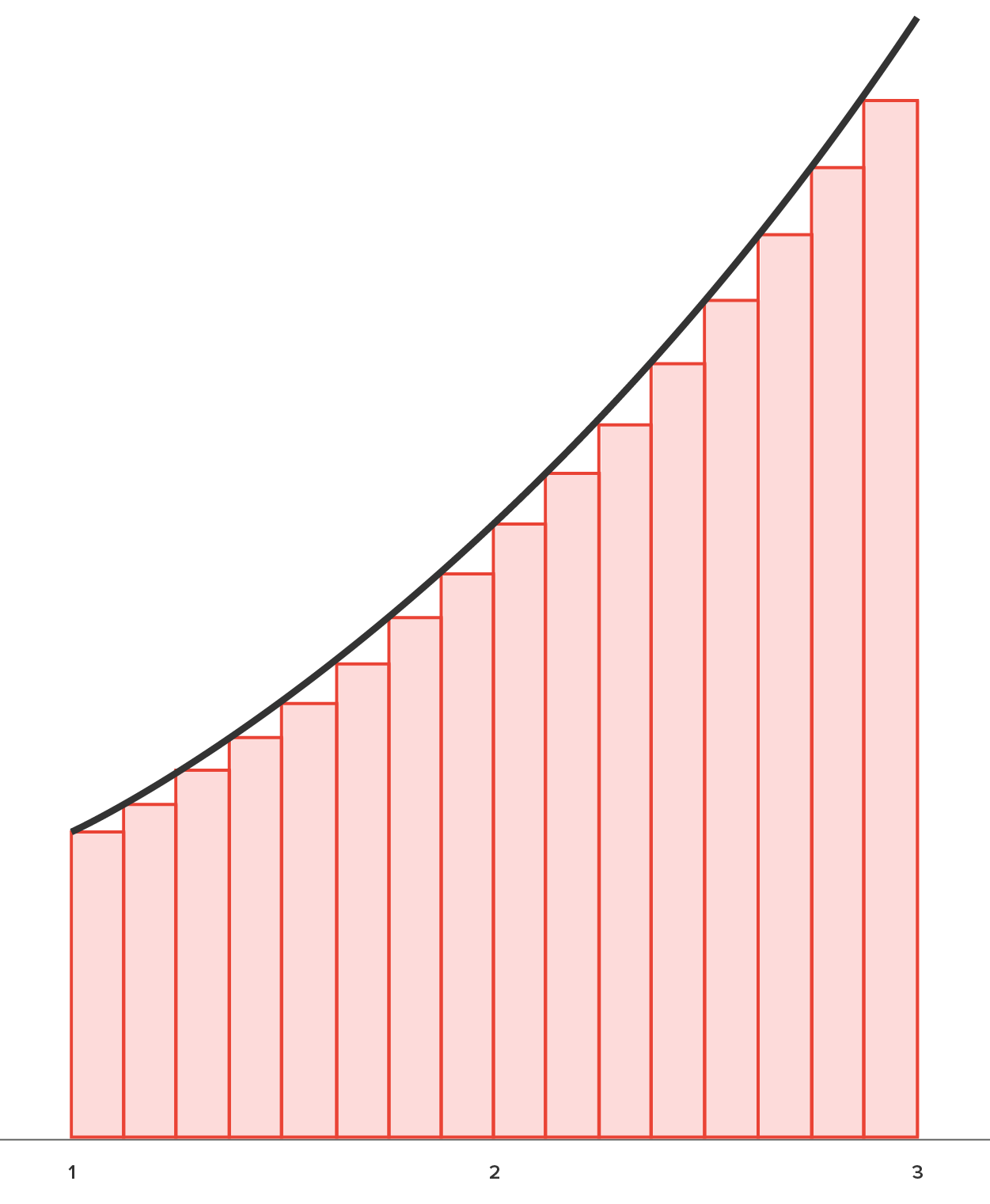
|
When the subintervals have equal width, we notice the following as the number of rectangles (and subintervals) increases:
 on
on 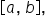 we will only use rectangles that have equal width. That is, when n subintervals are used, the width of each subinterval is
we will only use rectangles that have equal width. That is, when n subintervals are used, the width of each subinterval is 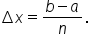 This also means that Riemann sums from this point forward will be written as:
This also means that Riemann sums from this point forward will be written as:
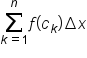
 is nonnegative. As the number of rectangles gets larger, which means that
is nonnegative. As the number of rectangles gets larger, which means that 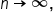 this quantity will get closer to the actual area as long as
this quantity will get closer to the actual area as long as 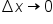 for all k.
for all k.
When 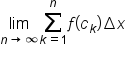 exists and has the same value regardless of the values of
exists and has the same value regardless of the values of 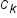 used in each subinterval, then
used in each subinterval, then  is integrable on
is integrable on 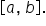
If we call A the definite integral of  on
on 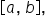 then
then 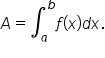
In this notation,
 is called the integrand.
is called the integrand. 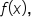 the value of the Riemann sum approaches the definite integral as
the value of the Riemann sum approaches the definite integral as 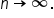 Then, the quantity
Then, the quantity 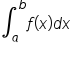 is the area between the graph of a nonnegative function
is the area between the graph of a nonnegative function  and the x-axis, between
and the x-axis, between 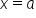 and
and 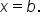
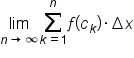 exists and is equal to A regardless of the values of
exists and is equal to A regardless of the values of 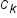 used in each subinterval, then we say that
used in each subinterval, then we say that  is integrable on the interval
is integrable on the interval 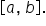
Using the definition of a definite integral, we can write Riemann sums as definite integrals and vice versa.
EXAMPLE
Write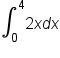 as a Riemann sum.
as a Riemann sum.
 is
is 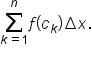
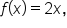 the definite integral is the value of the Riemann sum as
the definite integral is the value of the Riemann sum as 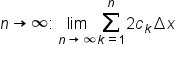
Now, let’s take a Riemann sum and write it as a definite integral.
EXAMPLE
A function on the interval
on the interval 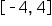 has the Riemann sum
has the Riemann sum 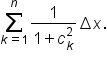
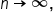 and is written
and is written 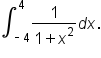
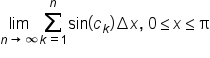
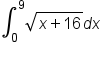
We learned that  is integrable on
is integrable on 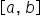 if
if 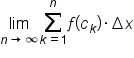 exists and is equal to the same value for any choice of
exists and is equal to the same value for any choice of 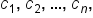 each of which is in their respective subintervals.
each of which is in their respective subintervals.
By using the formulas for sigma notation combined with the limit definition, we can evaluate some definite integrals of functions for which we don’t know the area of the corresponding region.
Here is how:
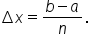
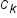 to be the right-hand endpoint of the interval. Then,
to be the right-hand endpoint of the interval. Then, 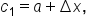
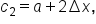
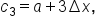 ... which means
... which means 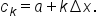
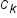 into the function.
into the function. EXAMPLE
Use a Riemann sum to evaluate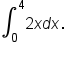
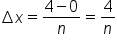
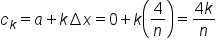
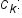
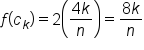
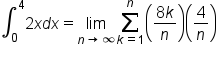 .
.
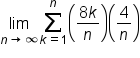
|
Calculate the limit. |
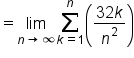
|
Simplify. |
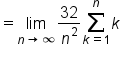
|
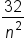 is a constant factor since k is the index of summation. Therefore, it can be factored out. is a constant factor since k is the index of summation. Therefore, it can be factored out.
|
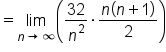
|
Apply the summation formula: 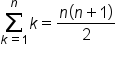
|
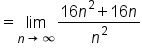
|
Simplify. |
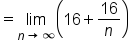
|
Divide each term by 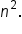
|
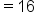
|
Evaluate the limit. |
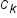 used (left endpoints, etc.), this holds true.
used (left endpoints, etc.), this holds true.
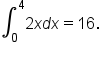
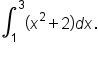
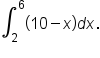
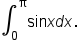 The corresponding limit of a Riemann sum is
The corresponding limit of a Riemann sum is 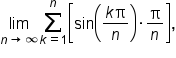 which has no known summation formula. We will learn how to find the value of the definite integral without summations in a future challenge.
which has no known summation formula. We will learn how to find the value of the definite integral without summations in a future challenge.
EXAMPLE
Evaluate the definite integral: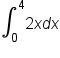
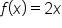 and the x-axis on the interval
and the x-axis on the interval 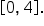
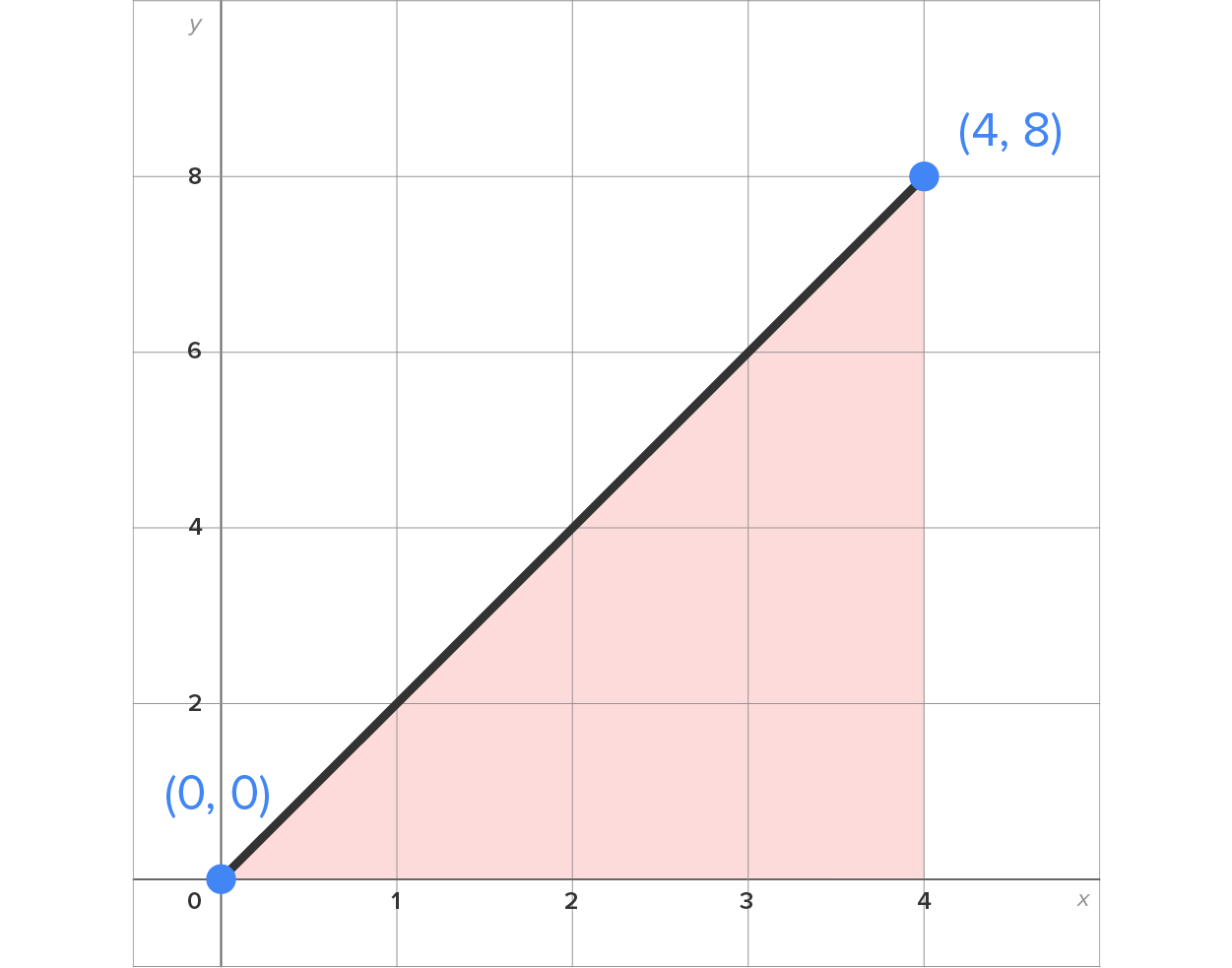
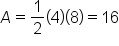 square units.
square units.
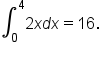
Let’s look at an example of a continuous piecewise function.
EXAMPLE
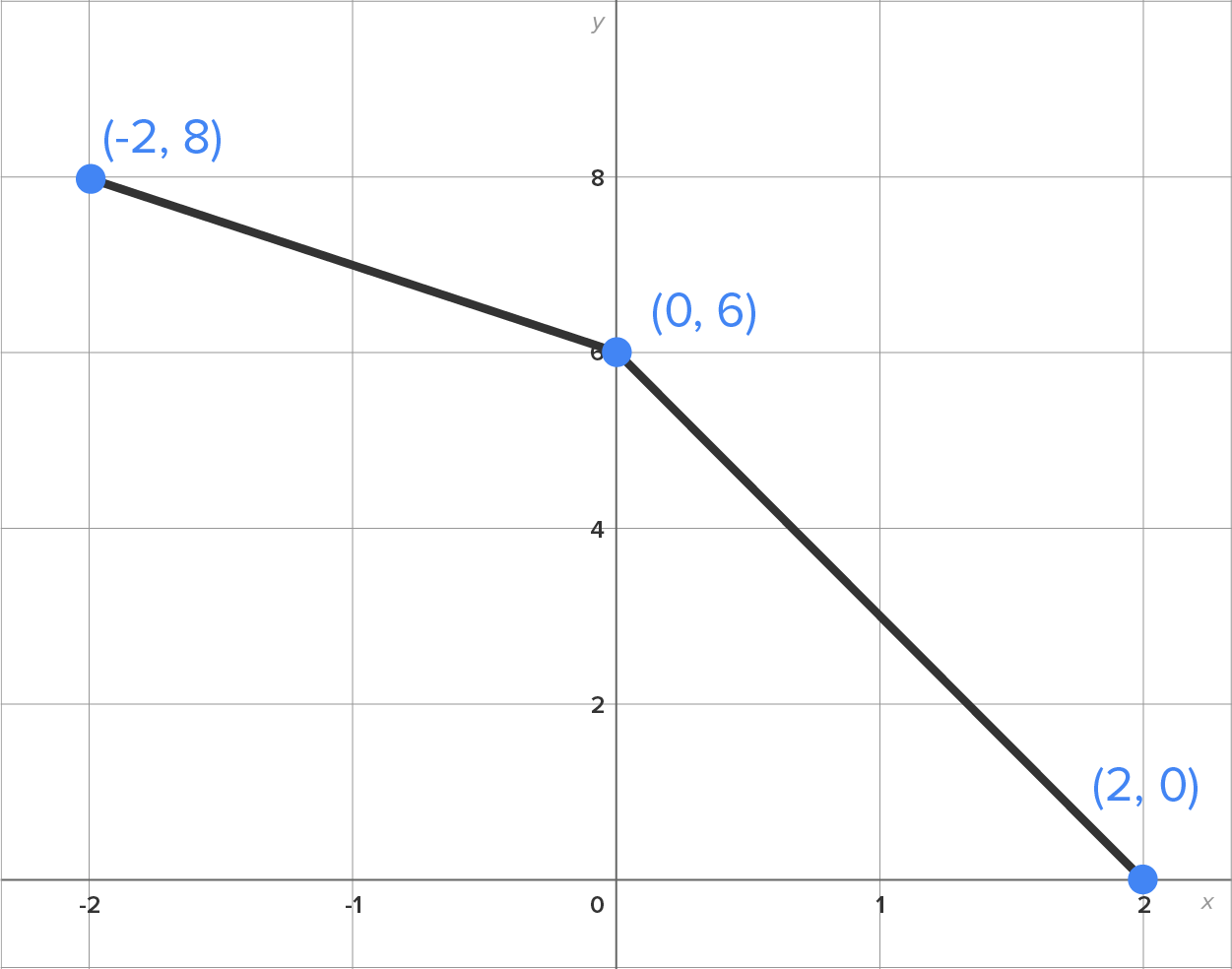
Consider the graph of shown in the figure. Use it to evaluate
shown in the figure. Use it to evaluate 
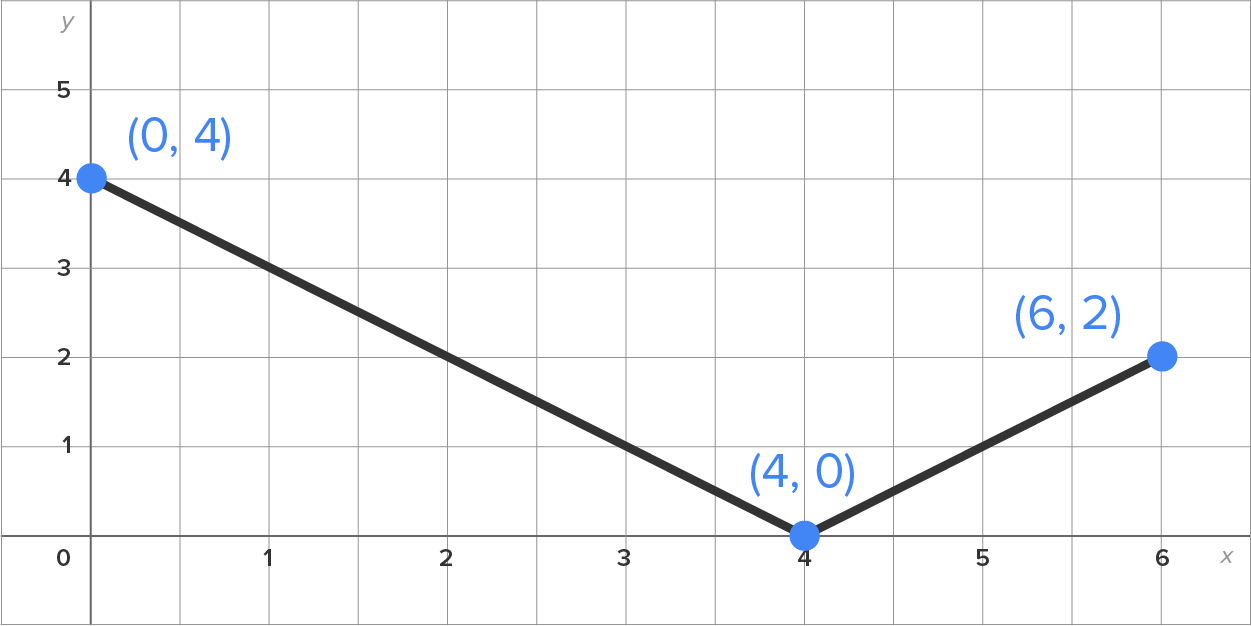
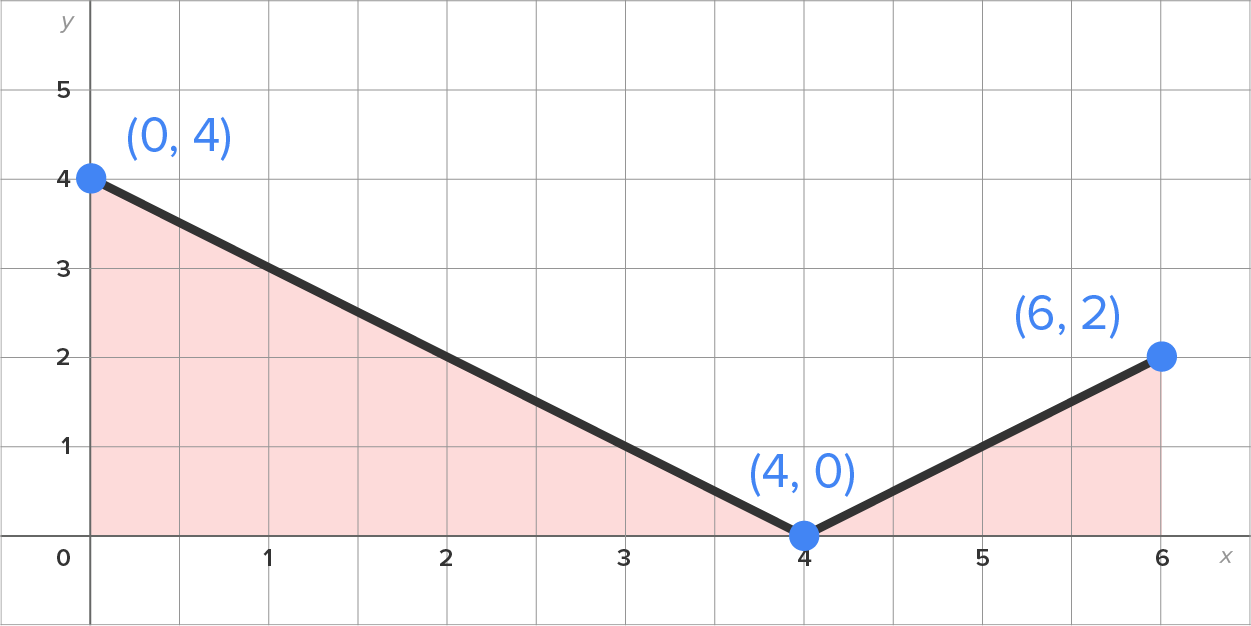
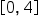 has area
has area 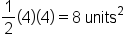 and the triangle on
and the triangle on 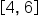 has area
has area 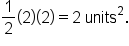
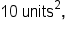 which means that
which means that 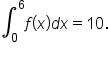
 shown in the figure that can be used to evaluate
shown in the figure that can be used to evaluate 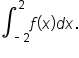
As it turns out,  doesn't have to be continuous in order to be integrable. Here is an example that illustrates this.
doesn't have to be continuous in order to be integrable. Here is an example that illustrates this.
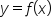 shown to evaluate
shown to evaluate 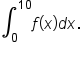
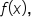 the value of the Riemann sum approaches the definite integral as
the value of the Riemann sum approaches the definite integral as 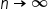 . You also learned that by using the formulas for sigma notation combined with the limit definition, you can evaluate definite integrals of functions for which you don’t know the area of the corresponding region, by using Riemann sums to visualize how the area between
. You also learned that by using the formulas for sigma notation combined with the limit definition, you can evaluate definite integrals of functions for which you don’t know the area of the corresponding region, by using Riemann sums to visualize how the area between  and the x-axis on
and the x-axis on 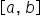 is obtained. Finally, through a series of examples using area to evaluate Riemann sums and definite integrals, you have seen that
is obtained. Finally, through a series of examples using area to evaluate Riemann sums and definite integrals, you have seen that  does not have to be continuous to be integrable.
does not have to be continuous to be integrable.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.